冒泡排序
引用了文章 https://blog.csdn.net/k_koris/article/details/80508543
LeetCode 912题
冒泡排序学了很多次,但是每次都记不住
记不住的可能原因:1.没真正学会 2.没有留下记录
所以博客记录一下冒泡排序的学习过程,从而发现问题。
LeetCode 912题 题目要求
给你一个整数数组 nums,请你将该数组升序排列。
示例 1:
输入:nums = [5,2,3,1]
输出:[1,2,3,5]
示例 2:
输入:nums = [5,1,1,2,0,0]
输出:[0,0,1,1,2,5]
首先注意到,排序是在数组中进行的
数组的特性(相对于链表):插入数据和删除数据效率低,随机读取效率很高
刚好在网上找到一个很好的例子:
- 1、数组中查询: 10个人排成一排,身上都贴好了编号(比如1~10), 你点名喊:“4号”,4号立刻就会站出来, 喊:“8号”,8号立刻就会站出来, 因为大家身上都有编号,知道哪个号对应哪个人
- 2、链表中查询: 10个人手拉手站成一排,但是没有编号,每个人只知道自己的前一个人和后一个人是谁 你点名喊:“4号”,会从第一个人开始依次报数:“1”、“2”、“3”、“4”, 报到“4”的人才会知道自己是4号,才能站出来 所以,按指定位置查询时链表会比数据慢一些
但是链表的插入/删除效率要高于数组: - 3、数组中插入: 10个人排成一排,身上都贴好了编号(比如1~10) 你现在想让一个人插入进入,排在 3 的位置 此时需要做什么呢?需要从3号开始,把每个人身上的编号撕下来, “3号”编号牌交给新来的,“4号”编号牌交给原来的“3号”…… 依次直到最后一个人,还要给他做一个新的编号牌:“11号”
- 4、链表中插入: 10个人手拉手站成一排,但是没有编号,每个人只知道自己的前一个人和后一个人是谁 你现在想让一个人插入进入,排在 3 的位置 此时开始报数,报到“3”的人和前一个人(“2”)松开手, 然后新来的人站进去和原来的“2”位置“3”位置的人拉上手,这三人再看一眼记住自己前后的人是谁, OK 链表的插入过程显然比数组中插入要简便的多.
在学习数组排序之前,我已经知道的4种排序方法:
- 1.冒泡排序
- 2.选择排序
- 3.插入排序
- 4.快速排序
我要结合数组的特性,比较这四种排序的区别,才能加深自己的记忆
选择排序
现实中的选择排序和计算机中的选择排序:
假设有写有110的十张纸张,要求进行升序排序,那么在现实中,我们会直接将写有1的纸张放到最前面,再将写有2的纸张放到“1”纸张后面,以此类推。这种排序方法上述的选择排序比较类似。但是计算机选择排序和我们人肉选择排序有着根本的不同。人肉选择排序是这样比较数字的:比较位数->位数一样比较最大位上的数字->最大位上的数组一样再比较次位上的数字,而且人脑可以同时对多个数进行比较,选出最大/小的一位,例如面对010的数字,人眼可以马上就分出哪个数字最大,哪个最小(一次遍历同时比较十个数字)。
但是计算机在比较数字上面有着一定的“缺陷”:计算机一次只可以比较两个数字,所以要想找到最大/最小的一个数字,我们需要比较第一个和第二个数字,将较大的数字存放进temp(缓存)仲,再用temp和第三个数比较,将较大的数字存放进temp(缓存)中,依次类推,直到temp和最后一个数字比较完才能找出最大/小的数,然后将这个数跟数组的第一个数交换。然后忽略掉第一个已经排序好的数组,用相同的方法找出第2~10个数字中最大/小的一个。
可以看出,计算机中的选择排序有两层遍历(循环),我们要分清哪个是外层,哪个是内层。
外层循环和内层循环的区别:外层循环执行一次,内层循环执行一轮
很明显:外层循环是读取第一个元素,读取第二个元素...读取第n个元素。
内层循环是将外层循环读取的第n个元素和n+1个元素比较,较大者存入temp
temp再和第n+2个元素比较,较大者存入temp,temp再和第n+3个元素比较,较大者存入temp,
一直比较到最后一个元素,最后找出最大的元素,和第n个元素换位
理解一个重点:
-
- 理解外层循环和内层循环的区别(外层循环执行一次,内层循环执行一轮)
选择排序实现
class Solution {
public int[] sortArray(int[] nums) {
for(int i = 0; i<nums.length; i++){
int maxIndex = i;
for(int j = i+1; j<nums.length;j++){
if(nums[j]<=nums[maxIndex]){
maxIndex = j;
}
}
int temp = nums[i];
nums[i] = nums[maxIndex];
nums[maxIndex] = temp;
}
return nums;
}
}
冒泡排序
想象一个升序的10张纸片,上面分别写有1~10,要把它按降序排列。我们可以用第一张纸片和第二张比较,如果第二张比第一张小则交换这两张。再拿第二张纸片和第三张比较,如果第三张较小则交换这两张。。。从结果上来说,我们第一次将最大的纸片放到的最后面,第二次将次大的纸片放到了倒入第二的位置。。。从本质上来讲,这是和选择排序相同的,但是我们没有使用额外的空间来存储temp。也就是说我们通过每次比较之后的交换(选择排序每次只交换一次),使得数组中的一个元素成为了缓存,同时没有改变数组的原有元素(或者说只改变了顺序),可以看作是一种时间(更多的比较)换空间(无需新增缓存空间)。
由于没有了缓冲区,寻找最大值的时候,需要将1,2号元素比较,较大存2;2,3号元素比较,较大存3;n,n+1号元素存n+1,较大值存n+1。所以比较完之后,最大值必然在n+1位置上。在升序排列中,我们一般的做法是找最大值放后面,而不是找最小值放前面。
理解几个重点:
- 1.理解冒泡排序和选择排序的区别(temp)
- 2.利用内层循环比较12,23....nn+1号元素,最后最大值放在n+1上
- 3.在升序排列中,我们一般的做法是找最大值放后面,而不是找最小值放前面
- 4.前面几个重点是有关系的,由于1所以我们要用2的做法,由于2的做法导致了3的结果
之后写冒泡排序应该没问题了。
冒泡排序实现
class Solution {
public int[] sortArray(int[] nums) {
int length = nums.length;
for(int i=0;i<=length;length--){
for(int j=i;j<length-1;j++){
if(nums[j+1]<=nums[j]){
swap(nums[j+1],nums[j]);
}
}
}
return nums;
}
}
归并排序
因为看讲解知道了了快速排序是归并排序的优化版,所以感觉先看归并排序会简单一点。
归并排序思路:
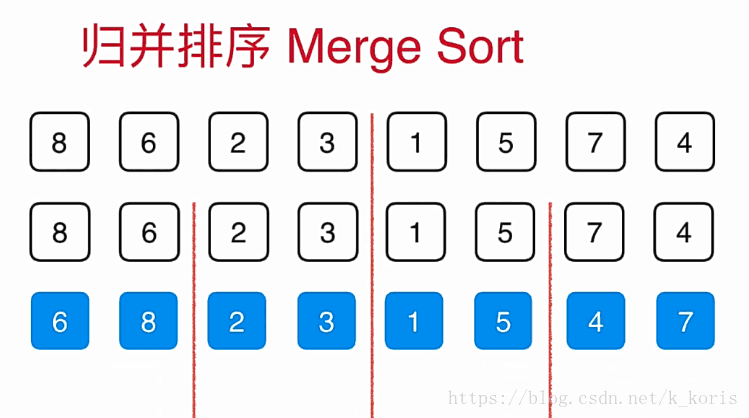
分到一定细度的时候,每一个部分就只有一个元素了,那么我们此时不用排序,对他们进行一次简单的归并就好了。
即使我的算法很烂,也可以看出来这个可以使用递归来实现,因为大的问题可以看作小的问题的集合,且大的问题和小的问题解决方法是一样的,但是这个递归怎么写让我很是头疼。
写递归最重要的是:
1.确定递归函数的作用:可以将两个已排序好的数组进行归并
这里有一个问题,我直接将函数作用定义为“对一个数组进行归并排序并且返回已排序好的数组”,那我是不是什么都不用写,就写一条调用就行了?
答案肯定是不可行的,由此我们也知道使用递归是有条件的,也可以讲能用递归来解决的问题是有条件的:
- 可以通过递归调用来缩小问题规模,且新问题与原问题有着相同的形式。
- 存在一种简单情境,可以使递归在简单情境下退出。
上面的那个问题没有满足第一个条件,因此不可行。
那我可以这样定义吗:定义一个递归函数,作用是将分开一半,并且对生成的两个数组进行排序,合并两个排序好的数组并返回。
2.确定递归函数的边界:数组内元素仅有两个
当然还要考虑到特殊情况:数组内没有有元素或有一个元素
想了好几天都没有思路(1.不知道我上面的思路是否正确,2.不知道答案中temp数组存在的意义)
于是去leetcode看答案去了:https://leetcode-cn.com/problems/sort-an-array/solution/pai-xu-shu-zu-by-leetcode-solution/
发现我的思路大体正确,但是没有落实细节,例如如何拆分数组。
leetcode中的答案根据数组特性,使用下标对数组进行拆分。
temp数组存在的意义是对两个已排序的数组进行合并,没有理解temp是因为之前我认为合并的两个有序数组是这样的:[1,2,3,4],[5,6,7,8],实际上是这样的:[1,5,7,9],[2,3,6,10],所以需要用两个指针跟踪两个数组,比较最前面的元素,比较小的放进temp数组。
可以讲我的思路只想到了mergeSort(),但是没有思考到细节,无法确定mergeSort()应该传入什么参数。
TIP:不深入细节光想是无法验证自己的思路是否正确的~
想通了之后试着开始实现







 浙公网安备 33010602011771号
浙公网安备 33010602011771号