考研红黑树详解

红黑树

　　在考研来讲，红黑树（RBT）其实是平衡二叉树（AVL）的升级化，最显著的优点在于，二叉树是两子树差小于2，而红黑树是二倍关心，所以平衡更不易被打破

那么他肯定是二叉排序树（BST），具备 ：左子树<根<右

以下所有说法，摘自王道考研网课

---

　　复杂度上来看，并没有明显变化

　　红黑树的定义

• 1.每个结点要么红，要么黑
• 2.根结点是黑色的，叶节点也是黑色的（NULL节点）
• 3.不存在两个相邻的红色
• 4.从根到每个叶结点的黑子树数量是相同的

　　王道📕上给了个口诀： 

　　也很好理解

 

　　所以第一个问题，下面哪个是红黑树

 

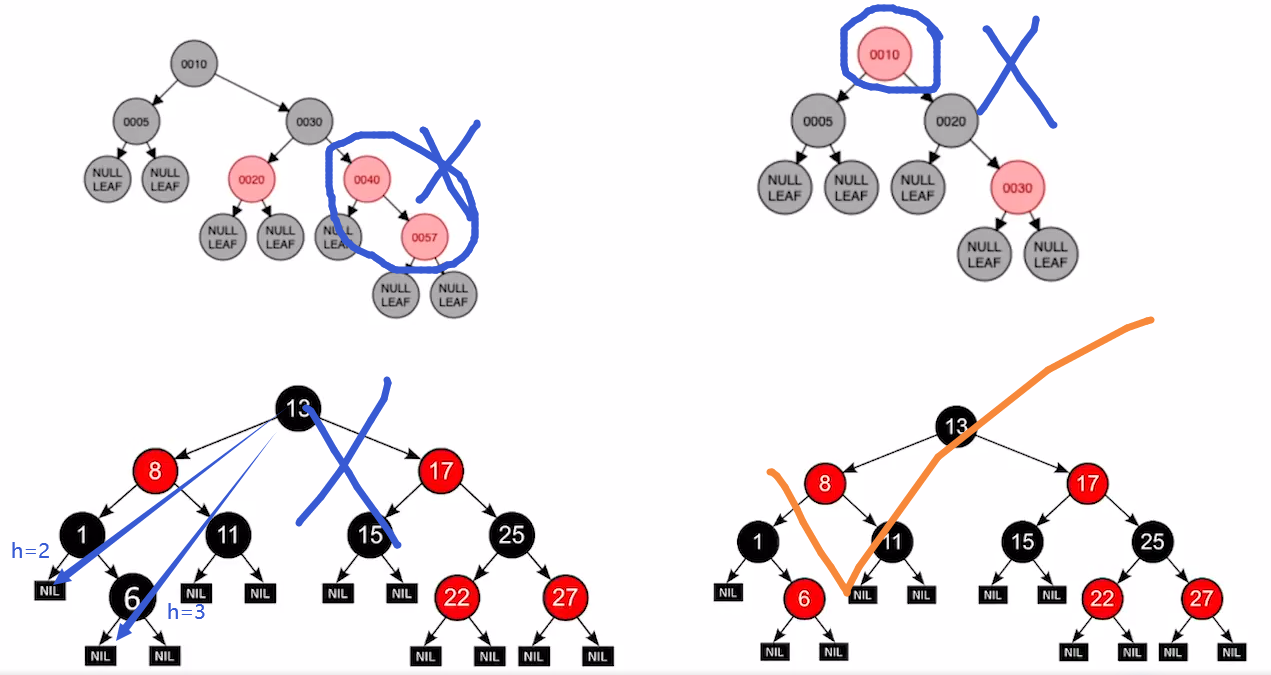
　　了解定义之后，黑高：由于“黑路同”，所以到达任意叶结点的黑节点个数就是黑高。

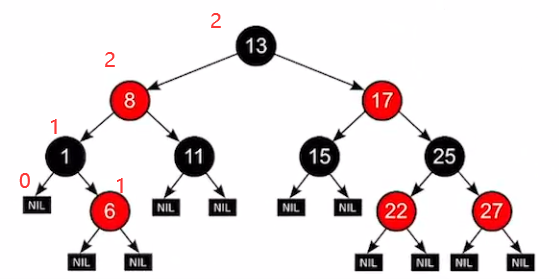
两个性质

1. 根节点到叶结点的最长路径不大于最短路径的二倍
2. 有n个内部节点(是内部结点，不包括null的哦)的红黑树高度 h < log2(n+1)

 

补充

1. 时间复杂度O(log2n)
2. 那如果黑高为h，内部节点至少为2^n-1，既这种全满的情况

 

 

　　下面重点来了，就是红黑树的插入，本来只想模拟一遍这个，闲手动太麻烦才第一次写博客，那么下面就详细模拟红黑树的插入过程

　　首先来回顾平衡二叉树的插入

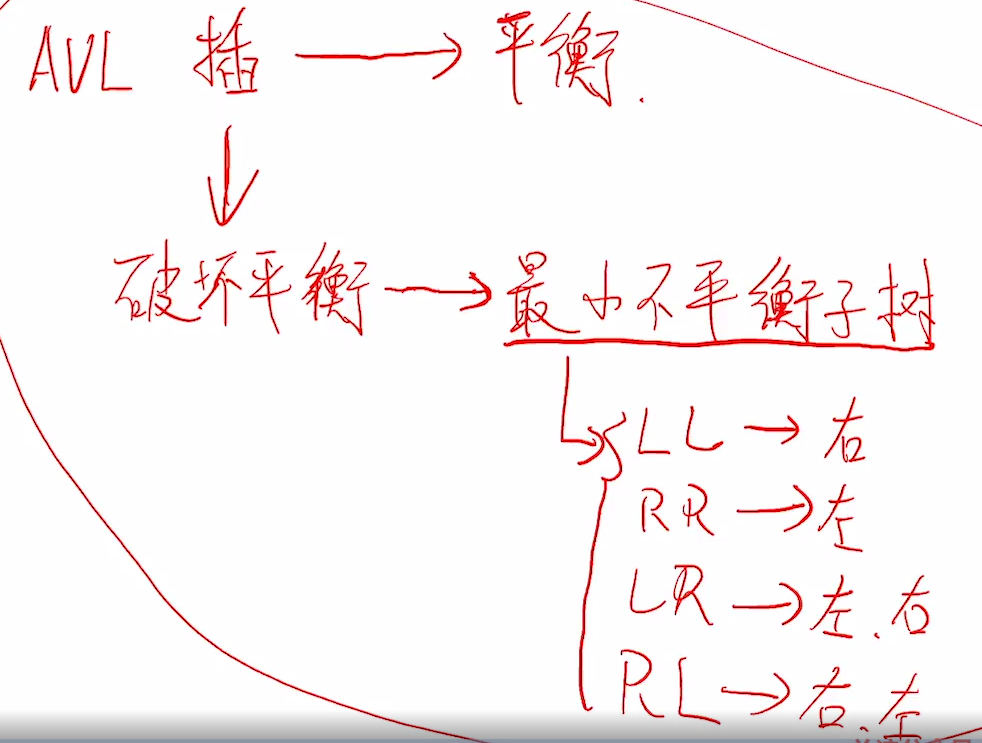
　　其实红黑树就是先通过普通排序树的插入，对于叔叔节点的颜色，选择变换方式，

　　跟魔方一样，记住口径自然而成，（其实不计口诀也行）

 

　　 模拟完这一个，就一点问题没有了，对于每次插入，都对比这个方法，自然就会解决

　　下面开始对于每个节点的插入开始分部模拟

 1.

2.

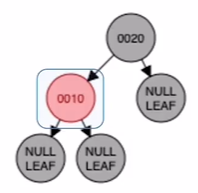
3.爷爷的左边是父亲，父亲的左边是他，所以是ll

4.

5.

6.

7.

8.

9.

10.

11.

12.

 

13.先是LR的，让儿子到爷爷的位置，然后儿爷染色

 

 

 14、看叔叔，变完是LR，所以先左旋后右旋，让儿子到爷爷的位置，然后儿爷染色

15.

16.这个节点已经有了，不用插入，这样就完成了全部的红黑树插入

 

 

　　其实，这样看下来可能没有这么清晰，我第一遍听完感觉一般，但是这样一步步模拟下来，感觉已经醍醐灌顶，强化之前估计忘不掉了，感觉还是很有用的，而且平衡二叉树也更加贯彻了

　　写笔记总共耗时一小时多一丢丢，反正累了写写就当休息了，收获很多，希望看到这个都有帮助。

　　如果不清楚，建议去看王道原视频，我觉得讲的很清晰。ok了，结束。2023-05-16