贪心算法 --- 例题3.单源最短路径问题

一.问题描述

有向图G的每条边都有一个非负的长度c [i][j]，路径的长度即为此路径所经过的边的长度之和。
给定一个源点,求出从源点出发,到该有向图中其它各顶点的最短路径.

二.解题思路

Dijkstra算法是解决单源最短路径问题的贪心算法。其基本思想是:

一个例题:

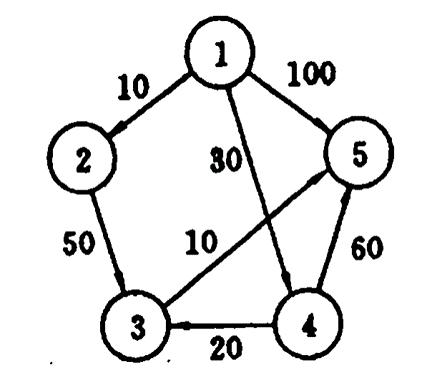
表格中默认选取的起始顶点为1顶点，所以本问题就转化为求解1顶点到2, 3, 4, 5这几个顶点的最短路径。首先初始条件列出1顶点到2, 3, 4, 5各个顶点的距离，这个距离直接在图的存储邻接矩阵中得到，选取距离最近的一个也就是2顶点加入集合S，下面要进行的是比较关键的一步，这个时候应该去获取3, 4, 5三个顶点到集合S的最短距离(从1顶点出发，可以经过S中的任意顶点)：将1到2顶点的距离加上2到各个点的距离，然后用这个距离来同1到各个顶点的距离相比较，谁小就取谁，以此类推，然后每次取Distance[]最小的值进入集合S。

这样下去，Distance[]中存放的就是每个顶点到集合S的最短距离.由于每一次的比较都是在上一次集合的最优结果中计算的，所以新计算出来的顶点Vi到集合S的最短距离也是全局最优的。

代码如下:

//求解单源最短路径的Dijkstra贪心算法
void Dijkstra(int n, int v, Type dist[], int prev[], int c[][N])  //单源最短路径的贪心算法Dijkstra
{
    bool s[n+1] = {false};
    for(int i=1; i<=n; i++)  //初始化
    {
        dist[i] = c[v][i];
        s[i] = false;
        if(dist[i] == inf) prev[i] = 0;
        else prev[i] = v;
    }
    dist[v] = 0, s[v] = true, prev[v] = -1;
    for(int i=1; i<=n; i++)
    {
        int temp = inf;
        int u = -1;
        for(int j=1; j<=n; j++)  //每一次从V-S集合中找出dist[j]最小的,加入S集合
        {
            if(!s[j] && dist[j]<temp)
            {
                u = j;
                temp = dist[j];
            }
        }
        if(u == -1) break;  //V-S集合中已经没有与S集合中任意点相连的点,退出
        s[u] = true;
        for(int j=1; j<=n; j++)   //更新dist数组
        {
            cout<<"Flag1: "<<i<<" j:"<<j<<endl;
            cout<<"s[j]: "<<s[j]<<"  c[u][j]: "<<c[u][j]<<endl;
            if(!s[j] && c[u][j]<inf)
            {
                int newdist = dist[u] + c[u][j];
                if(newdist < dist[j])
                {
                    dist[j] = newdist;
                    prev[j] = u;
                } 
            }
        }
    }
}

参考毕方明老师《算法设计与分析》课件.

欢迎大家访问个人博客网站---乔治的编程小屋,和我一起努力!