201800624模拟赛T2——回家路上

题目描述

很多学生都抱怨浪费在回家路上的时间太长。这天dongdong刚走出学校大门，就听说某段路在施工(但不知道是哪条路)，有可能导致他回家的时间会变长。

Dongdong给出了一张地图，图中标号为1的点是学校，标号为N的点是他家，以及一些点之间的路和走完每条路需要的时间。现在dongdong做了最坏打算，他想知道在最坏情况下，他回家的最短时间是多少。

输入格式

第一行两个数N和M，表示点的个数，边的个数。（这是无向图）

接下来M行，每行三个数A，B和V，表示点A和点B之间有一条需要走V分钟的路。

输出格式

一行，表示最坏情况下回家需要花费最少的时间。

输入样例

5 7
1 2 8
1 4 10
2 3 9
2 4 10
2 5 1
3 4 7
3 5 10

输出样例

27

数据规模

对于70% 的数据 \(N\le 100\)；

对于100% 的数据 \(N \le 1000, M \le \frac{n^{2}-n}{2}, 1\le A\le B \le N, 1 \le V \le 1000\)。

题解

这题暴力分挺多的，有70分。先求出\(1\to N\)的最短路，然后大力删除最短路上的每一条边，每删一遍都跑一遍最短路，统计一下即可。

值得一提的是，由于本题是稠密图，所以用不加任何优化的dijkstra算法比较好，（总复杂度\(O(n^3)\)，因为最短路径上的边数最多只可能有\(n-1\)条），比对优化的少一只\(\log\)。

下面讲一下正解：

对于这张图，我们先以1为源点跑一遍dijkstra，记录下路径，在以N为起点跑一遍最短路。

对于任意一个结点\(T\)，其最短路一定是这样的：

\(P\)可能与\(1\)点重合。

我们把每个结点的的\(P\)记录下来，我们暂且把它记为\(P_{1}, P_{2}, \cdots, P_{N}\)，这我们可以用类似并查集的数据结构维护，也可以预处理出来：

/**
 * ddd是P数组
 * fa[x]是在1->x的最短路中x的上一个结点是什么
 **/

inline int getfa(int x)
{
	return ddd[x] ? ddd[x] : ddd[x] = getfa(fa[x]);
}

inline void getl(int from, int to)
{
	ljc = 1;
	ddd[from] = 1;
	for(int i = to; i != from; i = fa[i])
		ddd[i] = ljc++;
	for(int i = to; i != from; i = fa[i])
	{
		ddd[i] = ljc - ddd[i] + 1;
		mmap[i][fa[i]] = mmap[fa[i]][i] = inf;//把最短路上的边大力删除，下面会说 
	}
	for(int i = 1; i <= n; ++i)
		ddd[i] = getfa(i);
}

那么对于一条边\(f\to t\)（假设\(f\to t\)不是\(1\to t\)最短路或\(f\to N\)最短路中的一条，因为如果是我们可以忽略不计，应为这样结果是相同的），什么情况下\(1\to N\)的最短路径可能经过改变呢？

答案是当\([P_{f}, P_{t}]\)中的有一条路径被切断时。

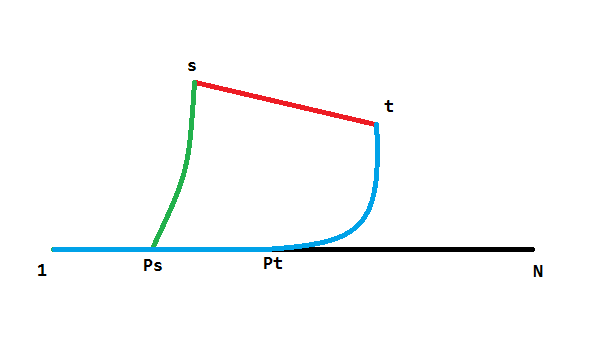
如图，如果\(1\to P_{s}\)中的一条被切断了，那显然\(s\to N\)的最短路比\(s\to t \to N\)不劣；如果\(P_{t}\to N\)中的一条被切断了，那显然\(1\to t\)的最短路比\(1\to s \to t\)不劣。

于是，我们可以用线段树维护\(1\to N\)最短路的边如果删去最终的最短路，枚举所有除\(1\to N\)最短路边外的所有边，对于每个\(s\to t\)，都把\([P_{s}, P_{t}]\)的区间与\(1\to s \to t\)取\(\min\)，最终答案为所有边删去所得的最短路的最大值。

代码细节还是挺多的，调了好久（好吧可能是我太菜了）……

#include <cstdio>
#include <cctype>
#include <cstring>
#include <algorithm>

using namespace std;

#define fill(a) memset(a, 0x3f, sizeof(a))
#define clr(a) memset(a, 0, sizeof(a))

#define dd c = getchar()
inline void read(int& x)
{
	x = 0;
	int dd;
	for(; !isdigit(c); dd);
	for(; isdigit(c); dd)
		x = (x<<1) + (x<<3) + (c^48);
	return;
}
#undef dd

#define maxn 1050
#define inf 0x3f3f3f3f

int mmap[maxn][maxn];//反正都是n2，就偷懒用了邻接表
int n, m;
int ljc;

struct DIJKSTRA//其实从N开始的dijkstra只要求最短路就可以了，但还是偷懒打了结构体
{
	int dist[maxn];//最短路
	int ddd[maxn];//刚才说的P数组
	int fa[maxn];//fa[x]是在from->x的最短路中x的上一个结点是什么
	bool vis[maxn];

	inline void dijkstra(int from)//由于是稠密图，用不加优化的dijkstra更快
	{
		fill(dist);
		clr(vis);
		dist[from] = 0;
		int noww;
		for(int kk = 1; kk <= n; ++kk)
		{
			noww = 0;
			for(int i = 1; i <= n; ++i)
				if(!vis[i] && (!noww || dist[noww] > dist[i]))
					noww = i;
			vis[noww] = true;
			for(int i = 1; i <= n; ++i)
				if(!vis[i] && mmap[noww][i] + dist[noww] < dist[i])
				{
					dist[i] = mmap[noww][i] + dist[noww];
					fa[i] = noww;
				}
		}
	}

	inline int getfa(int x)
	{
		return ddd[x] ? ddd[x] : ddd[x] = getfa(fa[x]);
	}

	inline void getl(int from, int to)
	{
		ljc = 1;
		ddd[from] = 1;
		for(int i = to; i != from; i = fa[i])
			ddd[i] = ljc++;
		for(int i = to; i != from; i = fa[i])
		{
			ddd[i] = ljc - ddd[i] + 1;
			mmap[i][fa[i]] = mmap[fa[i]][i] = inf;//把最短路上的边大力删除
		}
		for(int i = 1; i <= n; ++i)
			ddd[i] = getfa(i);
	}
} fs, ft;

#define ls(x) (x<<1)
#define rs(x) (x<<1|1)

struct Tree
{
	int node[maxn];

	inline void build()
	{
		fill(node);//并不用建树，直接全赋最大值即可
	}

	inline void update(int l, int r, int k, int L, int R, int tt)
	{
		if(L <= l && r <= R)
		{
			node[k] = min(node[k], tt);
			return;
		}
		int mid = (l+r) >> 1;
		if(mid >= L)
			update(l, mid, ls(k), L, R, tt);
		if(mid < R)
			update(mid+1, r, rs(k), L, R, tt);
	}

	inline int query(int l, int r, int k, int pla)
	{
		if(l == r)
			return node[k];
		int mid = (l+r) >> 1;
		if(pla <= mid)
			return min(node[k], query(l, mid, ls(k), pla));
		else
			return min(node[k], query(mid+1, r, rs(k), pla));
	}
} tr;

int main()
{
	freopen("road.in", "r", stdin);
	freopen("road.out", "w", stdout);
	read(n);
	read(m);
	fill(mmap);
	for(int i = 1, f, t, d; i <= m; ++i)
	{
		read(f), read(t), read(d);
		mmap[f][t] = mmap[t][f] = d;
	}
	fs.dijkstra(1);
	ft.dijkstra(n);
	fs.getl(1, n);
	tr.build();
#define m (min(fs.dist[i] + ft.dist[j], ft.dist[i] + fs.dist[j]) + mmap[i][j])
#define l min(fs.ddd[i], fs.ddd[j]) + 1
#define r max(fs.ddd[i], fs.ddd[j])
	for(int i = 1; i <= n; ++i)
		for(int j = i + 1; j <= n; ++j)
			if(mmap[i][j] < inf)
				tr.update(1, ljc, 1, l, r, m);
#undef m
#undef l
#undef r
	int ans = 0;
	for(int i = 2; i <= ljc; ++i)
		ans = max(ans, tr.query(1, ljc, 1, i));
	printf("%d", ans);
	fclose(stdin);
	fclose(stdout);
	return 0;
}