数据校验 奇偶校验，海明码校验，CRC校验

数据校验：

校验数据完整性的一种操作。 对原始数据使用一种算法计算出一个校验值，接收方使用相同的想法计算一个校验值。若两个校验值相同，则数据传输完整。

码字：

若干代码组成的字

码距：

将两个码字进行对比，不同的位的个数称为距离，对于一种编码方案，各码字之间距离最小的成为码距。

当码距d =1 时，没有检错能力。

比如00 出错变为01 仍然是合法的编码，无法发现错误。

 

 

 而d = 2时，有冗余的编码状态，若出错时变换成非法状态则可以检查到错误。

 

 

 

结论是：

 

 

 从信息论的角度看， d =2 可以表示两种信息，即 true or false， d >3 时可以表示是否出错，以及出错的位置。

 

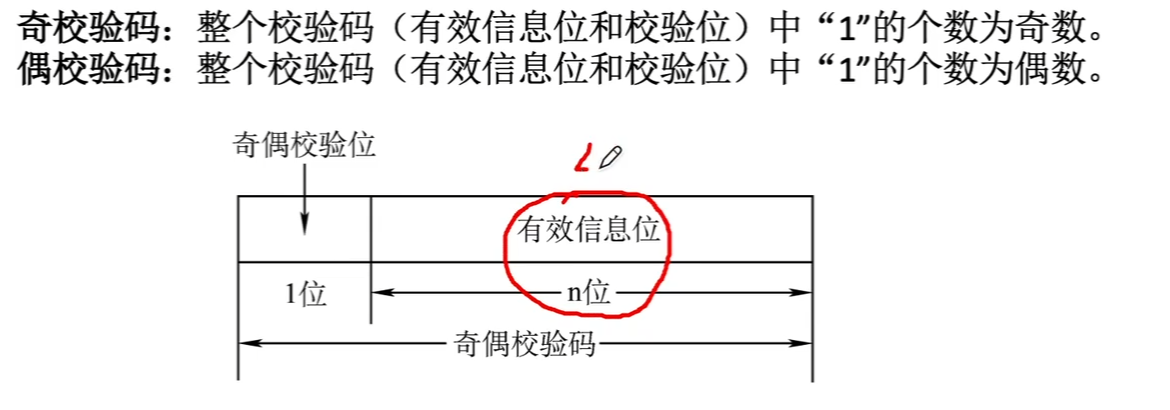
奇偶校验：

对有效信息位添加一位奇偶校验位。以奇校验码为例，添加的这位校验码保证整个编码中1的个数为奇数。

偶校验码则是保证添加后1的个数为偶数。

 

 

 如何计算1的个数？

异或。 （不进位相加）

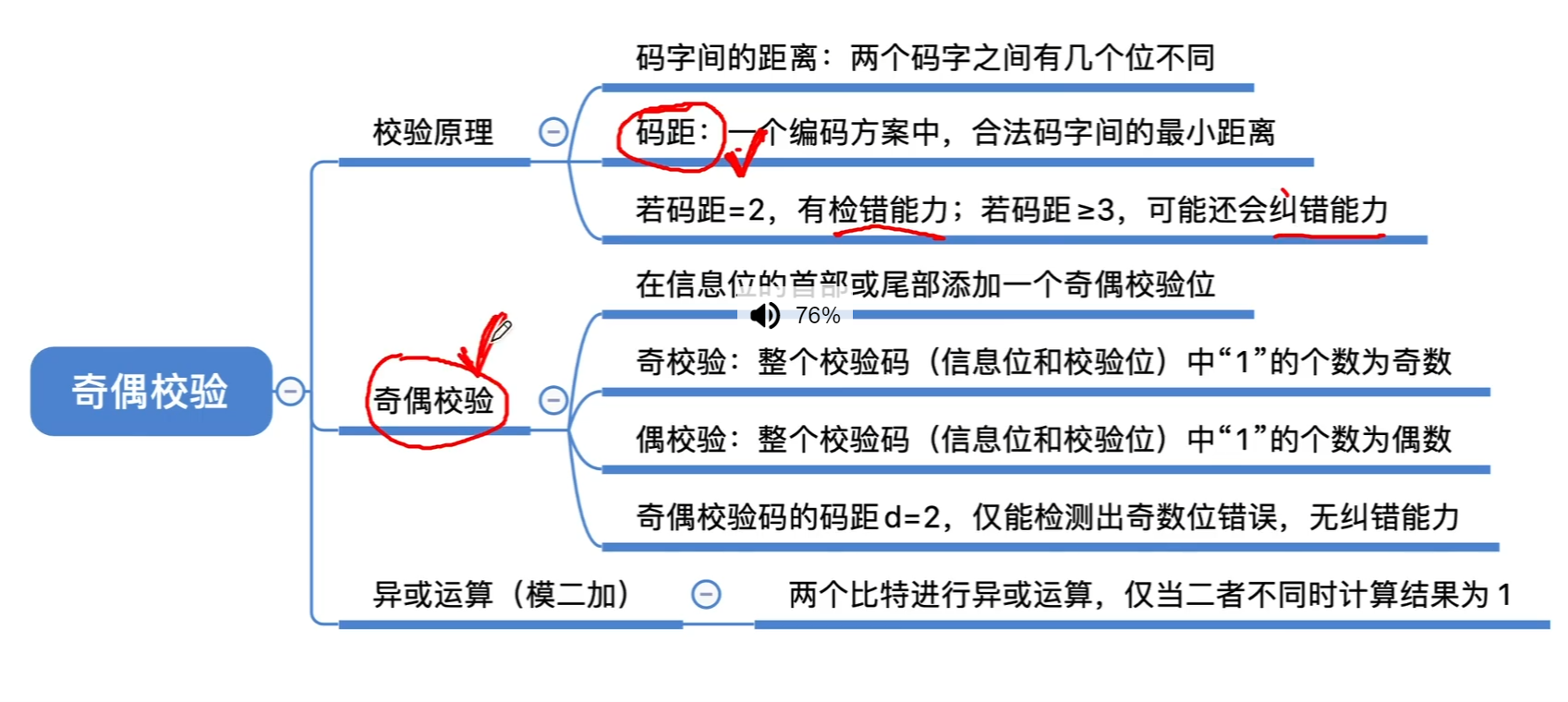
奇偶校验的性质：

码距d = 2 ，只能发现奇数位错误。无法纠错。

 

 

 

 海明校验码：

奇偶校验码添加一位校验位，只能表示两种状态， true or false。

而海明码将信息位分组进行偶校验。有多个校验位，就能够表示多种状态。

信息位：n

校验位：k

一共有 n + k 位数据。 即n+k 个可能出错的位置。

而 校验位能表达的信息有 2^n 种。

只需要 2^k > n + k + 1 (出错状态 + 1 正确状态）

n和k的对应关系：

 

 

 

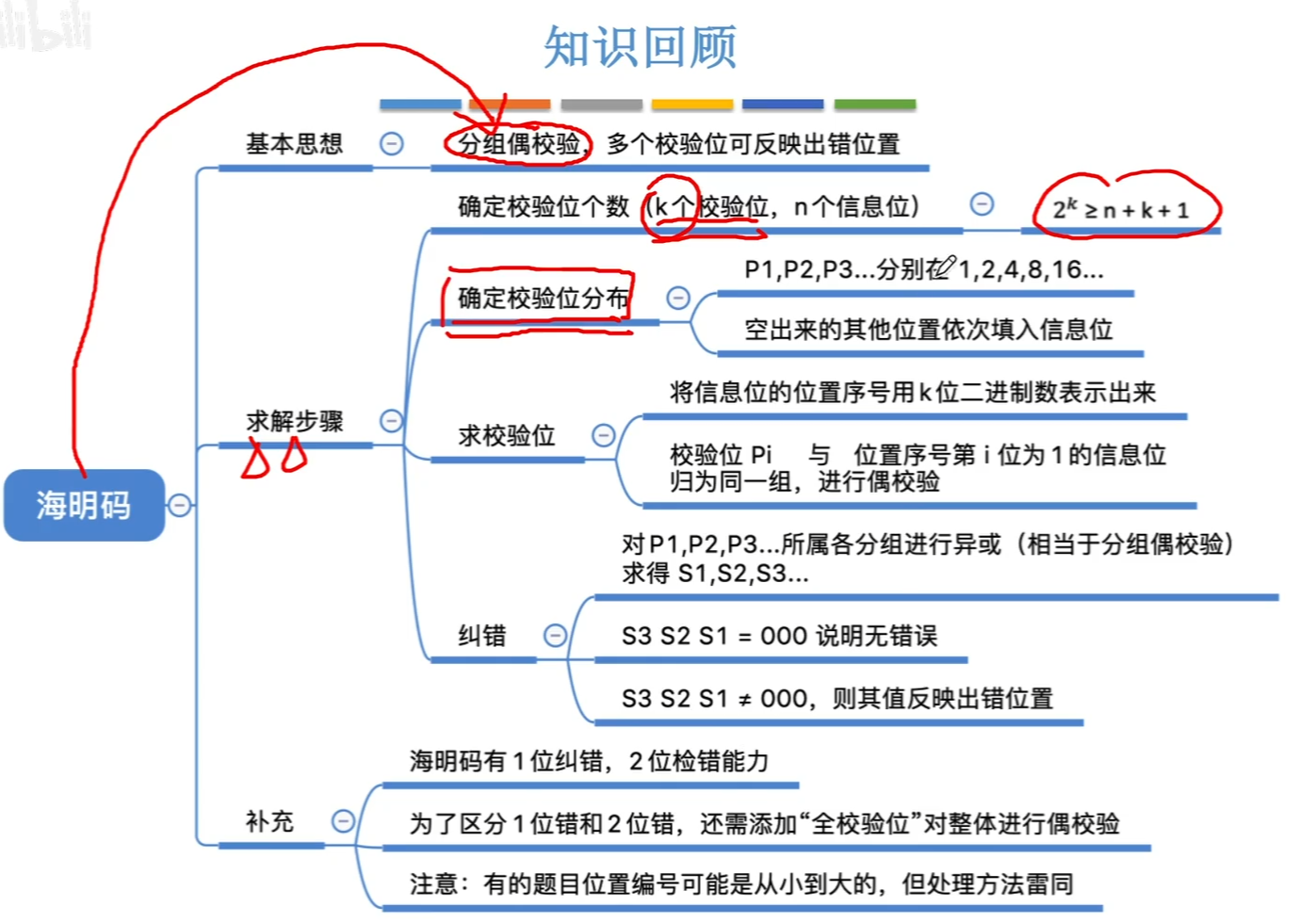
海明码求解步骤（！！）：

1. 确定符号

以 n = 4 为例，即 有四个信息位。信息位：1010.  可以算出 k =3

则有 D4D3D2D1 （1010） 

校验码P3P2P1，3位。

对应的海明码为 H7H6H5H4H3H2H1 共 7位。

2. 确定校验码分布（！）：

校验码pi放在2^(i-1)的位置上。信息位按顺序放在其余位置。

可以将校验码看成i的权重。

p1 : 1 位置， p2： 2 位置....

 

 

 

3. 求解校验位的值：pi 

H3, H5, H6, H7为信息位。分别用3位2进制表示为：（用3位的原因是三个分组）

 

 

 完整的分布为：

 

 

 

4. 纠错

校验方程：

 

 

 如果接收方接收到：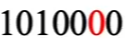

 

 

 第二位H2 即 p2 出错。

S3S2S1 = 010 表示第010（=2）出错。

直观解释：

s1 s2 s3是三个分组，三者之间有交叉和不同的地方。不同的错误与不同的区域一一对应。

 

 

 

缺点：

当两个bit 出现错误时，s3s2s1同样不为0，这时候海明码无法判断是1位错还是两位错。

而且海明码只能纠正1位的错误。

改进：

 

 

 总结：

 

 循环冗余校验码：

基本思想：

数据发送时约定一个除数，可以计算出一个余数。（数据 / 除数 = 余数），判断传输后余数是否改变。

 计算方式：

给定一个生成多项式，一个K bit信息码，我们需要计算它的R bit校验码，组成CRC码。

 

这个多项式对应二进制：1101 ，这个是约定好的除数。 使用3位校验位。 则一共 N = K + R = 9位。

1. 将信息位左移3位。低位补0

2. 对移位后的信息码用生成多项式对应的二进制码做模2 除法。产生3位余数为校验码。

模2除法： 做减法的时候实际上做异或预算。 比如第一个 1010 - 1101 = （0）111

 

 

求得：

 

 

检查与纠错：

接受到的校验码对之前确定的除数（生成多项式） 做模2除。

如果为0，无错。

如果不为0，则对应某位置出错。

余数与出错位置的对应。这种对应关系是由生成多项式确定的。

 

 

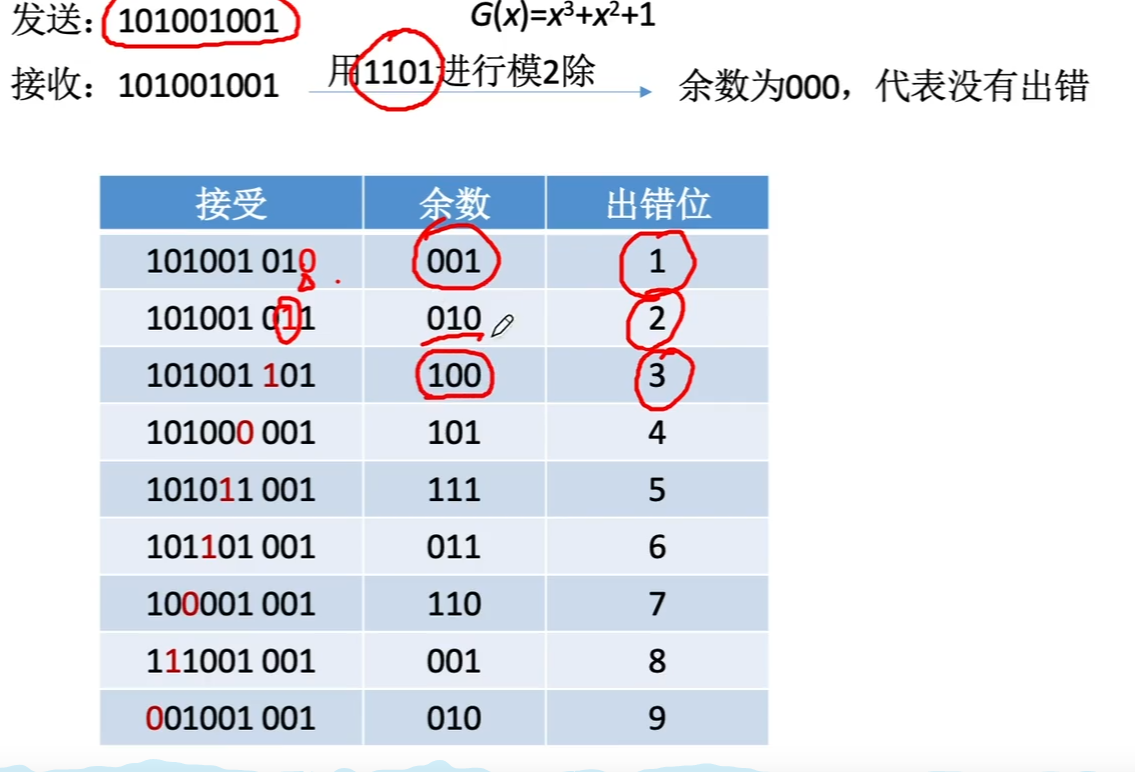
 可以看到其中对应关系有重复。

 

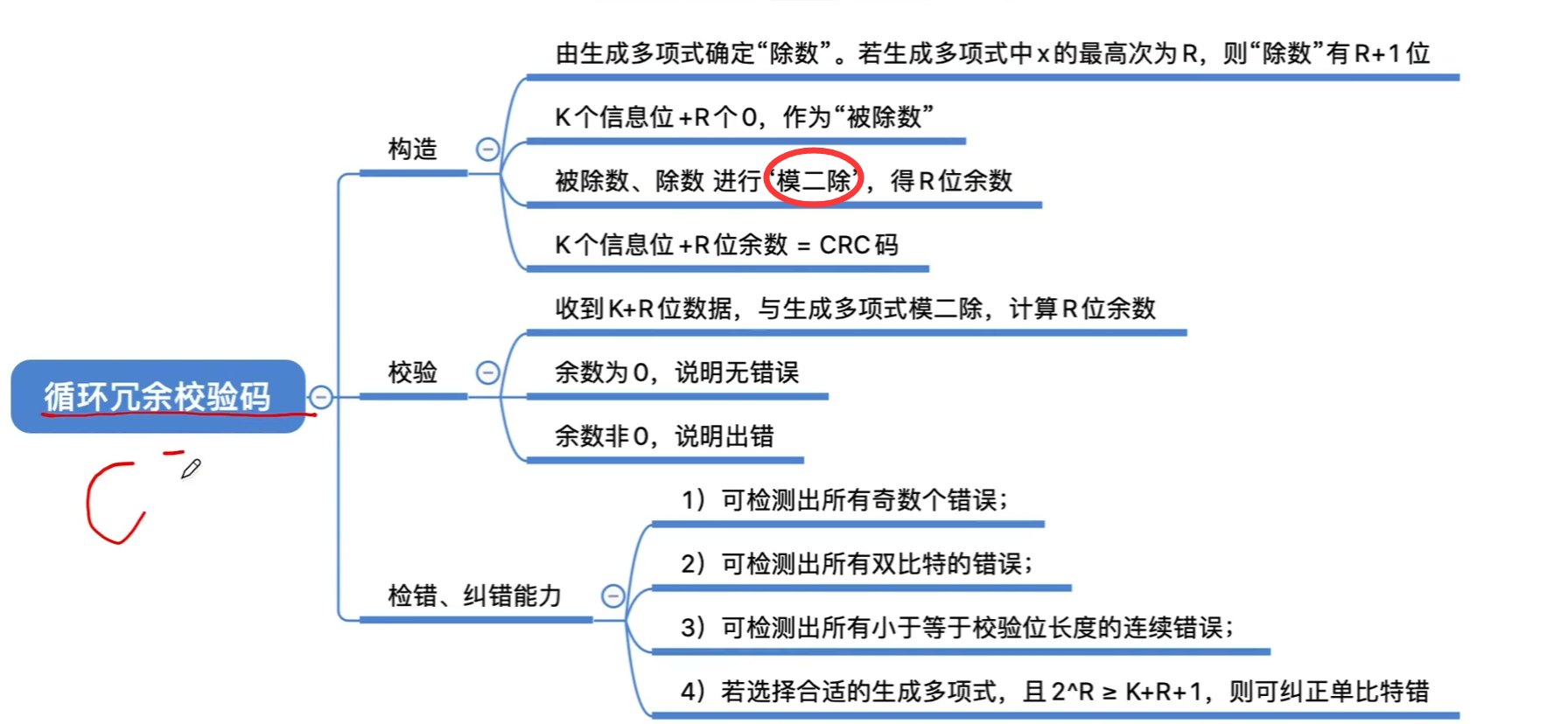
 总结：