秒懂 循环群 和 格
一、循环群
参考:https://zhuanlan.zhihu.com/p/68407532
在解释循环群之前,我默认你知道什么是代数系统,什么是半群,什么是群。
循环群的定义其实离不开循环两个字,想理解这两个字,不妨看一个例子。
我们看<Z6,+>中的元素{0,1,2,3,4,5}。取其中的元素1,不停地对自身进行模6加法,即对本身进行幂运算。
可得:
1^1=1
1^2=1+1=2
1^3=1+1+1=3
1^4=1+1+1+1=4
1^5=1+1+1+1+1=5
1^6=1+1+1+1+1+1=0(模6加法意义下)
1^7=1+1+1+1+1+1+1=1(模6加法意义下)
……
对1进行幂运算,就能得到该集合里的所有元素,然后不断循环。
我们称1为循环群<Z6,+>的生成元。
formal definition
若存在a∈G使得G=<a>,则称G是循环群,称a为G的生成元。
如果对其他元素不断求幂运算,我们可以得到:
元素0形成的结果只有0,可写成,结果集合为{0},
元素2、4形成的结果是一样的,结果集合为{0,2,4},
元素3形成的结果集合为{0,3},
元素1、5形成的结果为{0,1,2,3,4,5},
可以发现,1,5两个元素不断进行幂运算能够得到集合里的所有元素,我们称1,5位生成元。
并且,不同元素得到的结果相同,按照结果划分,并且称结果集合构成的群为子群。
关于做题:
有两个很重要的结论:
设循环群的阶数为n,循环群的一个生成元为a,小于等于n 且与n 互质的数依次为(x,y,z.....)
1. 小于等于n 且与n 互质的数的个数为生成元的个数,并且生成元为:a^x ,a^y, a^z ......
2. n的正因子个数数为子群个数,正因子数为子群长度
有一道很好的例题参考:https://blog.csdn.net/kindoms214/article/details/83051821?utm_medium=distribute.pc_relevant.none-task-blog-BlogCommendFromBaidu-1.control&depth_1-utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromBaidu-1.control
二、格
关于格,我确实是学不怎么明白,只能罗列几个概念,做题的结论。(毕竟小镇做题家最擅长这个)
格的定义:

分配格: 格中任意元素满足分配律

结论:有砖石格和五角格的 就不是分配格。
有界格:有最大的,全上界。有最下的,全下界。

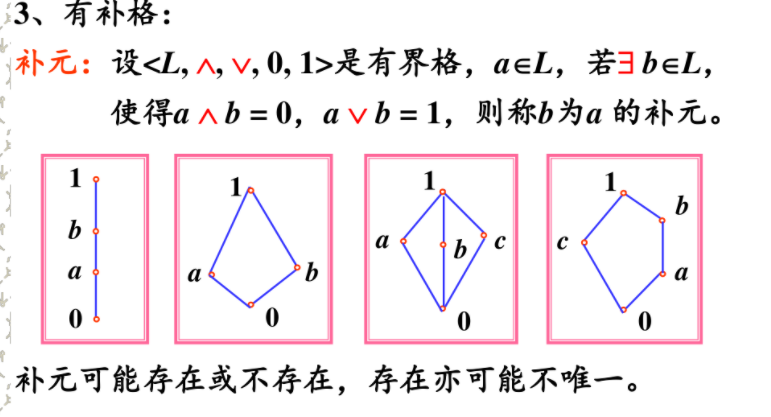
有补格:两个元素a,b求上界为1,求下界为0,则 b为a的补元。任取a 都有补元,则为有补格。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号