Hash Tables and Hash Functions

Reference: Compuer science

Introduction:

This computer science video describes the fundamental principles of the hash table data structure which allows for very fast insertion and retrieval of data. It covers commonly used hash algorithms for numeric and alphanumeric keys and summarises the objectives of a good hash function. Collision resolution is described, including open addressing techniques such as linear and quadratic probing, and closed addressing techniques such as chaining with a linked list.

 

 

 Consider a list:

 

 Find Ada

You can use linearly search, which costs the time of O(n)

Or you happend to know the index of ada(8), you can look up the value very quickly.

this costs you the time of O(1)

Can help wondering that what if we encode the name into index would the look-up process become O(1).?

Absolutely!

we can turn the key(i.e. the name) into a number(index) with a hash function.

Let's say take each letter of the word get its ascii code,add them up,divided by the length of the array,get the remainder.

 

 Namely , the hash function here is :

 

 we can serve the properties of a person as the value,the name as key.

So that we can look up the profile of a person by the key(i.e.name)

 

 Notes:

 

 So far you aquire the ability to transform a key into index, you can look up very information by hash table.

Needless to say, that is unrealistic.

 

 Have you ever consider the case that two different key are truned into a same index number?

That is collisions.

Let's look a example.

 

 

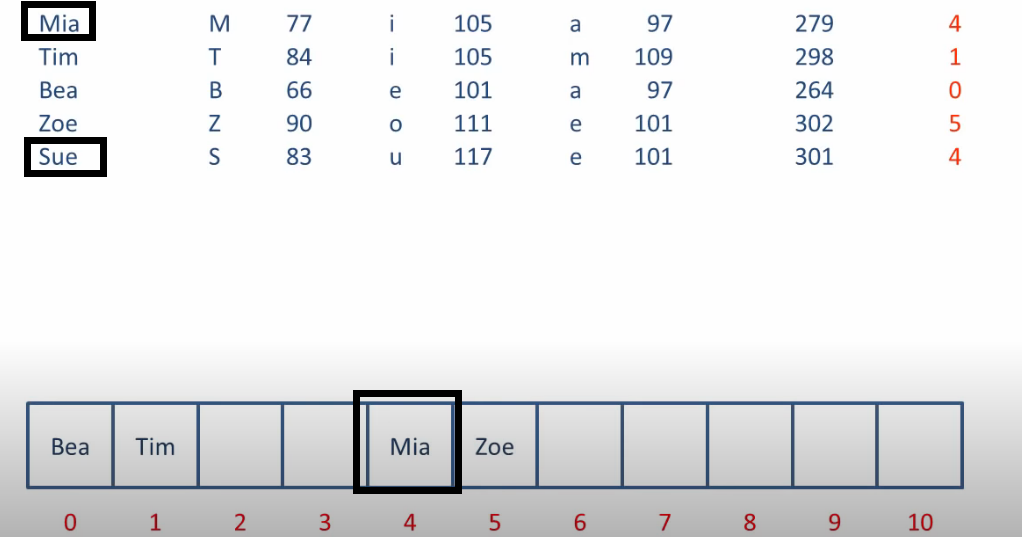
How to solve collisions?

we can put sue into  the next place index5 which is empty.

Basically we can put the one that causes collision into the next empty place.

this is linear probing.

put the element somewhere other than the caculated adress is call  open adressing.

because every location is open to every elements.

we can use a varity of techniques to decide where to palce. 

If we get to the end of the array still can't  find a empty place,

it may cycle around to the start of the array.

As you can image , the indexing process is also involved linear probing.(linear search)

In the worse case scenario, it takes O(n) to store and search a key.

Need to mention:

 

 

Another way  to deal with collisions is called chaining. (close addressing)

we add a linked list in the collision index.

 

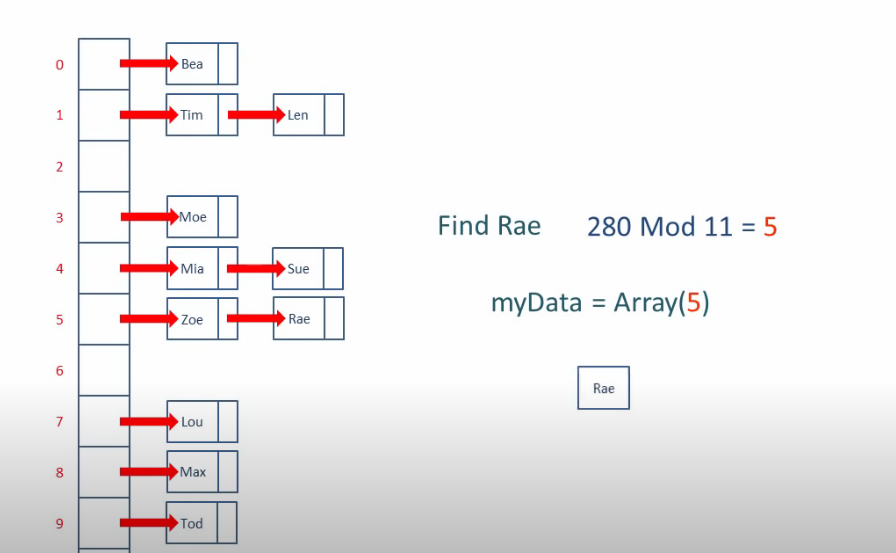
 traverse the linked list also takes time.

 

Summary: