汉诺塔问题(递归)

 

一.问题

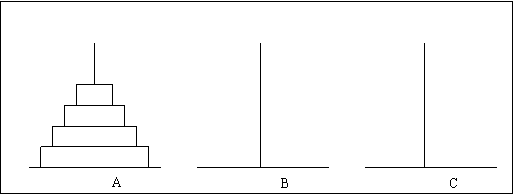
如下图所示，从左到右有A、B、C三根柱子，其中A柱子上面有从小叠到大的n个圆盘，现要求将A柱子上的圆盘移到C柱子上去，期间只有一个原则：一次只能移到一个盘子且大盘子不能在小盘子上面，求移动的步骤和移动的次数

 

 

二.算法思路

1. 将A柱子上的较大的n-1个盘子暂时移到B柱子上
2. A柱子只剩下最大的盘子，把它移到目标柱子C上
3. 最后再将B柱子上的n-1个盘子移到目标柱子C上

 

三.对递归过程的理解

　　将每层函数看作一个人,分别为其编号(也就是第几层函数)。

 

　　对于每个人来说，没有A，B，C柱，只存在from(要搬的盘子所在的柱子), temp(过渡柱),to(目标柱)。其是针对每个人来说的，是不断变化的。

　　对于n号人来说，他会接到上一个人(n+1)所下达的任务：要把from柱上的n个盘子，搬到to柱上面，完成后将工作重新交给（n+1）号人

　　n号人完成任务(偷懒)的方式如下：

　　1:把from柱上的n-1个盘子，交给n-1号人，让他把盘子搬到temp柱上等待

　　2:把from柱上剩下的最后一个盘子搬去to柱

　　3:把temp柱上的n-1个盘子，交给n-1号人，让他把盘子搬到to柱。

　　4:将工作重新交给（n+1）号人

　　

　　还需要事先通知最后一个人(递归出口):你是最后一个人，你不需要通知下一个人，把仅剩的一个盘子从from搬到to就够了。

　　

四.代码

#include<stdio.h>
#include<math.h>
void hanoi(int n,char from,char temp,char to)
{
    if(n==1)printf("%c -> %c \n", &from, &to);//事先通知最后一个人(递归出口):你是最后一个人，你不需要通知下一个人，把仅剩的一个盘子从from搬到to就够了。
    else
    {
        hanoi(n - 1, from, to, temp);//把from柱上的n-1个盘子，交给n-1号人，让他把盘子搬到temp柱上等待
        printf("%c -> %c \n", &from, &to);//把from柱上剩下的最后一个盘子搬去to柱
        hanoi(n - 1, temp, from, to);//把temp柱上的n-1个盘子，交给n-1号人，让他把盘子搬到to柱。
    }

}
int main()
{
    int n;
    scanf_s("%d", &n);
    hanoi(n, 'A', 'B', 'C');
    return 0;
}

 

五.对自己的告诫

不要试图跟踪递归的全程，要以递归的方式来思考递归

递归的关键，在于边界，以及每层函数之间的关系