SAM小记
首先,读本章的人,要有一个思想:对于子串,我们考虑若在它前方或后方加字符,它的性质会有什么改变,或者不变
将 \(SAM\) 前,先讲 \(endpos\)
定义:
对于一个子串,它在原串中可能出现在若干的位置。而一个子串 \(p\) 出现的这些位置的右端点标号组成的集合,我们称之为 \(endpos(p)\)
例:对于字符串 \(abcab\),它的字串 \(ab\) 的 \(endpos\) 为 \(endpos(ab)={2,5}\)
定义:
把所有拥有相同 \(endpos\) 的子串,归为一个等价类
性质:
\(1\),两个不同的子串如果它们的 \(endpos\) 相同,那么:一个子串是另一个字串的后缀
证明:
对于一个子串,考虑在它后面加减字符,容易发现它们的 \(endpos\) 绝对不相同(考虑 \(endpos\) 集合里面最小的数,如果加字符,这个最小的数就会加 \(1\),如果减,这个最小的数就会减 \(1\))
考虑在它前面加减字符,若 \(endpos\) 相同,则必然一个字串是另一个字串的后缀
\(2\),两个字串 \(t\) 和 \(p\) (\(len_t<len_p\)),要么\(endpos(p)∈endpos(t)\),要么\(endpos(t)∩endpos(p)=∅\)
证明:跟上面的证明方法大同小异,不多赘述
\(3\),\(endpos\) 等价类的数量为 \(O(n)\) 级别
证明:最大的 \(endpos\) 等价类为 \(1 \sim n\),即子串为空的情况,根据结论 \(2\),他肯定会分为两个及以上不相交的子集,最后分成集合 \(1,2,3....n\),合并上来,也就 \(2n-1\) 个,所以也就是 \(O(n)\) 级别
前置知识结束,考虑构建 \(SAM\)
我们不妨定义(请结合后面内容阅读):
\(SAM\) 中一个点表示一个 \(endpos\) 等价类,同时也是 \(parent tree\) 上的一个点(不知道的去oi-wiki)
\(SAM\) 中一个点的 \(len\) 表示这个等价类最长子串长度,同时也表示从 \(1\) 号节点到该节点的最长路
\(SAM\) 中点往后连的边 \(s_i\) 表示当前子串向后加一个字符 \(s_i\)
\(SAM\) 中点的 \(fa\) 边表示与当前点不同 \(endpos\) 的最长后缀的位置,同时也表示在当前点最短子串前面减一个字符可以得到不同的 \(endpos\) 等价类
下面附上代码:
void add(int c)
{
int p=last;
int now=last=++tot;
gs[tot]=1;
for(;p&&!dian[p].ch[c];p=dian[p].fa) dian[p].ch[c]=now;
if(!p) dian[now].fa=1;
else
{
int to=dian[p].ch[c];
if(dian[to].len==dian[p].len+1) dian[now].fa=to;
else
{
int nq=++tot;
dian[nq]=dian[to];
dian[nq].len=dian[p].len+1;
dian[to].fa=dian[now].fa=nq;
for(;p&&dian[p].ch[c]==to;p=dian[p].fa) dian[p].ch[c]=nq;
}
}
}
int main()
{
scanf("%s",s+1);
len=strlen(s+1);
for(int i=1;i<=len;i++) add(s[i]-'a');
}
再附上一个图:
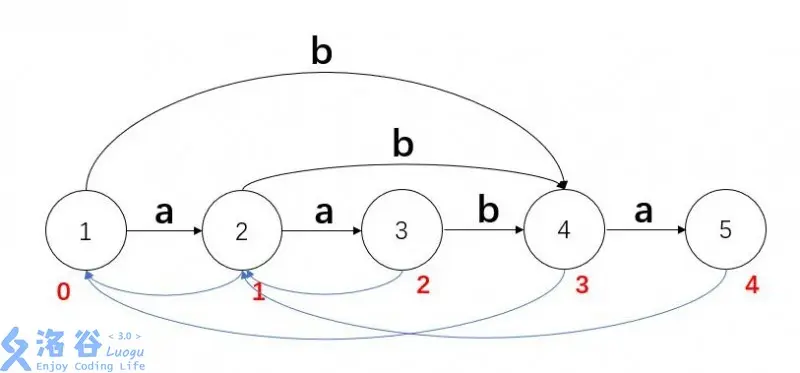
以 \(aabab\) 为例
首先,我们的 \(SAM\) 是动态开点:
对于新加入的点 \(s\),我们要完善他的信息,我们跳前面点的 \(fa\),看看所有的 \(fa\) 是否有连 \(s\) 的边,如果没有,那么连一条边到这个点
考虑跳到根节点都没有连 \(s\) 的边,则这个新节点,它的 \(fa\) 就是 \(1\) 号几点
如果有边,那么我们结合图来讲,假如我们加入的是 \(5\) 号节点,现在 \(1\) 有连向 \(2\) 的边,\(1\) 是 \(4\) 的 \(fa\),我们发现 \(len[1]+1==len[2]\)
什么意思呢,结合上面的定义,\(1\) 号节点中的子串往后加 \(a\) 可以得到 \(2\),\(4\) 号节点的子串往后加 \(a\) 可以得到 \(5\),\(4\) 号节点往前减字符可以的到 \(1\),那么就有 \(5\) 号节点往前减字符可以得到 \(2\)
再来一张图讲第三种情况:
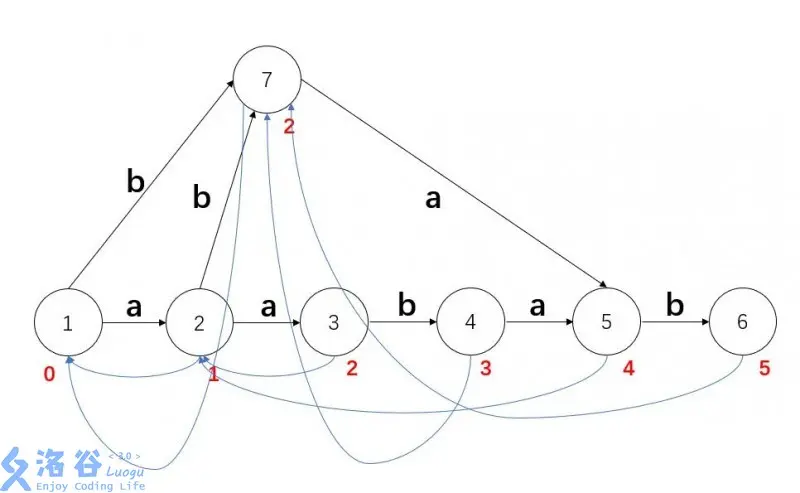
考虑我们现在加入了 \(6\) 号节点,我们发现 \(2\) 有连向 \(4\) 的边为 \(b\),什么意思呢?
就是 \(4\) 的 \(endpos\) 的等价类是 \(aab,ab,b\),但是 \(6\) 号节点是 \(aabab\),它的 \(fa\) 代表的等价类明显应该是 \(ab,b\),没有 \(aab\)
抽象一点讲,就是 \(4\) 节点所包含的集合太大,比 \(6\) 节点 \(fa\) 应该的集合还大
导致这个的原因是:\(2\) 到 \(4\) 节点不仅可以走一步,还可以走两步,导致第二种情况的证明在这种情况中不成立
因为没有节点可以当 \(6\) 节点的 \(fa\),但 \(6\) 节点的 \(fa\) 又是客观存在的,所以我们考虑新建节点 \(7\) 表示 \(6\) 的 \(fa\)。
此时 \(6\) 的节点信息已经完善完了,考虑完善 \(7\) 节点的信息
首先 \(7\) 必然是 \(4\) 的 \(fa\),因为 \(7\) 的 \(len\) 比 \(4\) 的 \(len\) 小,而 \(7\) 又是从 \(4\) 延伸出去的(即 \(7\) 和 \(4\) 的 \(endpos\) 原本一样,但是 \(7\) 的 \(endpos\) 因为 \(6\) 的加入多了一个 \(6\)),所以其 \(endpos\) 必然是 \(4\) 的超集,且是最小的超集
很明显一步可以到 \(4\) 节点的那些边应该更改为连向 \(7\) 节点,因为只有一步到可以满足 \(7\) 是 \(6\) 的 \(fa\) 的情况,而为了让它的信息不漏,应该所有一步到 \(4\) 的边都应该改向连 \(7\)。
\(4\) 可以到达的点 \(7\) 都可以到达,所以将 \(4\) 连向的信息都复制到 \(7\) 上。
这样 \(SAM\) 三种情况都讲完了。
用 \(SAM\) 上的点和边构建 \(parent tree\) 即可
最后,贴上例题正确代码。
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+50;
char s[N];
int len;
int last=1,tot=1;
struct jgt
{
int ch[26];
int len,fa;
}dian[2*N];
int gs[2*N];
void add(int c)
{
int p=last;
int now=last=++tot;
gs[tot]=1;
for(;p&&!dian[p].ch[c];p=dian[p].fa) dian[p].ch[c]=now;
if(!p) dian[now].fa=1;
else
{
int to=dian[p].ch[c];
if(dian[to].len==dian[p].len+1) dian[now].fa=to;
else
{
int nq=++tot;
dian[nq]=dian[to];
dian[nq].len=dian[p].len+1;
dian[to].fa=dian[now].fa=nq;
for(;p&&dian[p].ch[c]==to;p=dian[p].fa) dian[p].ch[c]=nq;
}
}
}
int h[2*N],e[2*N],ne[2*N],idx;
void jia(int a,int b)
{
e[idx]=b;
ne[idx]=h[a];
h[a]=idx++;
}
long long ans;
void dfs(int wz)
{
for(int i=h[wz];i!=-1;i=ne[i])
{
dfs(e[i]);
gs[wz]+=gs[e[i]];
}
if(gs[wz]!=1) ans=max(ans,1ll*gs[wz]*dian[wz].len);
}
int main()
{
memset(h,-1,sizeof h);
scanf("%s",s+1);
len=strlen(s+1);
for(int i=1;i<=len;i++) add(s[i]-'a');
for(int i=2;i<=tot;i++) jia(dian[i].fa,i);
dfs(1);
printf("%lld\n",ans);
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号