1.学习总结(2分)
1.1树结构思维导图
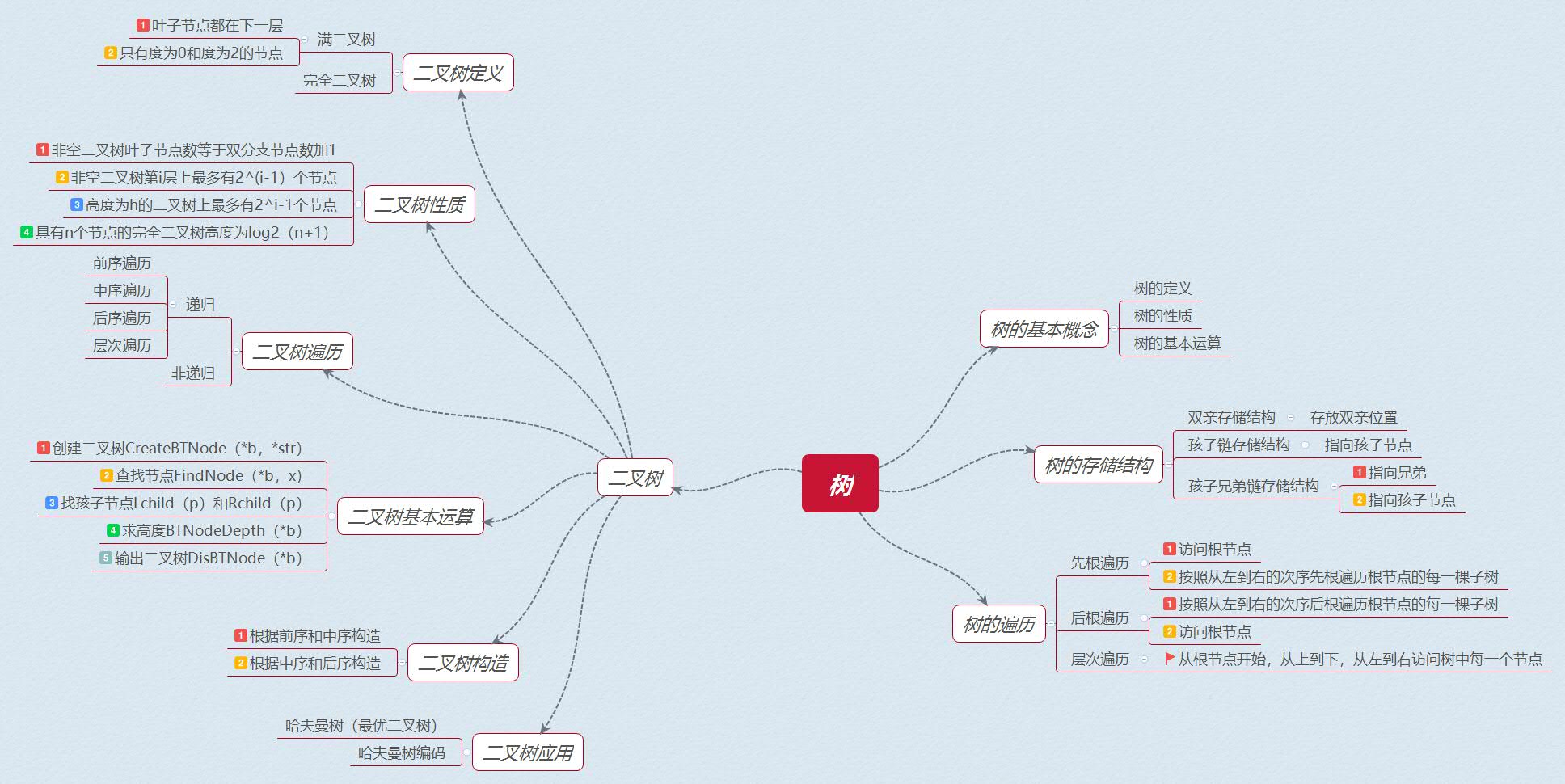
1.2 树结构学习体会
- 相当于栈和队列,树是比较难的。
- 还有很多知识点还没掌握,理解起原理来比较慢。
- 建树用递归快很多,之前用队列建树真是亏大了。
- 需要花时间去认真复习其中较难的知识点
2.PTA实验作业(4分)
题目1:6-4 jmu-ds-表达式树
1.设计思路
Q1栈存储数字
Q2栈存储运算符
while 字符串不为空
如果str[i]数字 创建树节点并进栈
否则 {
如果Q2栈顶元素优先级小于str[i] 运算符进栈
如果Q2栈顶元素优先级大于str[i] 创建新的根节点并赋予Q2栈顶元素,右左孩子分别取Q1栈顶元素后再次进Q1栈
否则 运算符出栈
}
计算表达式
如果为叶子节点
返回将字符转化为数字
X,Y分别存储树节点的左右子树
根据运算符进行相应运算
2.代码截图



3.PTA提交列表

题目2:7-1 还原二叉树
1.设计思路
输入先序遍历序列和中序遍历序列
调用函数BTNode *CreateBT1(char *pre,char*in,int n)
BTNode *CreateBT1(char *pre,char*in,int n):
创建二叉树节点b
利用循环找到中序序列中根节点的位置
定义k确定根节点在中序序列的具体位置
递归构造左子树=CreateBT1(pre+1,in,k)
递归构造右子树=CreateBT1(pre+k+-1,in+k+1,n-k-1)
对还原好的二叉树进行int length(BTNode *node)调用,计算二叉树高度
int length(BTNode *node):
如果node为空 则返回NULL
定义l计算左子树的高度l=length(node->left)
定义r计算右子树的高度r=length(node->right)
比较l和r的大小
l大则返回l+1
r大则返回r+1
2.代码截图
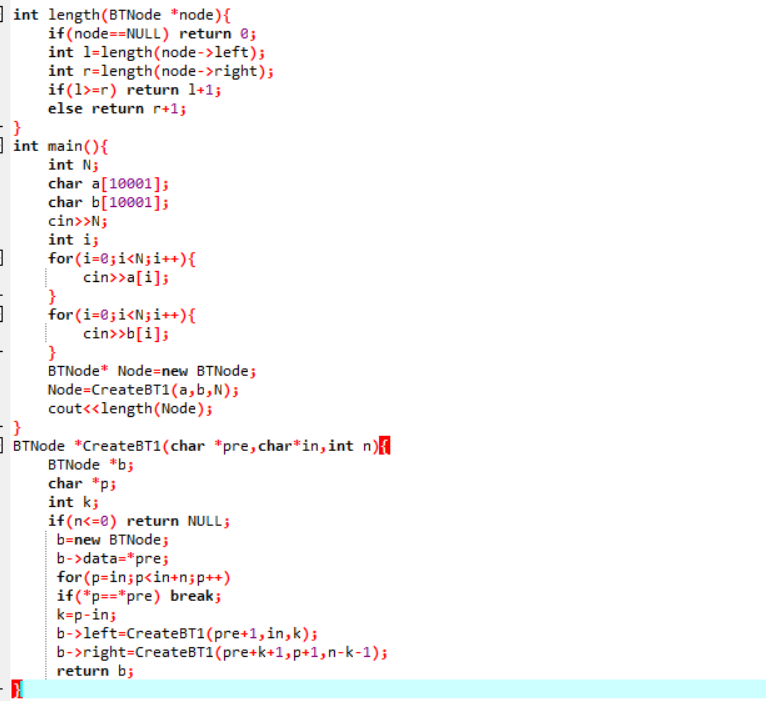
3.PTA提交列表

主要代码书上有,错了就翻书看下自己哪里错了.所以这题比较好做
题目3:7-1 还原二叉树
1.设计思路
输入中序和后序遍历
调用BTNode * Build(int n, int *mid, int *last)
BTNode * Build:
如果n为0,则返回NULL
创建二叉树节点rt
rt的data指向后序中的最后一个字符,即根节点
for i to n
在中序中找到根节点的位置,结束循环
创建rt的左子树= Build(i, mid, last)
创建rt的右子树=Build(n-i-1,mid+i+1,last+i)
返回rt
2.代码截图

3.PTA提交列表
刚开始一直是对部分,错误原因我也不懂,后面去网上找了下,发现把中序和后序的类型改为int形就对了,具体原因还不是怎么懂。
3.截图本周题目集的PTA最后排名
3.1 PTA排名
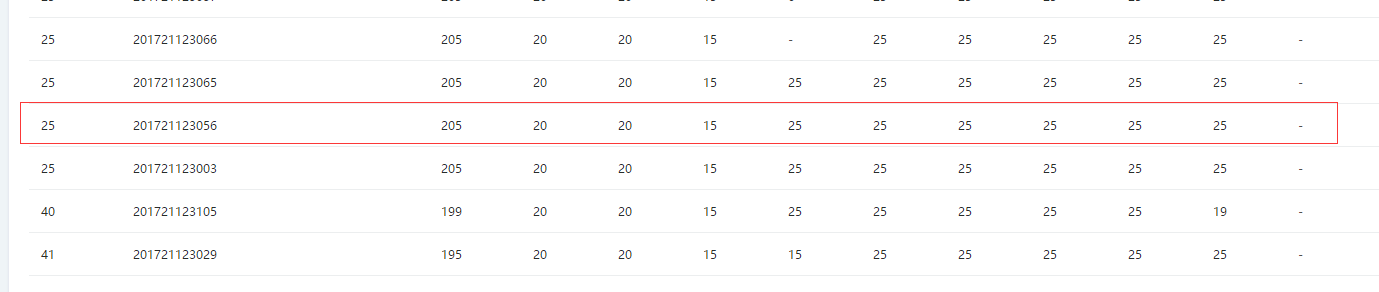
3.2 我的得分:
205:PTA总分在180--230分:2分
4. 阅读代码
#include <stdio.h>
#include <stdlib.h>
#define TRUE 1
#define FALSE 0
// 定义平衡二叉树的结点结构
typedef struct BiTNode
{
int data;
int bf; // 平衡因子
BiTNode *lchild, *rchild;
}BiTNode, *BiTree;
typedef int Status;
// 右旋处理,即LL调整
void R_Rotate( BiTree *p )
{
BiTree L;
L = (*p)->lchild;
(*p)->lchild = L->rchild;
L->rchild = *p;
*p = L;
}
// 左旋处理,即RR调整
void L_Rotate( BiTree *p )
{
BiTree R;
R = (*p)->rchild;
(*p)->rchild = R->lchild;
R->lchild = *p;
*p = R;
}
// 左平衡旋转处理,包括 LL 和 LR 调整
void LeftBalance( BiTree *T )
{
BiTree L, Lr;
L = (*T)->lchild;
switch( L->bf )
{
case 1: // 新结点插入在T的左孩子的左子树上,为LL型,作右旋处理即LL调整
(*T)->bf = L->bf = 0;
R_Rotate( T );
break;
case -1: // 新结点插入在T的左孩子的右子树上,为LR型,作双旋处理
Lr = L->rchild;
switch( Lr->bf )
{
case 1:
(*T)->bf = -1;
L->bf = 0;
break;
case 0:
(*T)->bf = L->bf = 0;
break;
case -1:
(*T)->bf = 0;
L->bf = 1;
break;
}
Lr->bf = 0;
L_Rotate( &(*T)->lchild ); // 先对T的左子树进行左旋处理即RR调整
R_Rotate( T ); // 再对T进行右旋处理即LL调整
}
}
// 右平衡旋转处理,包括 RR 和 RL 调整
void RightBalance( BiTree *T )
{
BiTree R, Rl;
R = (*T)->rchild;
switch( R->bf )
{
case -1: // 新结点插入在T的右孩子的右子树上,为RR型,作左旋处理即RR调整
(*T)->bf = R->bf = 0;
L_Rotate( T );
break;
case 1: // 新结点插入在T的右孩子的左子树上,为RL型,作双旋处理
Rl = R->lchild;
switch( Rl->bf )
{
case 1:
(*T)->bf = 0;
R->bf = -1;
break;
case 0:
(*T)->bf = R->bf = 0;
break;
case -1:
(*T)->bf = 1;
R->bf = 0;
break;
}
Rl->bf = 0;
R_Rotate( &(*T)->rchild ); // 先对T的左子树进行左旋即RR调整
L_Rotate( T ); // 再对T进行右旋即LL调整
}
}
// 若在平衡二叉树T中不存在和 e 具有相同数据的结点,则插入数据元素为 e 的新结点,
// 若因插入使二叉排序树失去平衡,则要作平衡调整,
// 布尔变量taller表示 T 的深度是否增加,TRUE表示增加,FALSE表示没有增加
Status InsertAVL( BiTree *T, int e, Status *taller )
{
if( !*T )
{
*T = (BiTree)malloc(sizeof(BiTNode));
(*T)->data = e;
(*T)->lchild = (*T)->rchild = NULL;
(*T)->bf = 0;
*taller = TRUE;
}
else
{
// 树中已有和e具有相同数据的结点,则不再插入
if( e == (*T)->data )
{
*taller = FALSE;
return FALSE;
}
if( e < (*T)->data ) // 继续在T的左子树进行搜索
{
if( !InsertAVL( &(*T)->lchild, e, taller ) ) // InsertAVL( &(*T)->lchild, e, taller )得到的是T的左孩子结点(*T)->lchild的 data,bf 等相关信息
{
return FALSE;
}
// 如果e已插入到T的左子树中,且左子树深度增加
if( *taller )
{
switch( (*T)->bf ) // 检查T的平衡因子
{
case 1: // 原本左子树比右子树高,再加上此结点,导致不平衡,需要作LL或LR调整
LeftBalance( T );
*taller = FALSE;
break;
case 0: // 原本左右子树等高,再加上此结点,左子树增高
(*T)->bf = 1;
*taller = TRUE;
break;
case -1: // 原本右子树比左子树高,再加上此结点,左右子树变为等高
(*T)->bf = 0;
*taller = FALSE;
break;
}
}
}
else // 在T的右子树进行搜索
{
if( !InsertAVL( &(*T)->rchlid, e, taller ) )
{
return FALSE;
}
if( *taller )
{
switch( (*T)->bf )
{
case 1: // 原先左子树比右子树高,现在左右子树等高
(*T)->bf = 0;
*taller = FALSE;
break;
case 0: // 原先左右子树等高,现在右子树增高
(*T)->bf = -1;
*taller = TRUE;
break;
case -1: // 原先右子树比左子树高,现在再加上此结点,导致不平衡,需要作 RR 或 RL 调整
RightBalance( T );
*taller = FALSE;
break;
}
}
}
}
return TRUE;
}
// 对于实例,我们可以这样创建平衡二叉树
void CreateAVL()
{
int i;
int a[10] = {2,1,0,3,4,5,6,9,8,7};
BiTree T = NULL;
Status taller;
for( i=0; i<10; i++ )
{
InsertAVL( &T, a[i], &taller );
}
}
- 分享一个创建平衡二叉树的代码。平衡二叉搜索树(Balanced Binary Tree)具有以下性质:它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。常用算法有红黑树、AVL、Treap、伸展树等。在平衡二叉搜索树中,我们可以看到,其高度一般都良好地维持在O(log(n)),大大降低了操作的时间复杂度。
- 给出代码相关地址https://www.cnblogs.com/zhangbaochong/p/5164994.html
5. 代码Git提交记录截图



 浙公网安备 33010602011771号
浙公网安备 33010602011771号