Lecture 4 -- LSTM

课件：Recurrent Neural Network (RNN) (ntu.edu.tw)

1. RNN

---

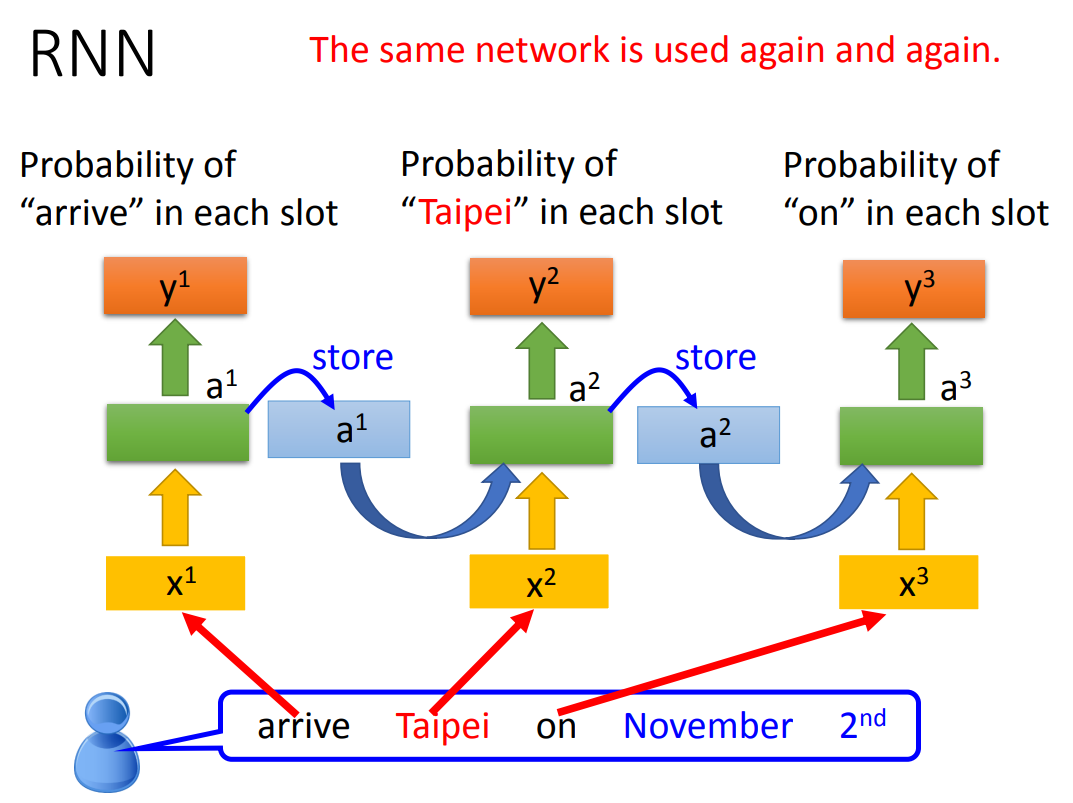
上图表示的RNN是三个模型吗？

不是！是一个模型被重复使用了三次！

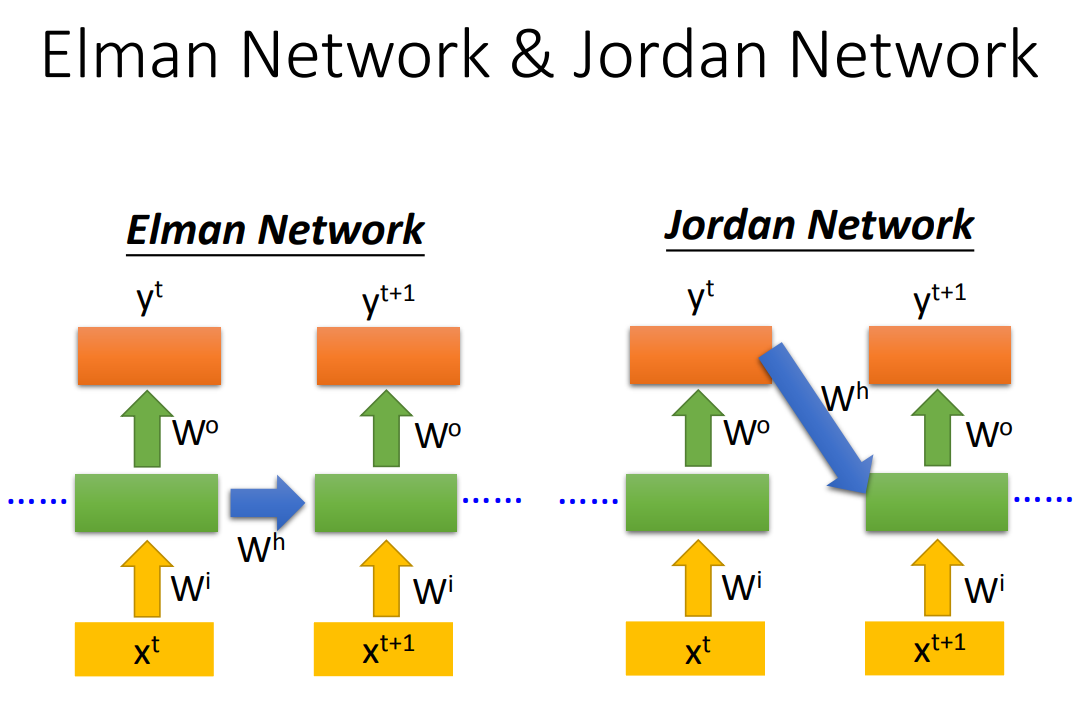
RNN分为两种：Elman Network和Jordan Network

Elman Network：Memory Cell储存的是隐藏层的输出

Jordan Network：Memory Cell储存的是模型的输出

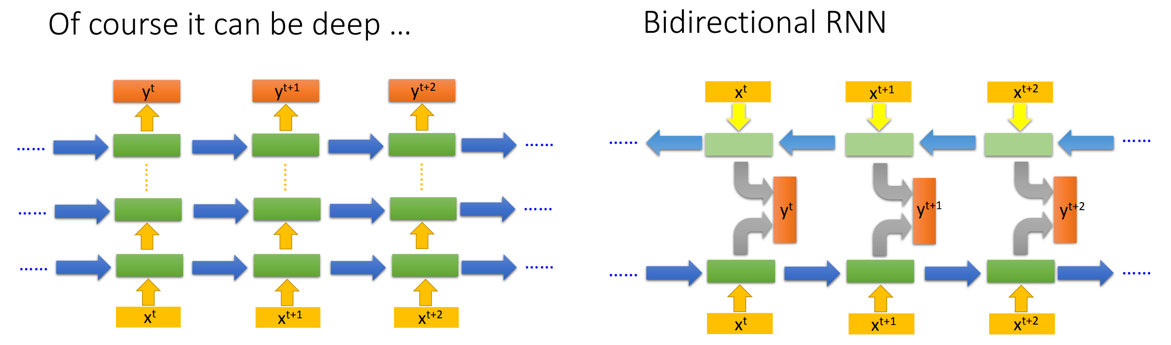
RNN可以是深层的，也可以是双向的！

 

 

2. LSTM

---

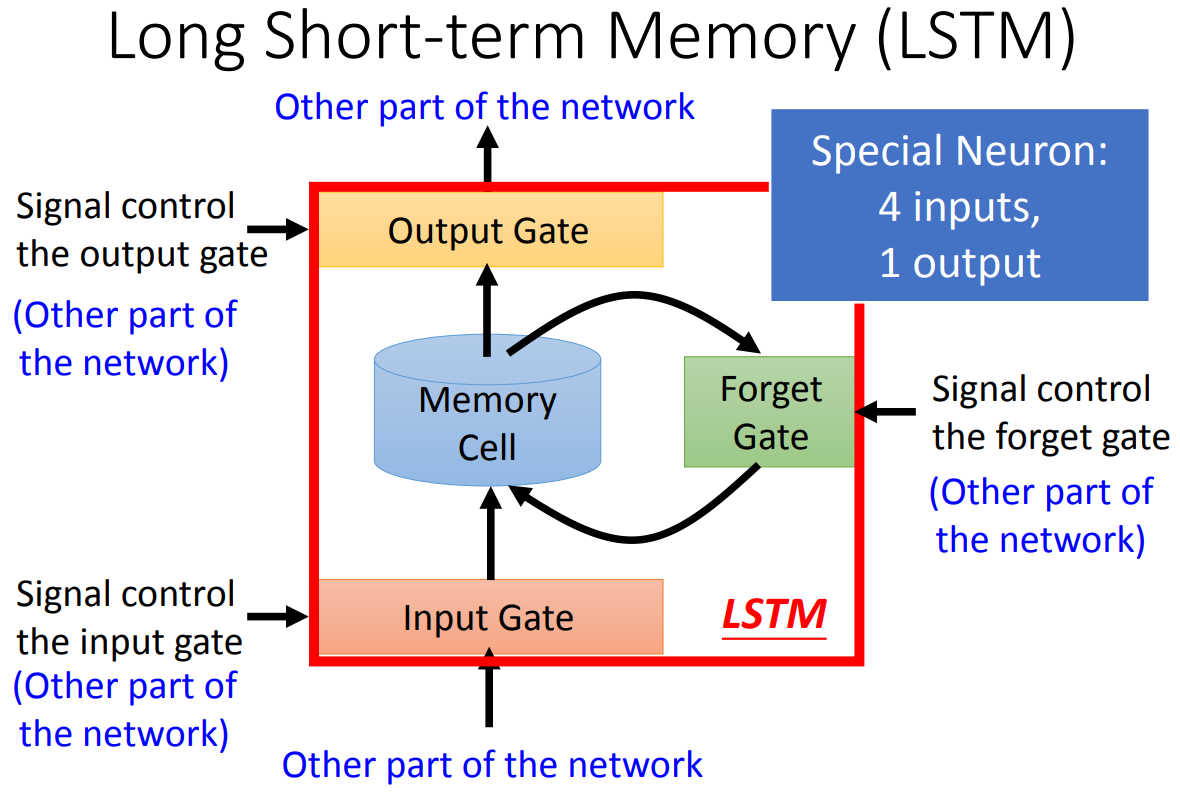
LSTM有四个输入，一个输出！

四个输入分别是：

• 模型的原始输入x
• 控制"输入门"的信号
• 控制"输出门"的信号
• 控制"遗忘门"的信号

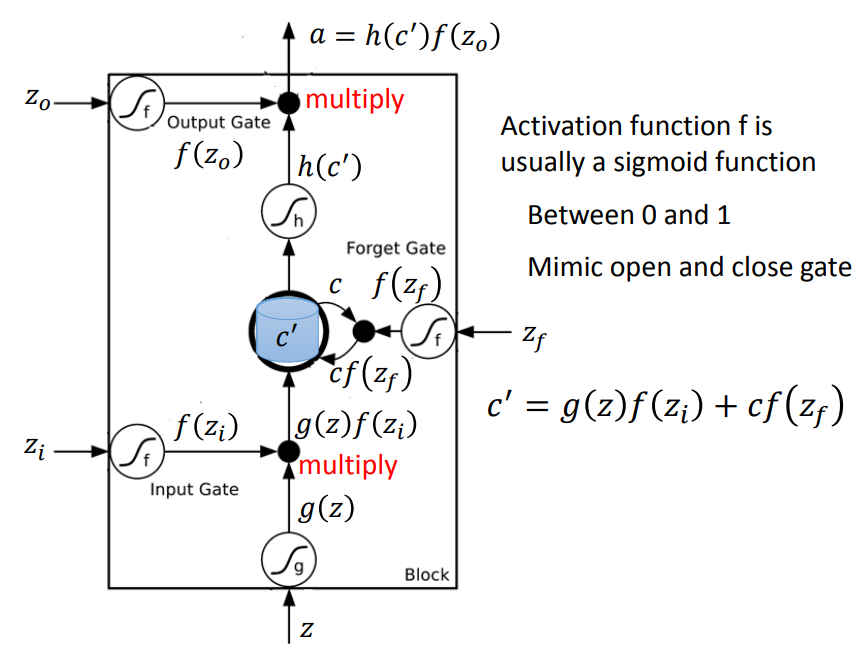
一个LSTM Block计算过程如上。

需要注意的是：

f通常使用sigmoid激活函数，使其值控制在0-1之间，表示不同门开闭的程度，1表示完全开放，0表示完全关闭。

此外，0虽然表示遗忘门关闭，但是只有遗忘门关闭时才会遗忘Memory Cell里面的讯息，这一点需要重点关注。

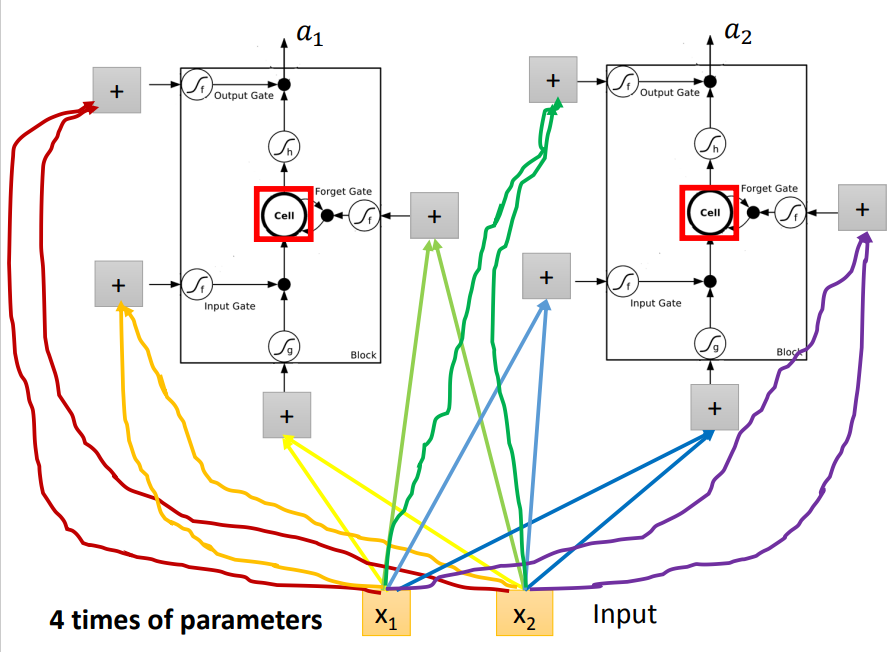
和普通的神经网络相比，我们可以把每一个LSTM Block视为一个Neuron，不同的是，每一个input需要乘以不同的weight得到4个不同的scalar，分别作为LSTM Block的4个输入；

因此，参数量相当于Fully-Connected Network的4倍！

用向量表示：

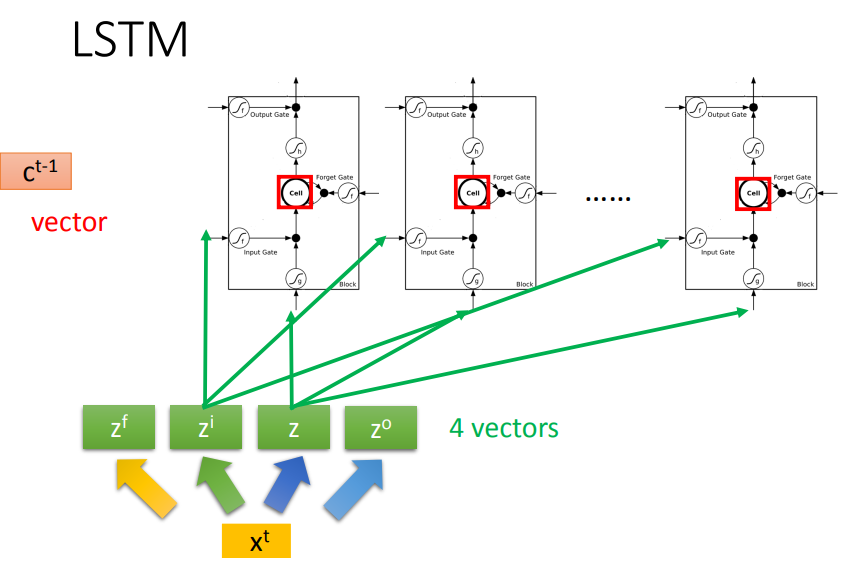
具体来说，就是将我们的输入乘上不同的权重矩阵得到四个向量，分别对应四个信号。

我们传给第一个LSTM Block的是四个向量中每个向量的第一个维度，传给第二个LSTM Block的是四个向量中每个向量的第二个维度，依次类推...

在(t-1)时刻所有的Memory Cell的值拼在一起就是c^t-1

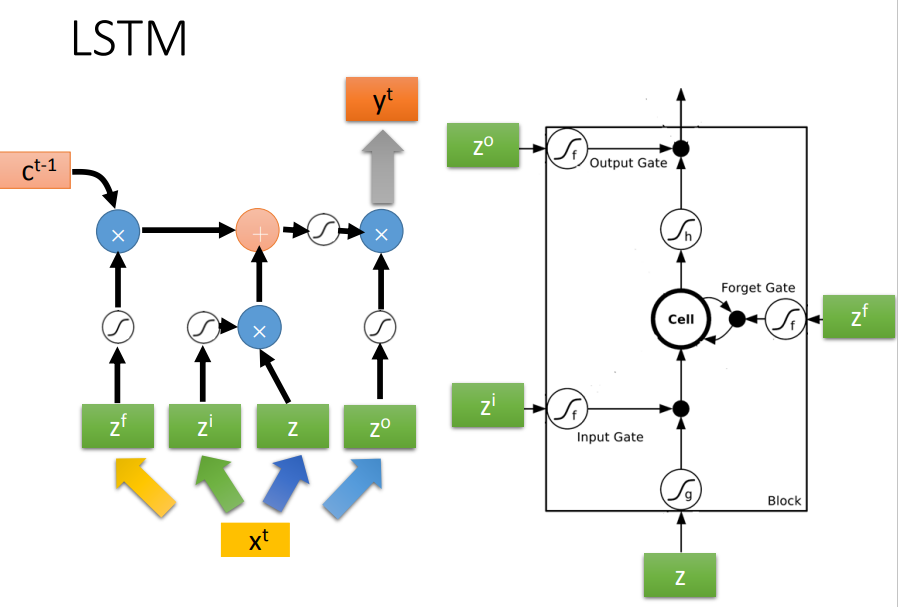
上图是具体计算流程！

之前一直有一个问题困扰我，就是我们输入的长度有多长，不就应该有多少个Block吗？(换句话说，如果模型的输入是一个one-hot编码的向量，长度为100，那么LSTM的Hidden_size不就应该也是100吗？)

我尝试分析了一下不同矩阵的维度：

假设我们的输入x^t的形状为Lx1，权重矩阵W的形状为NxL，由z=Wx^t+b我们可以知道z的形状为Nx1，

我们给每个Block的只是z的其中一个维度，因此，N的大小决定了应该有多少个Block！

可以理解为：我们将输入向量通过线性组合将其长度进行了变换，接着将变换后的该维度的每一个值输入到LSTM Block中，向量的长度变换成多少是可调(N可调)的，因此Block的数量也就是可调的。

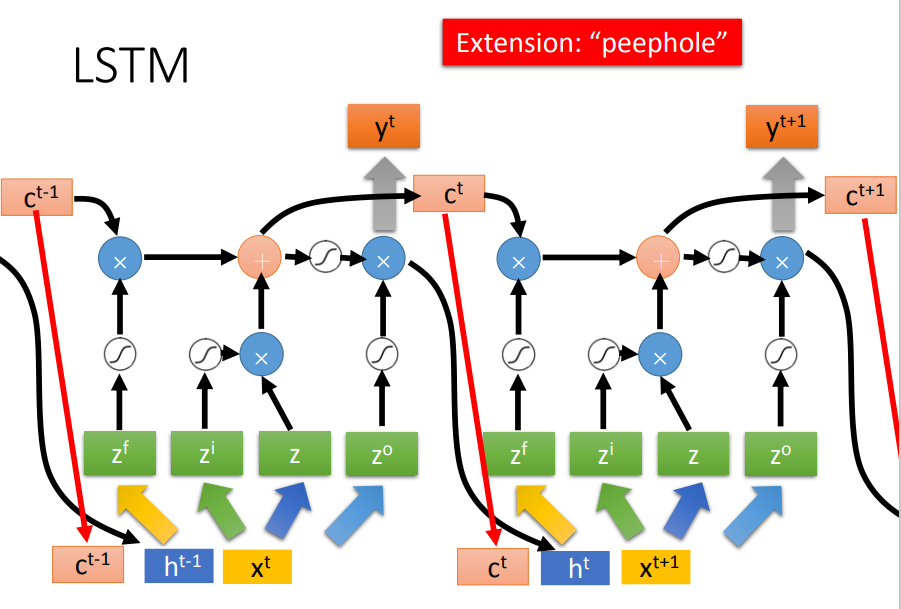
LSTM要比想象中的更加复杂。

实际上，在某一时刻的输入不仅包含t时刻的原始输入，还包括了上一时刻的输出，以及上一时刻Memory Cell的值！

 

续：李宏毅机器学习——循环神经网络(二)_循环神经网络 愤怒的_愤怒的可乐的博客-CSDN博客

 

---

END