PyTorch LSTM：权威指南

PyTorch LSTM：权威指南 | cnvrg.io

在这篇文章中，你将了解被称为 "长短时记忆 "或LSTM的特殊类型的神经网络。这篇文章分为4个主要部分。

1. 什么是顺序数据？

2. LSTM的重要性（传统神经网络的限制是什么，LSTM是如何克服这些限制的）。

   在本节中，你将了解传统的神经网络和循环神经网络及其缺点，并了解LSTM或长短时记忆是如何克服这些缺点的。

3. LSTM的数学直觉

4. 在PyTorch中的实际实现

什么是序列数据？

如果你从事数据科学工作，你可能已经知道，LSTM适合于数据为连续格式的顺序任务。让我们先来了解一下什么是顺序数据。

通俗地讲，顺序数据是指有顺序的数据。换句话说，它是一种数据的顺序很重要的数据。让我们通过例子来看看一些常见的顺序数据类型。
1.语言数据/一句话
例如 "我的名字是艾哈迈德"，或 "我在踢足球"。在这类例子中，你不能把顺序改为 "名字是我的阿迈德"，因为正确的顺序对句子的含义至关重要。

2.时间序列数据

例如，A公司每年的股票市场价格。在这种数据中，你必须逐年检查，找到一个顺序和趋势 - 你不能改变年份的顺序。

3.生物数据
例如，一个DNA序列必须保持顺序。

如果你观察，顺序数据在我们周围随处可见，例如，你可以看到音频是一个声波的序列，文本数据等。这些都是一些常见的顺序数据的例子，必须保持其顺序。长期以来的实验证明，传统的神经网络，如密集型神经网络，并不适合这些任务，无法保存序列。因此，你需要某种能够保存数据顺序的架构。
下一节将介绍传统神经网络架构的局限性，以及循环神经网络的一些问题，这将建立在对LSTM的理解之上。

LSTM的重要性

为了掌握LSTM的概念和重要性，你需要了解我们为什么需要LSTM。其他神经网络架构的局限性是什么，使我们觉得我们需要另一个适合处理连续数据的架构。

为此，你还需要了解递归神经网络（RNN）的工作和缺点，因为LSTM是RNN的一个改良架构。如果你对递归神经网络了解不多，不要担心，本文将在后面更详细地讨论其结构。

传统神经网络的问题

首先，让我们看一下下面的图片，以了解一个简单的神经网络的工作。

这张图片显示了一个简单的神经网络的工作，其中X是输入，ŷ是通过数学计算产生的输出。这是一个简单的 "一对一 "神经网络。同样，你也可以有一个多对多的神经网络或一个密集连接的神经网络，如下图所示

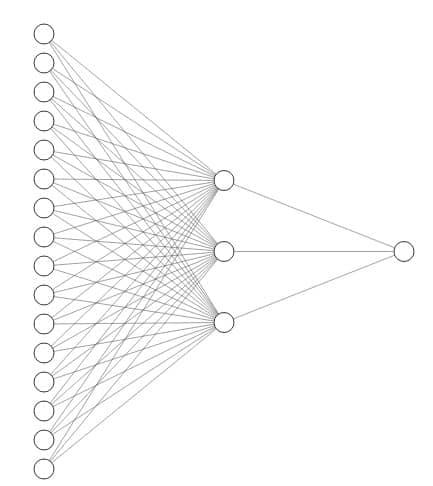
虽然这些网络比传统的机器学习算法表现更好，但它们有几个缺点。其中之一，当然是连续的数据。传统神经网络的其他缺点是：

1. 他们有一个固定的输入长度
2. 他们不能记住数据的顺序，也就是说，顺序并不重要。
3. 不能跨序列共享参数

让我们简单看一下这些问题，然后再深入挖掘RNN。

这里讨论的第一个问题是，它们有一个固定的输入长度，这意味着神经网络必须接受一个长度相同的输入。现在对于一个正常的顺序数据集，如一个国家每年的GDP，这个问题不是什么大问题，因为它们有相同数量的特征。但在处理语言等数据时，这个问题就出现了，因为每个句子的长度是不同的。例如,["Hello", "How", "are", "you]是一个长度为4的向量，而["My", "Name", "is", "Ahmad", "and", "I", "am", "sleeping"]是一个有9个单词的向量。这是一个严重的问题，具有很大的局限性。虽然科学家们在普通的神经网络中发现了一些变通方法，但对于高水平的模型来说，它们的表现并不理想。

传统神经网络的第二个限制是，它们不能记住数据的顺序，或者说顺序对它们来说并不重要。让我们通过一个例子来了解这个问题。

假设你有一个句子是 "我是艾哈迈德，不是哈桑"，另一个句子是 "我是哈桑，不是艾哈迈德"。传统的神经网络对这些句子的处理是一样的，因为两个句子都有相同的词。但是，我们知道，在这种情况下，顺序是非常重要的，完全改变了单词的含义。

这个问题的另一个例子显示在这个图中。

现在，传统神经网络的第三个限制是，它们不能在整个序列中共享参数。因此，为了理解这个问题，让我们拿一个句子 "你叫什么名字？我的名字是艾哈迈德"。现在，你会希望网络能把常见的词处理成相同的。在这种情况下，"名字 "应该有共享参数，而神经网络应该能够分辨出 "名字 "在一个序列中出现了多少次。不幸的是，传统的神经网络不能识别这种类型的模式，这使得它不适合于特定的机器学习解决方案。

正如你所看到的，这些限制使一个简单的神经网络不适合连续的任务。在处理与语言有关的任务或具有可变输入的任务时，这尤其具有局限性。

现在让我们来看看一些重要的要求，这些要求是顺序任务的必修课。

1. 该模型应能处理可变长度的序列
2. 可以跟踪长期的依赖关系（将在后面讨论）。
3. 保持有关序列的信息
4. 在整个序列中共享参数。
   现在我们来讨论一下RNN，即循环神经网络。RNN最初是为了满足传统神经网络无法满足的要求而设计的。

什么是递归神经网络？

RNN或递归神经网络，最初是为了处理传统神经网络在处理连续数据时的一些缺陷而设计的。

让我们将循环神经网络的结构与简单的神经网络作一比较。

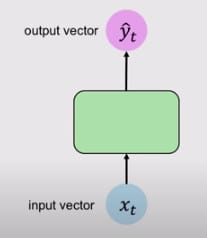
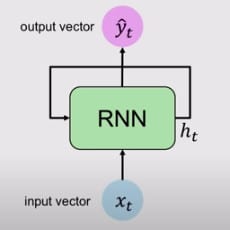
在这里你可以看到，简单神经网络是单向的，这意味着它有一个单一的方向，而RNN，在它里面有循环，以保持时间戳t的信息，这就是RNN被称为 "循环 "神经网络的原因。这种循环保留了序列上的信息。现在，让我们更深入地了解在引擎盖下发生了什么。

一个简化的解释是，在每个时间戳上都有一个递归关系来处理一个序列。

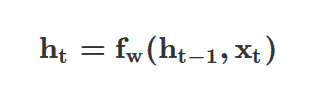
其中ht是当前的细胞状态，fw是一个以权重为参数的函数，ht-1是上一个或最后一个状态，Xt是时间戳t的输入矢量。这里需要注意的是，你在每个时间戳都使用相同的函数和参数集。

现在，它没有忽略以前的时间戳（或序列的顺序），你能够通过ht-1来保持它们，ht-1是帮助更新当前时间戳的以前的时间戳。

现在让我们进一步深入探讨一下。

鉴于输入矢量Xt，RNN应用一个函数来更新其隐藏状态，这是一个标准的神经网络操作。

正如你在上面的公式中看到的，你把输入矢量Xt和先前的状态ht-1都输入到函数中。这里你会有两个独立的权重矩阵，然后将非线性（tanh）应用于输入Xt和先前状态ht-1的总和，再与这两个权重矩阵相乘。最后，你会得到时间戳为t的输出向量ŷt。

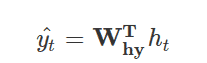
上述函数是这个内部状态的修改、转换版本，其结果只是与另一个权重矩阵相乘。这就是RNN如何更新其隐藏状态和计算输出的简单方法。

让我们加班展开RNN的循环，以获得更好的理解。下图会让您更好地了解如何在RNN内部展开循环。

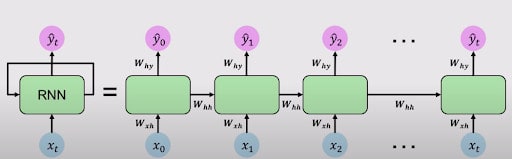
以上，你可以看到，你在每个时间戳上添加输入，并在每个时间戳上生成输出ŷ。如前所述，你将在每个时间戳使用相同的权重矩阵。而且，作为提醒，Whh是权重矩阵，你通过它来更新之前的状态，如上面的方程式所示，在图中可以看到。Wxh是在每个时间戳应用于输入值的权重矩阵。为什么应用于输出的权重矩阵是ŷ？

从这些输出ŷ0, ŷ1, ŷ2, ...., ŷt，你可以计算出每个时间戳t的损失L1, L2, ..., Lt。这将完成前向传递或前向传播，完成RNN的部分。现在让我们快速回顾一下RNN的工作。

1. RNN通过输入和先前的状态更新隐藏状态
2. 通过一个简单的神经网络操作计算输出矩阵，即W x h
3. 返回输出并更新隐藏状态

你可以结合起来，取所有这些损失的总和，计算出一个总的损失L，通过它可以向后传播，完成反向传播。下面是RNN中反向传播的工作原理的可视化表示。

RNNs中的反向传播与简单神经网络中的反向传播工作类似，其主要步骤如下。

• 前馈传球
• 用每个参数取损失的导数
• 转移参数以更新权重并最小化损失.

如果你仔细看上图，你可以看到它的运行与一个简单的神经网络相似。它完成了一个前馈通道，计算每个输出的损失，获取每个输出的导数，并向后传播以更新权重。由于错误是在每个时间戳计算和反向传播的，这也被称为 "通过时间反向传播"。

计算梯度需要很多Whh的因子，再加上重复的梯度计算，这使得它有点问题。在RNN中可能出现2个主要问题，LSTM有助于解决这些问题：

1. 爆炸性的梯度
2. 消失的梯度

爆炸性梯度是一个问题，当许多涉及重复梯度计算的数值（如权重矩阵，或梯度本身）大于1时，这个问题被称为爆炸性梯度。在这个问题中，梯度变得非常大，而且很难对其进行优化。这个问题可以通过一个被称为 "梯度切割 "的过程来解决，它基本上是将梯度缩减到较小的数值。

当参与重复梯度计算的许多数值（如权重矩阵，或梯度本身）太小或小于1时，就会出现消失的梯度。在这个问题中，当这些计算重复发生时，梯度变得越来越小。这可能是一个大问题。让我们看一个例子。

假设你有一个你想解决的单词预测问题，"云彩在____"。现在，由于这不是一个长的序列，RNN可以很容易地记住这一点，与每个词相关的权重（每个词在时间戳上输入）不会太大，也不会太小。但是，当你有一个大的序列，例如、

"我叫艾哈迈德，我住在巴基斯坦，我是一个好孩子，我在五年级，我是_____"。现在RNN要预测这里的 "巴基斯坦 "这个词，它必须记住巴基斯坦这个词，但由于这是一个很长的序列，而且有消失的梯度，即 "巴基斯坦 "这个词的权重非常小，所以模型将很难预测这里的 "巴基斯坦 "这个词。这也被称为长期依赖性的问题。.

现在你可以看到为什么有小数值的计算（梯度消失）是一个大问题。

这个问题可以通过3种方式解决：。

1. 激活函数（ReLU而不是tanh）。
2. 权重初始化
3. 不断变化的网络结构

本节将重点讨论第三种解决方案，即改变网络结构。在这个解决方案中，你修改了RNN的架构，并使用更复杂的递归单元与盖茨，如LSTMs或GRU（门控递归单元）。GRU超出了本文的范围，所以我们将只深入研究LSTM。

长短时记忆（LSTMs）

LSTM是一种特殊的神经网络，其性能与递归神经网络相似，但比RNN运行得更好，并进一步解决了RNN在长期依赖性和梯度消失方面的一些重要缺陷。LSTM最适合于长期依赖性，你将在后面看到它们如何克服梯度消失的问题。

LSTM的主要思想是，他们引入了自我循环，以产生梯度可以长期流动的路径（意味着梯度不会消失）。这个想法是最初长短时记忆的主要贡献（Hochireiter和Schmidhuber，1997）。后来，又做了一个重要的补充，使这个自循环的权重以环境为条件，而不是固定的。这可以帮助改变整合的时间尺度。这意味着，即使LSTM有固定的参数，整合的时间尺度也可以根据输入序列而改变，因为时间常数是由模型本身输出的。

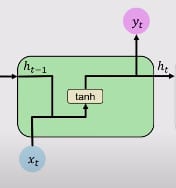
让我们快速回顾一下RNN的单个块。

• 带有tanh激活的单计算层
• ht是前一个细胞状态ht-1和当前输入Xt的函数，如上式所示。

下面是一个单一RNN单元的工作流程。

现在让我们来关注一下LSTM模块。LSTM模块包含控制信息流的计算块。这些涉及更多的复杂性，与RNN相比，有更多的计算。但作为一个结果，LSTM可以通过许多时间戳来保持或跟踪信息。在这个架构中，不是有一个，而是有两个隐藏状态。

在LSTM中，有不同的交互层。这些层相互作用，选择性地控制信息在细胞中的流动。

LSTM背后的关键构件是一个被称为门的结构。信息通过这些门被添加或删除。门可以选择性地让信息通过，例如通过西格莫德层，以及点状乘法，如下图所示。

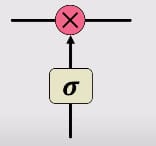
一个门由一个神经网层组成，就像一个sigmoid，和一个上图中红色显示的点状乘法。Sigmoid是强迫输入在0和1之间，这决定了通过门时有多少信息被捕获，以及通过门时有多少信息被保留。例如，0意味着没有信息被保留，1意味着所有信息被保留。

让我们更深入地了解LSTM的工作。

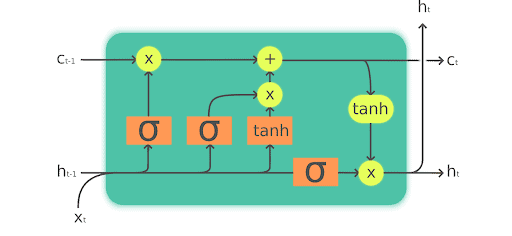
LSTM如何在4个简单的步骤中工作：

1.遗忘门

这是通过遗忘门完成的。遗忘门的主要目的是决定LSTM应该保留或携带哪些信息，以及它应该丢弃哪些信息。这是先前的内部状态ht-1和新输入的Xt的函数。.

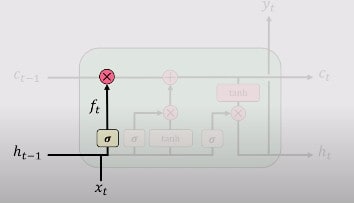
出现这种情况是因为在一个序列或一个句子中，并非所有的信息都需要是重要的。有些信息相对更重要，而有些信息则根本不重要。比如说"我的名字是Ahmad"。在这个句子中，LSTM要存储的重要信息是说这句话的人的名字是 "Ahmad"。但一个句子也可以有一段不相关的信息，如 "我的朋友叫阿里。他是个好孩子。他在读四年级。我父亲在睡觉。阿里是一个敏锐而聪明的男孩"。在这里，你可以看到它在谈论 "阿里"，并有一个关于我父亲的不相关的句子。这是一个例子，LSTM可以决定发送什么相关信息，以及不发送什么。

这个遗忘门用fi(t)表示（对于时间步长t和单元i），它在0和1之间设置这个权重值，决定发送多少信息，如上所述。让我们来看看这个方程式。

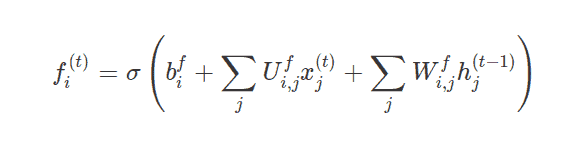
其中x(t)是当前的输入向量，h(t)是当前的隐藏状态，包含所有LSTM单元的输出，bf、Uf、Wfare分别是遗忘门的偏差、输入权重和循环权重。

2.执行计算并存储相关的新信息

当LSTM决定了哪些相关信息需要保留，哪些需要抛弃时，它就会进行一些计算来存储新的信息。这些计算是通过输入门或有时被称为外部输入门进行的。为了更新内部细胞状态，你必须在之前做一些计算。首先，你要把之前的隐藏状态，以及当前的输入与偏置传给一个sigmoid激活函数，该函数通过在0和1之间的转换来决定哪些值需要更新。

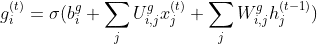
3.使用这2个步骤，有选择地更新其内部状态

由于现在有足够的信息，这次为了更新它的内部状态，你会有条件的自循环权重f(i)t。首先，我们将之前的单元格状态sit-1与遗忘向量（或门）做点状相乘，然后从输入门git中获取输出并将其相加。然后我们进行简单的神经网络操作。

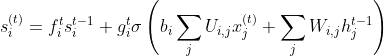
其中b、U和W分别表示偏置、输入权重和进入LSTM单元的递归权重。你会发现，这个内部状态也被表示为ct，如下图所示，来自麻省理工学院深度学习班.

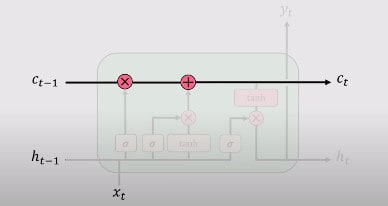
4.输出门

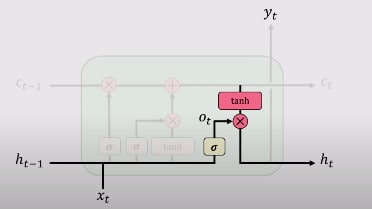
最后，你将通过输出门进行输出。这个输出门控制哪些信息要被编码到细胞状态中，作为下一个时间戳的输入发送给网络。这个隐藏状态（被发送到下一个网络）也被用于预测。它的工作原理如下。你把从第3步得到的新修改的状态传给tanh函数。然后将输出与在当前时间戳对以前的输出和输入进行的标准神经网络操作的sigmoid输出相乘。该输出用hit表示

方程如下：

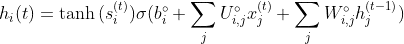
从图形上看，你可以从这张图片中看到，它取自麻省理工学院的深度学习课程，可在YouTube上免费获得.

LSTM的一个基本属性是，门控和更新机制的作用是创建内部的细胞状态Ct或St，允许不间断的梯度工作流随着时间推移。你可以把它看作是一条细胞状态的高速公路，梯度可以不间断地流动。这使我们能够消除消失的梯度问题，如标准或香草RNN中所示。

长短时记忆的变体

长短时记忆有不同的变体，而我所解释的那个是很常见的。并非所有的LSTM都像上面的例子一样，你会发现在数学公式和LSTM细胞的工作中存在一些差异。不过，这些差异并不是主要的差异，如果你清楚地了解它们，你也可以很容易地理解它们。

下面是一个基本的LSTM结构的图形描述，以帮助人们更深入地理解上面定义的概念。

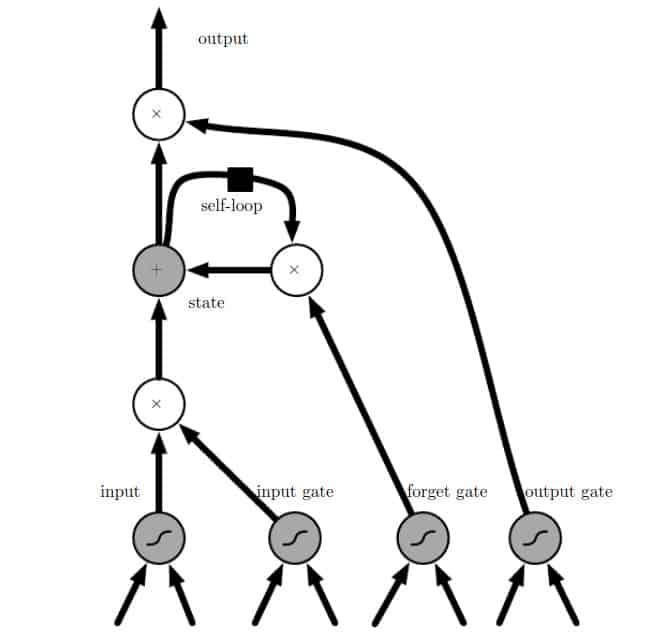
现在让我们快速回顾一下LSTM的关键概念。

1.LSTM可以保持一个独立的细胞状态，而不是它们所输出的东西。

2.他们使用闸门来控制信息的流动

3.遗忘门是用来摆脱无用的信息的

4.存储当前输入的相关信息

5.有选择地更新细胞状态

输出门返回细胞状态的过滤版本

不间断梯度流的时间反向传播

LSTM的反向传播工作与RNN部分的描述类似。

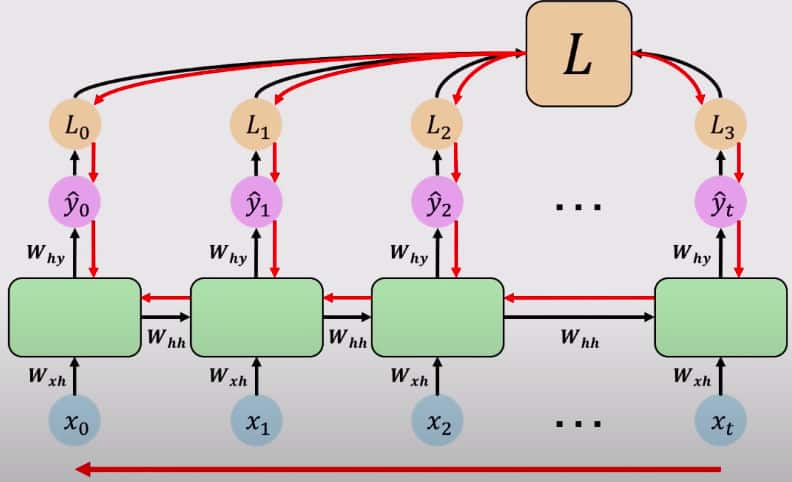
接下来，取总损失的总和，把它们加起来，并随着时间的推移向后流动。如果你想得到一个数学导数过程，我向你推荐这篇文章和这里同一文章的升级版。他们在计算反向传播所需的所有数学导数方面做得很好。

在PyTorch中的实际实现

让我们看看星巴克股票市场价格的真实例子，这是一个序列数据的例子。在这个例子中，我们将使用Python和PyTorch进行一个简单的LSTM模型来预测星巴克股票价格的波动。

让我们先加载数据集。你可以从这个链接中下载该数据集。你可以用pandas加载它。

输入numpy作为np
输入pandas作为pd

df = pd.read_csv('SBUX.csv', index_col = 'Date', parse_dates=True)

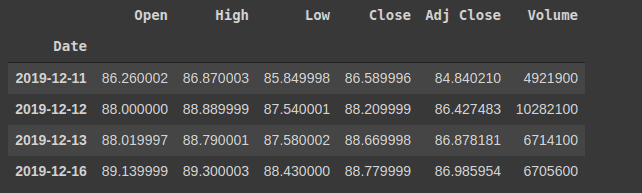
你可以通过以下方式检查数据集的头部

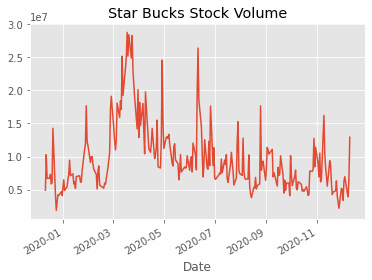
现在，你可以绘制标签栏，用时间框架来检查股票量的原始趋势。

plt.style.use(‘ggplot’)

df['Volume'].plot(label='CLOSE', title='星巴克股票成交量')

由于本文更侧重于PyTorch部分，我们不会深入到进一步的数据探索，而只是深入到如何建立LSTM模型。在制作模型之前，你必须做的最后一件事是为模型准备数据。这也被称为数据预处理。

让我们把数据和标签从一个数据框架中分离出来。

X = df.iloc[:, :-1]
y = df.iloc[:, 5:6] 

由于这不是一篇专注于数据预处理的不同技术的文章，你将对特征使用StandardScaler，对输出值使用MinMaxScaler（对0和1之间的值进行缩放）。请注意，这是一个回归问题，所以对你的输出进行缩放是非常有益的，否则你将会面临巨大的损失。

from sklearn.preprocessing import StandardScaler, MinMaxScaler
mm = MinMaxScaler()
ss = StandardScaler()


X_ss = ss.fit_transform(X)
y_mm = mm.fit_transform(y) 

这将转换和缩放数据集。下一件事是将数据集分成两部分。一部分用于训练，另一部分用于测试值。由于它是连续的数据，而且顺序很重要，你将把前200行用于训练，53行用于测试数据。你会注意到，你可以使用LSTM在如此低的数据量上做出一个非常好的预测.

#first 200 for training

X_train = X_ss[:200, :]
X_test = X_ss[200:, :]

y_train = y_mm[:200, :]
y_test = y_mm[200:, :] 

接下来，你可以打印出训练和测试数据的形状进行确认。

print("Training Shape", X_train.shape, y_train.shape)
print("Testing Shape", X_test.shape, y_test.shape) 

如果你在PyTorch中进行了一段时间的编程，你应该知道在PyTorch中，你所处理的都是张量，你可以把它看作是numpy的一个强大版本。所以你必须把数据集转换为张量。

让我们先导入重要的库。

import torch #pytorch
import torch.nn as nn
from torch.autograd import Variable 

你可以通过这个简单的代码将Numpy数组转换为Tensors和Variables（可以进行区分）。

X_train_tensors = Variable(torch.Tensor(X_train))
X_test_tensors = Variable(torch.Tensor(X_test))

y_train_tensors = Variable(torch.Tensor(y_train))
y_test_tensors = Variable(torch.Tensor(y_test)) 

现在，下一步是要检查LSTM的输入格式。这意味着，由于LSTM是专门为顺序数据建立的，它不能接受简单的2-D数据作为输入。它们也需要有时间戳信息，因为我们讨论过，我们需要在每个时间戳都有输入。因此，让我们来转换数据集。

#reshaping to rows, timestamps, features

X_train_tensors_final = torch.reshape(X_train_tensors,   (X_train_tensors.shape[0], 1, X_train_tensors.shape[1]))


X_test_tensors_final = torch.reshape(X_test_tensors,  (X_test_tensors.shape[0], 1, X_test_tensors.shape[1])) 
print("Training Shape", X_train_tensors_final.shape, y_train_tensors.shape)
print("Testing Shape", X_test_tensors_final.shape, y_test_tensors.shape) 

现在，你可以开始了，是时候建立LSTM模型了。由于PyTorch是更加pythonic的方式，它的每个模型都需要继承自nn.Module的超类。

这里你已经定义了所有重要的变量和层。接下来，你将使用2个具有相同超参数的LSTM层相互堆叠（通过hidden_size），你已经定义了2个全连接层，ReLU层，以及一些辅助变量。接下来，你要定义LSTM的前向传递。

class LSTM1(nn.Module):
    def __init__(self, num_classes, input_size, hidden_size, num_layers, seq_length):
        super(LSTM1, self).__init__()
        self.num_classes = num_classes #number of classes
        self.num_layers = num_layers #number of layers
        self.input_size = input_size #input size
        self.hidden_size = hidden_size #hidden state
        self.seq_length = seq_length #sequence length

        self.lstm = nn.LSTM(input_size=input_size, hidden_size=hidden_size,
                          num_layers=num_layers, batch_first=True) #lstm
        self.fc_1 =  nn.Linear(hidden_size, 128) #fully connected 1
        self.fc = nn.Linear(128, num_classes) #fully connected last layer

        self.relu = nn.ReLU()
    
    def forward(self,x):
        h_0 = Variable(torch.zeros(self.num_layers, x.size(0), self.hidden_size)) #hidden state
        c_0 = Variable(torch.zeros(self.num_layers, x.size(0), self.hidden_size)) #internal state
        # Propagate input through LSTM
        output, (hn, cn) = self.lstm(x, (h_0, c_0)) #lstm with input, hidden, and internal state
        hn = hn.view(-1, self.hidden_size) #reshaping the data for Dense layer next
        out = self.relu(hn)
        out = self.fc_1(out) #first Dense
        out = self.relu(out) #relu
        out = self.fc(out) #Final Output
        return out
 

这里你首先定义了隐藏状态和内部状态，初始化为零。首先，你要在LSTM中传递隐藏状态和内部状态，以及当前时间戳t的输入，这将返回一个新的隐藏状态、当前状态和输出。你将对输出进行重塑，使其能够传递给密集层。接下来，简单地应用激活，并将其传递给密集层，然后返回输出。

这就完成了Forward Pass和LSTM1类。你将在运行时训练模型时应用反向传播逻辑。

你可以通过打印模型看到模型的统计数据。

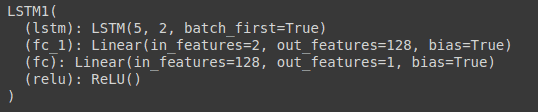
现在让我们定义一些重要的变量，你将会使用这些变量。这些是超参数，如历时数、隐藏大小等。

num_epochs = 1000 #1000 epochs
learning_rate = 0.001 #0.001 lr

input_size = 5 #number of features
hidden_size = 2 #number of features in hidden state
num_layers = 1 #number of stacked lstm layers

num_classes = 1 #number of output classes 
lstm1 = LSTM1(num_classes, input_size, hidden_size, num_layers, X_train_tensors_final.shape[1]) #our lstm class 
criterion = torch.nn.MSELoss()    # mean-squared error for regression
optimizer = torch.optim.Adam(lstm1.parameters(), lr=learning_rate) 

现在循环计算历时数，做正向传递，计算损失，通过优化器步骤改进权重。

for epoch in range(num_epochs):
  outputs = lstm1.forward(X_train_tensors_final) #forward pass
  optimizer.zero_grad() #caluclate the gradient, manually setting to 0
 
  # obtain the loss function
  loss = criterion(outputs, y_train_tensors)
 
  loss.backward() #calculates the loss of the loss function
 
  optimizer.step() #improve from loss, i.e backprop
  if epoch % 100 == 0:
    print("Epoch: %d, loss: %1.5f" % (epoch, loss.item())) 

这将启动1000个epochs的训练，并在每100个epoch时打印损失。

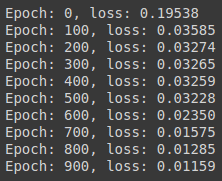
你可以看到，损失较少，这意味着它表现良好。让我们在数据集上绘制预测图，看看它的表现如何。

但在对整个数据集进行预测之前，你需要将原始数据集带入模型的合适格式，这可以通过使用上述类似代码来完成。

df_X_ss = ss.transform(df.iloc[:, :-1]) #old transformers
df_y_mm = mm.transform(df.iloc[:, -1:]) #old transformers

df_X_ss = Variable(torch.Tensor(df_X_ss)) #converting to Tensors
df_y_mm = Variable(torch.Tensor(df_y_mm))
#reshaping the dataset
df_X_ss = torch.reshape(df_X_ss, (df_X_ss.shape[0], 1, df_X_ss.shape[1])) 

现在你可以简单地通过正向传递对整个数据集进行预测，然后为了绘图，你将把预测结果转换为numpy，反向转换（记得你转换了标签来检查实际答案，你需要反向转换），然后绘图。

train_predict = lstm1(df_X_ss)#forward pass
data_predict = train_predict.data.numpy() #numpy conversion
dataY_plot = df_y_mm.data.numpy()

data_predict = mm.inverse_transform(data_predict) #reverse transformation
dataY_plot = mm.inverse_transform(dataY_plot)
plt.figure(figsize=(10,6)) #plotting
plt.axvline(x=200, c='r', linestyle='--') #size of the training set

plt.plot(dataY_plot, label='Actuall Data') #actual plot
plt.plot(data_predict, label='Predicted Data') #predicted plot
plt.title('Time-Series Prediction')
plt.legend()
plt.show() 

原文链接：https://cnvrg.io/pytorch-lstm/