绪论、概率论基础

绪论、概率论基础

1 绪论

1.1 数据信息知识

（1) DIKW知识链

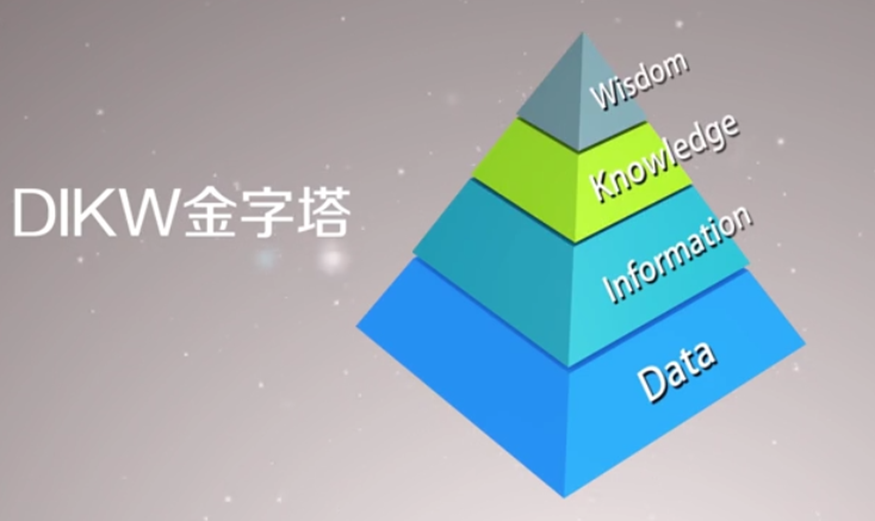
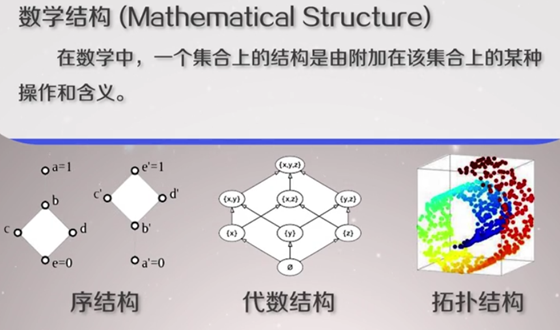
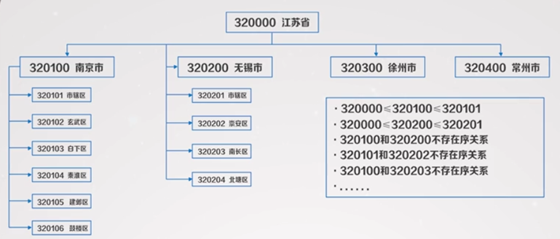
注：通过结构获得一定的信息

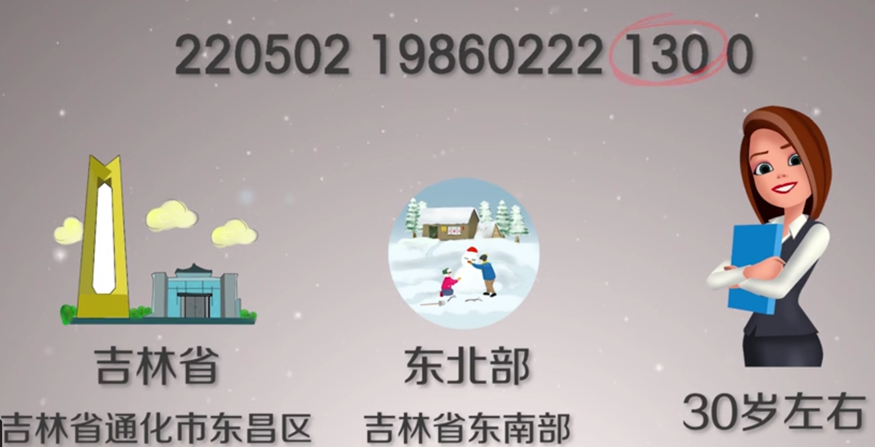
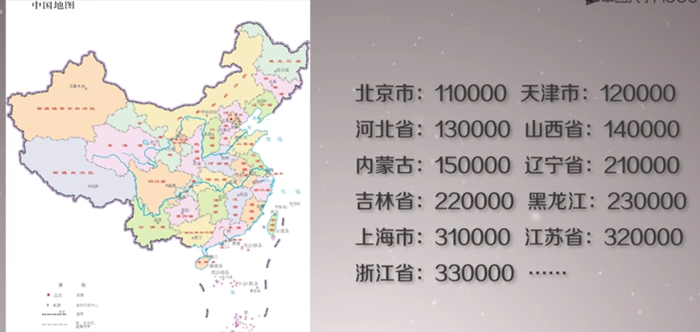
注：130表示同一标识地区同一天出生的顺序号，基数分配给男性，偶数分配给女性；最后一位是校验码，通过SO的标准计算（0-9、X）。

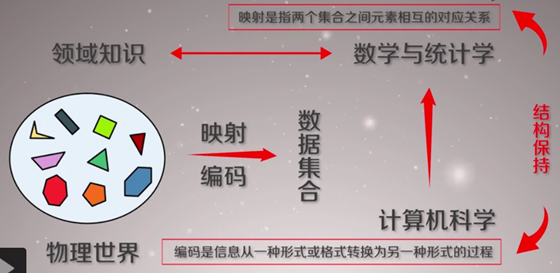
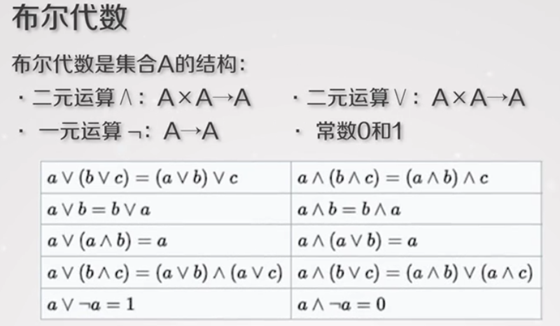
（2) 相关数学理论

注：集合论是研究集合（由一堆抽象对象构成的整体）的数学理论，包含集合和元素以及关系等最基本数学概念。

1.2 数据类型

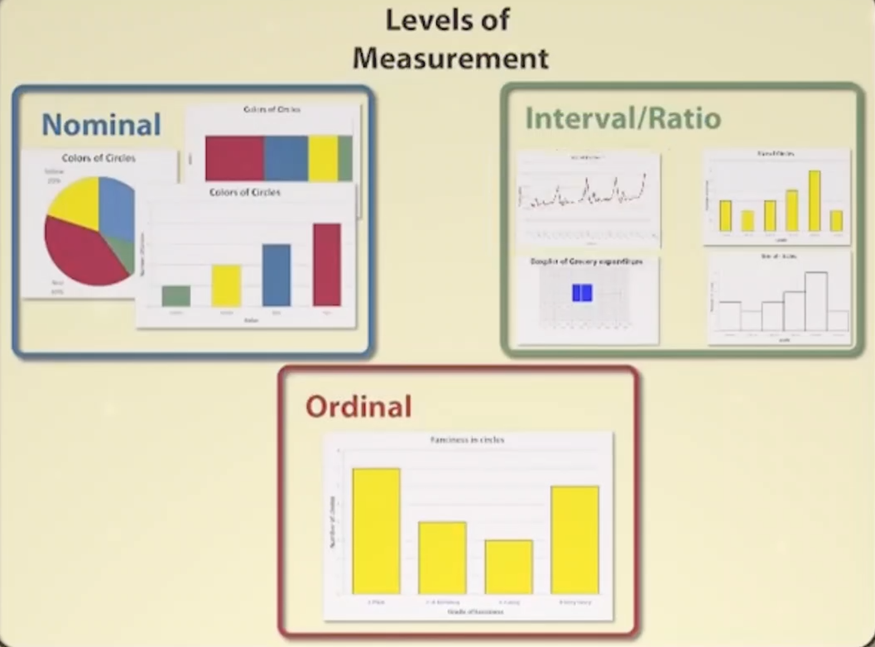
注：Nominal：饼图、柱状图、横向柱状图；

Ordinal：柱状图；

interval/Ratio：直方图，箱型图、折线图；

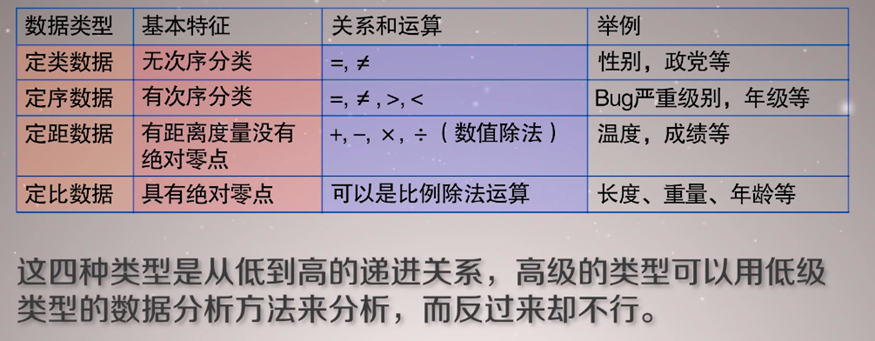
（1) 定类数据

注：我们比较不同程序语言，分别将C、C++、Java定义为1,2,3；也可定义为2,3,4.定类数据之间的数学关系就是等于（=）或者不等于（≠）。我们可以说Java≠C，但不能说Java>C

（2）定序数据

（3）定距数据

（4）定比数据

注：摄氏度0度不代表没有温度；

（5）小结

（6）其它数据类型

1.3 数据汇总

分类：

\1. 集中趋势度量（ Central Tendency）

\2. 离散趋势度量（Variation Tendency)

\3. 形态趋势度量

（1）集中趋势度量

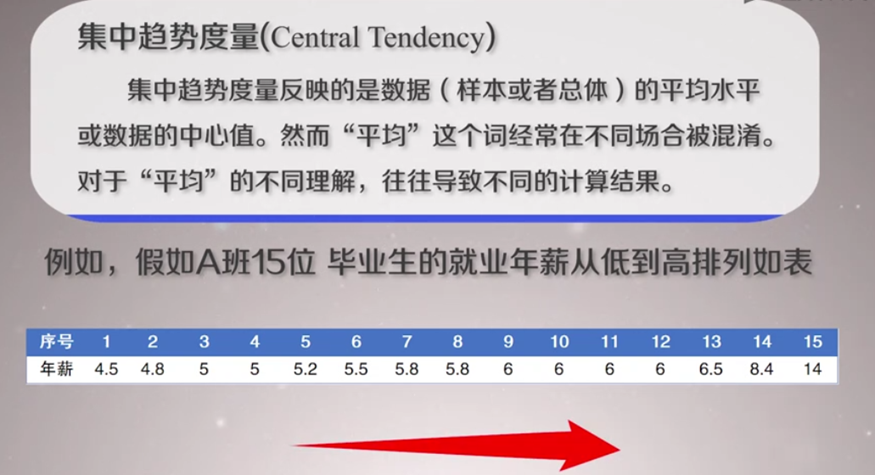
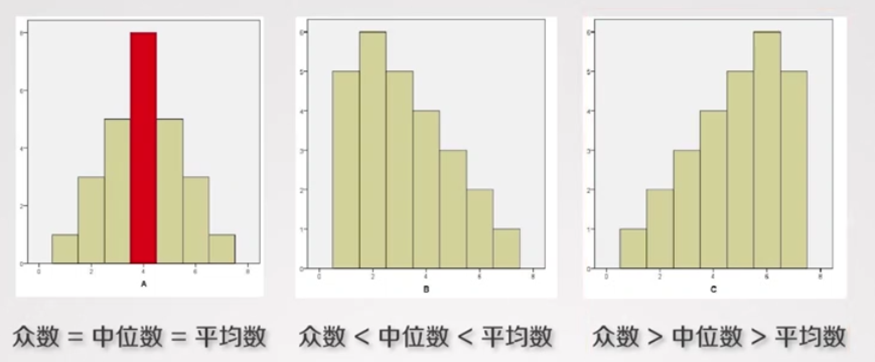
众数

中位数

四分位数

N分位数

（算数)平均数

缺点：易受极值的影响

求和稳定性

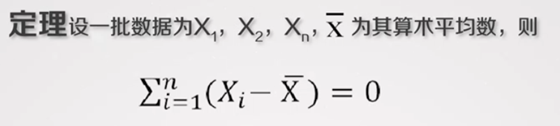
加权平均数

几何平均数

注：对数（几何平均数）→算术平均数

调和平均数

平方平均数

（2）离散趋势度量

全距

内距

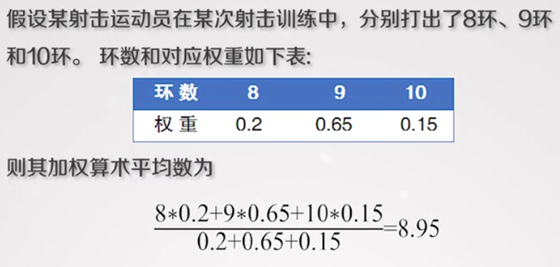
偏差平方和

注：为什么用算术平均值做偏差？算术平均数的偏差极小性

方差与标准差

在计算方差的时候，我们使用计算式，而不是定义式！

注：偏差方 = 平方的和-和的平方

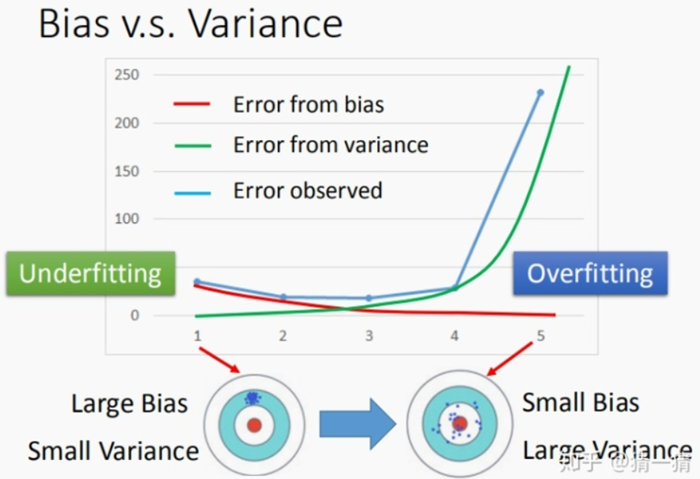
1.4数据科学不同角色

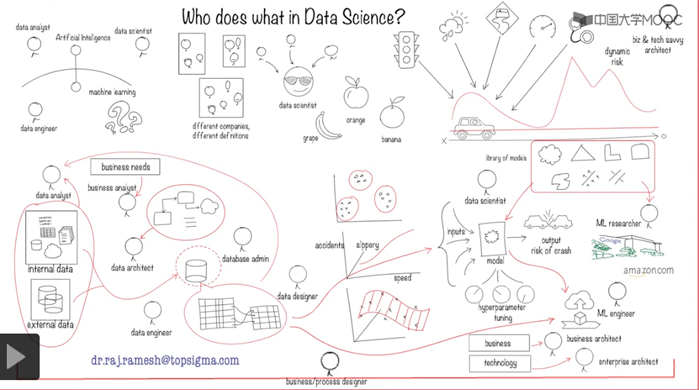
2 概率论基础

2.1 概率定义

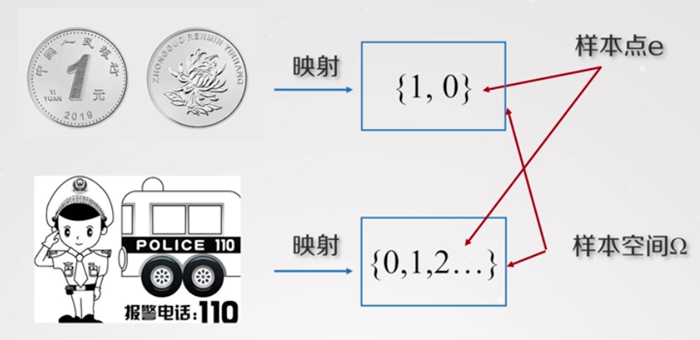
（1) 事件

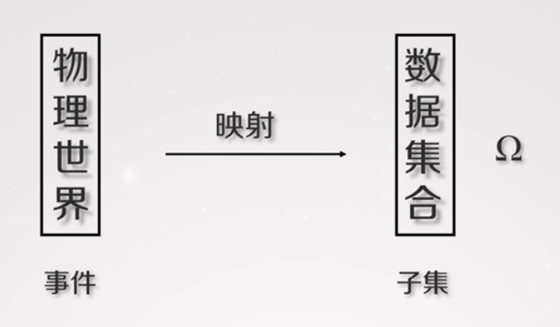
事件集合表示

事件的集合运算

事件发生的频率

（2）古典概率

定义

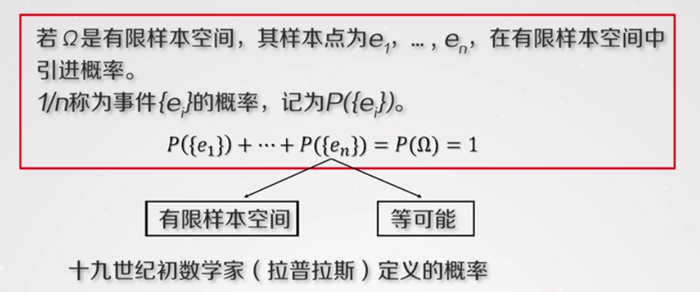
计算

（3）几何概率

示例

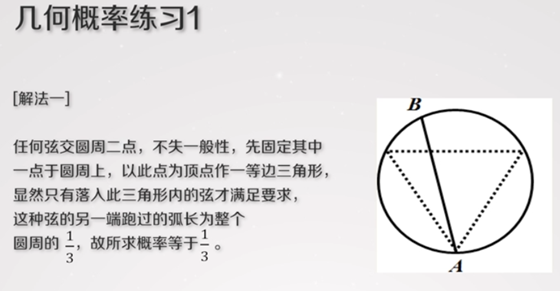
（4）概率的公理化定义

2.2 概率计算

条件概率

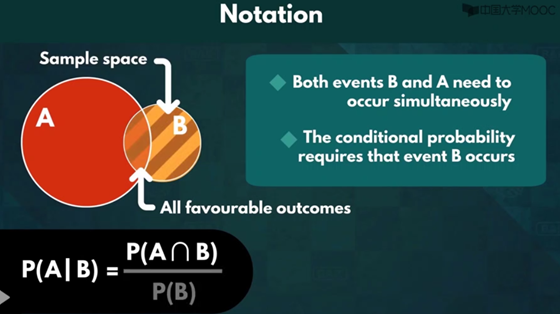
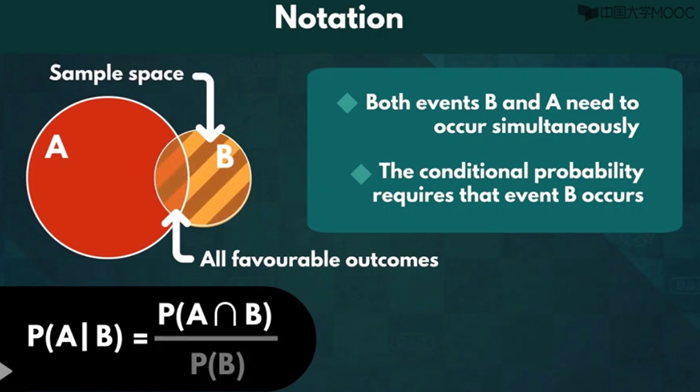
乘法公式

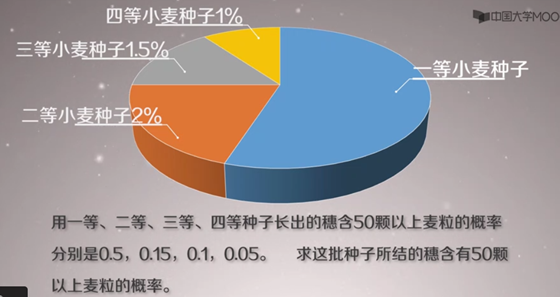
全概率公式

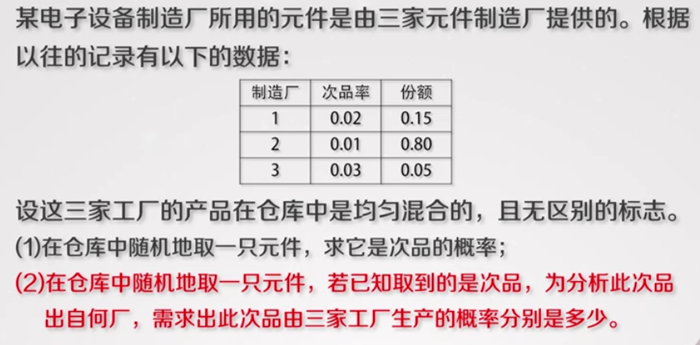
贝叶斯公式

独立性

2.3 随机测试示例

有放回抽样

无放回抽样