中国矿业大学数据结构实验(2)

A 子串个数

长度为\(n\)的字符串，其子串个数为\(\frac{n(n+1)}{2}+1\)

B KMP

KMP算法

给定一个模式串\(P\)和一个主串\(S\)，求模式串\(P\)在主串\(S\)中出现的位置

求\(next[]\)数组

\(next[i]\)表示\(P[1,i]\)中相等前后缀的最长长度,\(i\)扫描模式串，\(j\)扫描前缀

初始化\(next[1]=0\)，指针\(i = 2,j=0\)

每轮for循环，\(i\)向右走一步：

\((1)\)若\(P[i] \ne P[j+1]\)，则让\(j\)退回到能匹配的值，即\(j=next[j]\)，直到为\(0\)；

\((2)\)若\(P[i] = P[j+1]\)，则让\(j+1\)，指向匹配前缀的末尾；

\((3)\)\(next[i]=j\).

next[1] = 0;
int i = 2,j = 0;
for(i,j; i <= n ; i ++){
    while(j && P[i] != P[j+1]) j = next[j];
    if(P[i] == P[j+1]) j ++;
    next[i] = j;
}

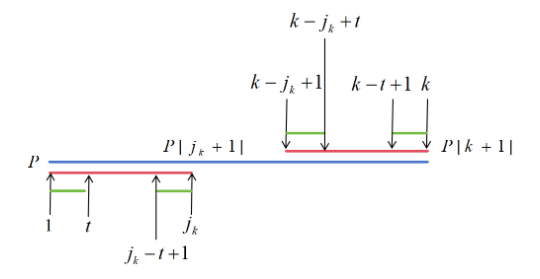
说明：假设第\(k+1\)轮循环开始时对应的\(j = j_k\)，由于前一次的操作，我们知道\(P[1,j_k]\)是已经匹配的最长前缀，即\(P[1,j_k]=P[k-j_k+1,k]\)，分情况讨论：

\((1)\)若\(P[j_k+1]=P[k+1]\)，说明\(P[1,j_k]+P[j_k+1]=P[k-j_k+1,k]+P[k+1]\)即\(P[1,j_k+1]=P[k-j_k+1,k+1]\)，故\(j_{k+1}=j_k+1\)；

\((2)\)若\(P[j_k+1]\ne P[k+1]\)，那么\(P[1,j_k]+P[j_k+1]\ne P[k-j_k+1,k]+P[k+1]\)，匹配长度无法增加\(1\)，而我们已知\([1,k]\)的\(next[]\)值，从之前的操作来看：\(j_k \in [1,k]\)，那么\(next[j_k]\)已知，令\(t = next[j_k]\)，则有\(P[1,t]=P[j_k-t+1]\).在第\(k\)轮循环后，\(P[1,j_k]=P[k-j_k+1,k]\)，那么\(P[k-j_k+1,k-j_k+t]=P[k-t+1,k]\)，所以证得\(P[1,t]=P[k-t+1,k]\)，比较形式，可得\(j_{k+1}=next[j_k]\)，当再次不匹配时，\(j_{k+1}=next[next[j_k]]\)，如此循环，直到\(j=0\)或者匹配为止.

模式串与主串匹配

双指针：\(i\)扫描主串，\(j\)扫描模式串，初始化\(i=1,j=0\)

每轮for循环，\(i\)向右走一步：

\((1)\)若\(S[i] \neq P[j+1]\)，让\(j\)回跳到能匹配的位置，找不到就回到\(0\)；

\((2)\)若\(S[i]=P[j+1]\)，让\(j\)向右走一步；

\((3)\)若匹配成功，则输出匹配位置

总共的时间复杂度：\(O(n+m)\)

#include <cstring>
#include <iostream>
using namespace std;

const int N = 1000010;
int m, n;
char S[N], P[N];
int nxt[N];

int main() {
    memset(S, 0, sizeof(S));
    memset(P, 0, sizeof(P));

    cin.getline(S + 1, N - 1);
    cin.getline(P + 1, N - 1);

    m = strlen(S + 1);
    n = strlen(P + 1);

    for (int i = 2, j = 0; i <= n; i++) {
        while (j && P[i] != P[j + 1]) j = nxt[j];
        if (P[i] == P[j + 1]) j++;
        nxt[i] = j;
    }

    bool found = false;
    for (int i = 1, j = 0; i <= m; i++) {
        while (j && S[i] != P[j + 1]) j = nxt[j];
        if (S[i] == P[j + 1]) j++;
        if (j == n) {
            printf("%d\n", i - n + 1);
            found = true;
            // j = nxt[j]; 
        }
    }

    if (!found) printf("0\n"); 
    return 0;
}

C

D

E

#include<iostream>
using namespace std;
int cnt = 0;

void dfs(int n, char x, char y, char z)
{
	if (n == 1) printf("%d %d %c->%c\n", ++cnt, n, x, z);
	else {
		dfs(n - 1, x, z, y);
		printf("%d %d %c->%c\n", ++cnt, n, x, z);
		dfs(n - 1, y, x, z);
	}
}


int main()
{
	int n;
	cin >> n;
	dfs(n, 'A', 'B', 'C');
	return 0;
}

FG

#include <iostream>
#include <vector>
using namespace std;

const int N = 27; 
vector<int> ch[N]; 
int din[N] = {0};  
int vis[N] = {0};  

int toi(char c) { return c - 'A' + 1; }
char toc(int a) { return 'A' + (a - 1); }

void dfs(int u, vector<char>& pre, vector<char>& post) {
    pre.push_back(toc(u));   
    for (int v : ch[u]) dfs(v, pre, post);
    post.push_back(toc(u));  
}

int main() {
    char x, y;
    while (cin >> x >> y) {
        int u = toi(x), v = toi(y);
        ch[u].push_back(v);
        din[v]++;
        vis[u] = vis[v] = 1;
    }


    int root = -1;
    for (int i = 1; i <= 26; i++) {
        if (vis[i] && din[i] == 0) {
            root = i;
            break;
        }
    }


    vector<char> preOrder, postOrder;
    dfs(root, preOrder, postOrder);


    for (char c : preOrder) cout << c << " ";

    for (char c : postOrder) cout << c << " ";


    return 0;
}