编写缓存友好型程序技巧
通过使用数据缓存加速程序
译者注:本文原始链接为<Make your programs run faster by better using the data cache>,翻译获得作者同意。本文中的一些策略只对大量数据处理有优化的可能,小量数据很可能带来性能下降。
通过使用数据缓存加速程序
开发者时刻面临着如何加速程序,其中最明显的是通过花哨的算法来降低复杂度。比如说将\(O(n^2)\) 复杂度的算法,使用 \(O(nlogn)\) 替换等等。这是很好的方法,但是并不是所有的程序都有更好的算法来优化。那么应该怎么办?是否存在一种方法来优化我们已存在的算法。事实上是存在的,它叫:底层优化(low-level optimizations)。
首先,先来了解一下底层优化的情况。底层优化关注于如何最好地利用底层架构的特殊性来获得更好的性能。这是这个系列的第一篇,将会涉及到底层优化。我们将在如何更好地利用内存缓存子系统上探索一系列的方法。对于熟悉现代多进程系统内存缓存原理的读者,可以调过 数据缓存 章节。
数据缓存
计算机系统通常包含处理器和内存。在现代计算机系是中内存是比处理器慢百倍的,因此处理器通常都要等待内存传输数据。聪明的硬件工程师想出了一个解决方案来抵消速度上差异:他们添加了一个很小的快速内存被称为缓存的东西,用以弥补不同的速度。当程序需要访问主存中的数据,它首先会检查数据是否已经在缓存中,如果在,它可以很快的获取数据。否则,计算机会牺牲一些处理器周期,等待主内存提供数据。
通常情况下,缓存存储器分为指令缓存存储器和数据缓存存储器。指令缓存器的目的是加速对指令的访问,数据缓冲器的目的是加快对指令所使用的数据的访问。这篇文章主要关注如何使用数据缓存器来加速程序。
为什么内存缓存可以使程序运行的更快?
那么,为什么增加缓存内存能起作用呢? 毕竟,程序可以在任何时候都可以访问任何内存位置,因此,这些数据不应该在缓存中。理论上是这样的,但在实践中,真正的程序几乎不会以随机方式访问内存。
有两个原则制约着现实世界的程序行为。第一条被称为时间局部性,即如果处理器目前正在访问某个内存地址,就很有可能在不久的将来访问这个内存地址(例如:循环中的计数器)。第二种被称为空间局部性,其含义是如果处理器目前正在访问某个内存地址,那么它很有可能会在不久的将来访问邻近的内存地址(例如:处理数组中的数据)。
数据缓存内部组织形式
现在让我们来看看缓存的内部情况。在现代计算机处理器中被分解为 Cache line,每个 Cache line 通常情况下是 64bytes 的大小。一个 Cache line 对应主存中 64byte 的内存块。获取 64byte 中的任意 1byte 数据,意味着需要加载整个 64byte 内存块到缓存中来。当 cache line 长时间没有使用或需要使用新的数据去替换,缓存将返回修改后的块到主存中去。这整个过程程序并不知道。
让程序运行更快的一些技巧
对数据缓存有了一定的了解后,让我们来看看如何将数据缓存相关的原理应用到你的程序中,从而使你的程序拥有更好的性能。
注意:下面每小节,我使用 C 写法的数组和 C++ 写法的数组(vector、array),以及 C 写法(struct)和 C++ 写法(class)的类。
当获取线性数据时,尽量使用vector和array
链表,hash maps,字典等,都是十分有用的数据结构,但是,它们都不是缓存优化的。在这些数据结构中遍历,将会带来很大的缓存丢失。如果,当前程序性能是最重要的因素,那么将这些数据结构转为数组。 如果这是不可能的,尝试将数组的缓存效率和其他数据的灵活性结合起来。Gap_buffer 是这种结合的很好例子。它将链表结构和数组结构结合,这使得其具有卓越的缓存效率和较低代价的元素添加和删除。另一个例子是 Judy_array ,稀疏数组的树形实现,同样的拥有很低代价的元素插入和删除并且缓存友好。
经常访问的数据,在内存中应当是相邻的
如果有几个变量被一起访问,它们应该被逐一声明。这就增加了另一个变量在处理器访问后已经在缓存中的可能性。因为在处理器访问了第一个变量之后,另一个变量已经在缓存中了。从而避免了缓冲区的缺失。
考虑下面的类:
class free_memory_list {
void* head; /// Pointer to the beginning of the list
Statistics statistics; /// Statistics about list usage
int count; /// Number of elements in the list
Allocator* base_allocator; /// Pointer to the class used for memory
/// allocation and deallocation
};
这个类实现了一个链接指针列表。如果我们的程序以这样的方式使用该类,即把变量 head 和 count 作为一个包来访问,那么它们应该一个接一个地放在类定义中。在这种情况下我们增加了它们实际在同一缓存行中的概率。
使用数据数组替换指针数组
当谈到类或结构的数组时,人们想到的第一个想法是使用指针而不是值。这种解决方案与数组相比有很多优点,包括运行时的多态性和在数组中未分配元素的情况下,对内存的使用更少,但会有一个性能缺陷。 使用指针访问该变量时,必然会涉及到高速缓存的缺失。 因此,为了快速访问数组,可以不使用指针而使用值。
因此,现在当把类的数组作为值时,我们将获得一些好处。每当我们访问数组中的一个元素时,缓存预取器就会获取更多与我们当前访问的元素接近的元素。 如果,我们访问的是数组中彼此相邻的元素,数据缓存被最大限度地利用了。
优化对类或结构数组的访问
如果我们以随机的方式访问数组中的元素,就会出现一些缓存丢失的情况。但是我们会有更多或者更少的丢失取决于我们在类中如何组织数据。例如:
假设我们有一个类my_class 并且该类的大小为 48btyes。阵列的第一个元素从偏移量 0 开始,第二个元素从偏移量 48 开始,第三个元素从偏移量 96 开始,第四个元素从偏移量 96 开始。如果我们的cache line是64bytes,那么意味着第一个类元素在第一个 cache line 中,第二个元素将被分别存在第一个和第二个cache line中,第三个元素也将被分别存在两个 cache line 中...
在对类的元素进行随机访问的情况下,将一个元素分割在两个高速缓存线之间,从数据缓存利用率的角度来说是不好的。缓存存储器需要两次访问主存储器才能读取一个元素。那么如何避免呢?如何使每个元素适合最小数量的cache line?下面是一些规则:
- 类的大小需要是cache line大小的倍数。
- 数组的起始地址需要是cache line大小的倍数。
要使类的大小是缓存行大小的倍数,我们可以手动的填充使其满足cache line 或者告诉编译器自动帮我们填充,在C++11中允许使用alignas(64) 来指定。当然 GCC/CLANG 编译器提供了 __attribute__((aligned (64))) 实现相同功能。更好的解决方案是让编译器和库来帮助我们;我们可以用 posix_memalign 去分配对齐的内存在堆中,或者使用alignas(64) 和 __attribute__((aligned (64))) 在栈或者全局内存中分配内存。下面是一个使用posix_memalign分配类数组的例子:
my_class* array_of_my_class;
posix_memalign((void**)array_of_my_class, 64, SIZE * sizeof(my_class));
for (size_t i = 0; i < SIZE; i++) {
::new (&array_of_my_class[i]) my_class(i);
}
语法看起来非常的复杂,其实很简单。我们声明了my_class 类型的指针,该指针用来保存类数组。接下来我们使用posix_memalign 去为数组分配内存。同时指定了对其参数为64。最后,在循环中,我们为数组中的每个元素调用构造函数。注意,我们使用的是::new操作符,这个操作符不做内存分配,而是它在作为参数提供的内存上执行构造函数(简单的说,就是执行 array_of_my_class[i] 构造函数,而不进行内存分配)。
有效地访问你的矩阵中的数据
如果你的程序需要处理矩阵,你需要了解矩阵是如何存储在内存中的。矩阵被定义为二维的,但是内存是一维的。C 和 C+ 编译器将矩阵逐行排列。这就意味着如果我们获取矩阵中的某个元素,和这个元素在相同行的一些元素也已经被加载到数据缓存中。
这看起来微不足道,但它会对性能产生深远的影响。考虑一下简单的矩阵乘法算法:
void multiply_matrices(int in_matrix1[][N], int in_matrix[][N], int result[][N])
{
int i, j, k;
for (i = 0; i < N; i++) {
for (j = 0; j < N; j++) {
result[i][j] = 0;
for (k = 0; k < N; k++) {
result[i][j] += in_matrix1[i][k] * in_matrix[k][j];
}
}
}
}
矩阵相乘就是对in_matrix1 的行,和对in_matrix2 的列做运算,按照这个计算规律结合上文的内容,我们可知in_matrix1 是符合缓存规律的,但是,in_matrix2 将会是缓冲的灾难。在in_matrix2 中每访问下一个元素都会导致 cache 丢失,因此上面的代码具有很大的性能缺陷。
那么如何解决上述问题?其实很简单。进行一种叫做循环互换的转换。 将j上的循环移到最里面的位置。这个解决方案的具体实现如下:
void multiply_matrices(int in_matrix1[][N], int in_matrix[][N], int result[][N])
{
int i, j, k;
for (i = 0; i < N; i++) {
for (j = 0; j < N; j++) {
result[i][j] = 0;
}
for (k = 0; k < N; k++) {
for (j = 0; j < N; j++) {
result[i][j] += in_matrix1[i][k] * in_matrix[k][j];
}
}
}
通过这种转换,逐行运行in_matrix,也要逐行运行result。这对性能有很大的影响。
在你的类和结构体中避免填充
关于数据对齐的一个小说明, 适用于所有原始数据类型,如果数据类型为4字节大小,其起始地址需要能被 4 整除。如果数据类型为8字节大小,其起始地址需要能被 8 整除。以此类推对于N字节大小的数据类型,它的起始地址应当能被 N 整除,我们说变量是正确对齐的,或是对齐的,此外都是未对齐。对齐要求通常是由硬件提出的,并由编译器尽可能地强制执行。
为了确保你的类和结构中的数据能正确对齐,C 和 C++ 编译器可以添加填充:这些是在类的成员之间添加的未使用的字节,以确保所有成员都正确对齐。请看下面的例子:
class my_class {
int my_int;
double my_double;
int my_second_int;
};
人们期望这个结构体的大小是sizeof(int) + sizeof(double) + sizeof(int) = 16 ,然而,double需要8字节对其。因此在my_int 之后,编译器添加了 4bytes 的填充,此时my_double 内存对齐了。因此,当前的结构体需要20bytes。
此外,为了使类的数据在数组中正确对齐,类采取了根据其最大成员大小来对齐。而且类的大小是其最大成员大小的整数倍。在上面的例子中,整型是 4 字节对齐,双精度浮点型是 8 字节对齐,因此我们的类应当 8 字节对齐。由于类的大小需要是其对齐方式的倍数,编译器在类的末尾增加了 4 字节的填充。因此,类的大小从原来的 20 字节增加到 24 字节。填充物是如何影响缓存效率的?比方说,我们的高速缓存存储器有一个 64 字节的 cache line。在我们的例子中,只有2.7个my_class 类可以填充到 cache line 中,而不是我们所期望的四个类实例。另外,填充字节被加载到高速缓存中,但是你的程序是不会用这些填充字节的。这保证了编译器不会插入任何填充物,程序将更好地使用数据缓存。下面对上面类进行了修改的类,其类成员的顺序略有修改,从而避免编译器填充。
class my_class {
double my_double;
int my_int;
int my_second_int;
};
这个类的大小现在是 16 字节,四个类实例符合一个 cache line 大小。
在linux中有个叫做 pahole工具可以查找你类的填充,它需要从源码构建。并且不支持 C++11。
尽可能的使用最小的类型
尽可能的使用字节数少的类型也是避免编译器填充的一种方法。有时short 可以满足需求的,我们却习惯性的用int 。或者说在你的类的定义中有几个bool变量,你用它来保持各种flag。你可以用chars或bool位域来代替使用bool。
class my_class {
public:
bool my_bool1:1;
bool my_bool2:1;
bool my_bool3:1;
bool my_bool4:1;
int my_int:1;
};
在上面的例子中,每个 bool 占了 1 bit。但是,编译器为了和 my_int 对齐会在 my_bool4 后面自动填充。这可以通过重新安排my_class成员的顺序来避免。
另外的例子:一个64字节的cache line可以存储8个整型或者4个长整型。 如果你有一个 1M 元素的数组,若该数组元素是整型那么将占 4MB,若为长整型就是 8MB。显而易见的是,加载 8MB 到缓冲中,比加载 4MB 慢。
但要注意!处理器在内部以原生字节数(例如:8字节对于现代64位计算机,或者在嵌入式系统的结构中,可能适用更小的字节数)为最佳工作方式。 使用较小的数据类型甚至可能降低速度。因此,你将需要测量以获得确定的性能差异。
尽可能避免堆分配
由于下面几个原因,堆的效率很低:
- 调用
malloc和free是很慢的。 - 对这些位置的访问是间接(通过指针)的,这种方式将导致更多的高速缓存不命中的情况。
另一方面,栈顶几乎总是在缓存中,分配和删除的速度超快。你可以用下面几个技巧来加速。如果,你的程序需要分配可变大小的数组,可以考虑在栈而不是堆上分配数组( GCC 支持但是有些编译器不支持)。如果,你的程序需要使用malloc分配大量的小内存块,可以考虑分配一个大的内存块,然后根据你的需要把它分成小的。如果,你的程序需要频繁的分配和释放同一类型的对象,那么我们可以考虑缓存内存块,而不是直接释放,如果我们重新需要时,可以很快的重新分配。
尽可能的重复使用缓冲中的数据
理想情况下,我们希望从内存中加载数据到缓存中,对其进行一些修改,然后再把它们返回到操作内存中。如果你需要两次获取相同的数据,你就没有最佳地使用缓存。
以查找一个数组中的最大元素和最小元素为例。
int * a = initialize_array(size);
int min = find_min(a, size);
int max = find_max(a, size);
我们在这里调用了两个函数,一个是找到最大值,一个是找到数组中的最小值。每个函数都有自己的循环,并在循环中遍历数组中的元素。
假设数组足够大,数组中的元素将被加载到缓存中两次。
解决办法很简单:在一个循环中完成对数组的所有工作。下面是更正后的版本。
int * a = initialize_array(size);
int min = a[0];
int max = a[0];
for (int i = 0; i < size; i++) {
min = std::min(a[i], min);
max = std::max(a[i], max);
}
这里我们只对数组进行一次迭代。数组数据只被加载到数据缓存中一次,这样可以更好地利用数据缓存。
尽量避免写内存
所有对内存的写入都要经过数据高速缓存。当进行写操作时,缓存将该 cache line 标记为 "dirty"。若一个 cache line 是 dirty 的,这就意味着他和内存中的数据不同,它的内容迟早会被写回内存中。这导致了速度的减慢。请看这两个算法:
void sort_fast(int* a, int len) {
for (int i = 0; i < len; i++) {
int min = a[i];
int min_index = i;
for (int j = i+1; j < len; j++) {
if (a[j] < min) {
min = a[j];
min_index = j;
}
}
std::swap(a[i], a[min_index]);
}
}
void sort_slow(int* a, int len) {
for (int i = 0; i < len; i++) {
for (int j = i+1; j < len; j++) {
if (a[j] < a[i]) {
std::swap(a[j], a[i]);
}
}
}
}
上面的代码显示了两个类似的数字排序的函数。两者的工作方式相同。找到最小的元素并把它放在 0 的位置,然后找到下一个最小的元素并把它放在 1 的位置,以此类推。
方法 sort_slow 寻找比 a[i] 小的数组元素,如果找到就立即交换。 每当发现一个比 a[i] 小的元素时,它就会继续交换元素。方法sort_fast 寻找数组中比a[i]小的元素,但它不做交换,而是将新的最小元素保存在临时变量min和min_index中(编译器为这些临时变量使用一个寄存器)。 当函数完成对数组的运行并找到最终最小的元素时,才会替换a[i]和a[min_index]的内容。 在我的系统上,函数sort_fast比sort_slow快 2 倍。
正确对齐你的数据
你的变量需要正确对齐。这样可以确保整个变量位于一个缓存行中,而不是被分割在两个缓存行中。如果你的系统不支持对错位变量的访问,获取数据会变得非常慢,因为你的操作系统可能会模拟对错位内存地址的访问。大多数时候,编译器会确保数据正确对齐,但不细心开发者可能会创造出内存访问错位的地方。这种情况经常发生在将指针从一种类型转换为另一种类型指针的时侯。错误示范:
unsigned char serialized_data[1024];
read_data(serialized_data);
int* header_pointer = (int*) (serialized_data + 3);
int header = *header_pointer;
在这个例子中,我们将 char 指针转换为 int 指针,从而使 header_pointer 错位。解除对header_pointer的引用会产生错位的内存访问。在某些架构上,程序会崩溃,在其他架构上,程序会变慢。正确示例:
unsigned char serialized_data[1024];
read_data(serialized_data);
int* header_pointer = (int*) (serialized_data + 3);
int header;
memcpy(&header, header_pointer, sizeof(int));
在这里,我们使用memcpy将输入数组中的值复制到 header 变量中。函数memcpy不需要适当的对齐,这段代码更好地利用了数据缓存,而且它是可移植的。
使用软件预取
如果你的算法不是一个一个地访问数据,而是以随机的方式在内存中跳跃,你可以使用软件预取来告诉处理器你将访问哪些数据,这样它就有时间在需要它们之前将它们加载到缓存中。例如,GCC 和 CLANG 编译器提供了__builtin_prefetch内置,允许软件预取。这里我们举一个二分搜索算法的例子:
int binarySearch(int *array, int number_of_elements, int key) {
int low = 0, high = number_of_elements-1, mid;
while(low <= high) {
mid = (low + high)/2;
#ifdef DO_PREFETCH
// low path
__builtin_prefetch (&array[(mid + 1 + high)/2], 0, 1);
// high path
__builtin_prefetch (&array[(low + mid - 1)/2], 0, 1);
#endif
if(array[mid] < key)
low = mid + 1;
else if(array[mid] == key)
return mid;
else if(array[mid] > key)
high = mid-1;
}
}
二分搜索算法不按顺序运行数组,硬件缓存预置器面临大量的缓存缺失。在上面的二分搜索算法中,我们在进行数据查找之前就预取了内存中 high 的新值和 low 的新值。而当我们真正需要这些数据时,它已经存在于缓存中了。
这个特定算法的缺点是,我们获取两个值。而其中一个值我们将永远不会被使用。这可能会对性能产生影响,因为一些 cache line 现在需要离开缓存,以便为未使用的值腾出位置。如果另一个程序在另一个使用相同缓存的核心上运行,可能会导致两个程序的性能下降。
实验
让我们看看这些技巧对我们的实际问题有何帮助。在测试中,我们使用一个普通的通用系统AMD A8-4500M CPU,有四个核心,每个核心有16KB的L1数据缓存,每个核心有2MB的L2数据缓存(两个核心共享2MB的L2数据缓存)。这个系统有12GB的内存。
矩阵乘法
这里有一篇由 Ulrich Drepper 写的关于缓存优化的文章,非常好,但也很冗长。他从简单的矩阵乘法算法开始,不断完善,直到得到一个优化的版本,速度几乎快了十倍。在他的实验中,他使用了一个1000×1000的双精度浮点矩阵。 他做的第一个优化是在乘法前对矩阵进行转置,仅此一项就带来了76.6%的性能提升!
带软件预取的二分搜索算法
我们实现了一个使用前一章中的软件预取的二进制搜索算法,我们用它来测试当程序员明确使用预取时,内存缓存子系统是如何工作的。我们使用的程序源码放在了 github 中。只需要输入make binary_search_runtimes 和 make binary_search_cache_misses 就可分别生成带预取和不带预取的程序。
我们生成了一个排序的随机整数数组,长度为 10K, 100K, 1M, 10M 和 100M。我们用这些数组来进行二分搜索。我们称其为 input_array 。我们使用几种不同的方法来生成 index_array 的索引。并使用随机的方法来生成 index_array 的元素, 但我们也使用了一种基于非随机步长的方法。 如果步长是 N,index_array 的第一个元素是 0,第二是 N,第三是 2N 等等,直到我们到达数组的末端,然后绕过。
因此,代码实现如下:
for (int i = 0; i < len; i++) {
binarySearch(inputArray, len, inputArray[indexArray[i]]);
}
我们对随机 index_array 和步长为 1、100 和 10K 的 index_array 都进行了测试。 我们将 index_array 的大小固定为 10M ,这意味着我们正在进行 10M 的搜索。 对于随机访问的 index_array,下面是结果。
| 工作集 | 关闭Prefetching | 开启Prefetching | 速度差异 |
|---|---|---|---|
| 10K | 1673ms | 1777ms | -6.2% |
| 100K | 2478ms | 2426ms | +2.1% |
| 1M | 4519ms | 3996ms | +11.6% |
| 10M | 8804ms | 7096ms | +19.4% |
| 100M | 14970ms | 11685ms | +21.9% |
上表表示了在随机访问的情况下二分搜索的运行时间和工作集大小的关系。
对于随机访问,软件预取对最小的10K数据集来说是负优化。随着工作集的增加,带软预取的算法也会变得比普通算法快。对于大的工作集来说,速度上的差异大约是20%,而且即使工作集的大小进一步增加,它也会保持这种状态。如果我们不是在访问随机元素,而是在以恒定的步长访问元素,会发生什么?由于这是一个合成测试,我们正在寻找一个我们事先知道位置的元素。例如:如果步长是 100,我们知道第一个元素的位置是 0,我们正在寻找 input_array[0] 这个值。在下一次迭代中,我们要寻找一个元素 input_array[100] 等等。 在这种情况下,缓存是如何表现的?下面是结果。
| 工作集 | 关闭Prefetching | 开启Prefetching | 速度差异 |
|---|---|---|---|
| 10K | 977ms | 1168ms | -19.5% |
| 100K | 1122ms | 1380ms | -23.0% |
| 1M | 1367ms | 1623ms | -18.7% |
| 10M | 1610ms | 1892ms | -17.5% |
| 100M | 1813ms | 2171ms | -19.7% |
上表是 步长=1 的情况下二分搜索的运行时间和工作集大小的关系。
| 工作集 | 关闭Prefetching | 开启Prefetching | 速度差异 |
|---|---|---|---|
| 10K | 1112ms | 1418ms | -27.5% |
| 100K | 1766ms | 1942ms | -9.7% |
| 1M | 3018ms | 2792ms | +7.5% |
| 10M | 3236ms | 3019ms | +6.7% |
| 100M | 3356ms | 3182ms | +5.2% |
上表是 步长=100 的情况下二分搜索的运行时间和工作集大小的关系。
| 工作集 | 关闭Prefetching | 开启Prefetching | 速度差异 |
|---|---|---|---|
| 10K | 760ms | 984ms | -29.5% |
| 100K | 1049ms | 1508ms | -43.8% |
| 1M | 2739ms | 2640ms | +3.6% |
| 10M | 4402ms | 7490ms | -70.1% |
| 100M | 10395ms | 8251ms | -20.6% |
上表是 步长=10K 的情况下二分搜索的运行时间和工作集大小的关系。
对于stride=1,普通算法每次都能击败软件预取算法。不过这并不奇怪,因为前一次迭代的所有数据都已经在缓存中了。
对于stride=100,正如预期的那样,对于小的工作集,一般的算法胜过软件预取算法。但是随着工作集的增加,软件预取算法平均快6%。为什么在这种情况下,与完全随机的情况下的20%相比,平均快6%?如果我们的工作集是10M,平均来说,该算法在20步左右完成。在这20步中,有14步的数据已经在之前搜索的缓存中了。因此,只有在最后的6步中,软件预取才有意义。
对于stride = 10K,我们看到一个非常奇怪的行为,即一般算法比软件预取算法快。为什么呢?答案是,在步长为10K时对于输入的10M的工作集,这相当于将其减少到只有10K的工作集。因此,即使是最大的工作集大小(10M),通用算法也更快,与随机索引和工作集10K的通用算法的百分比几乎相同。
缓存性能如何?预取对缓存性能有什么样的影响。让我们比较一下有预取和无预取的pref指令的结果。
| Parameter | 关闭Prefetching | 开启Prefetching | 差异 |
|---|---|---|---|
| 缓存引用 | 409M | 649M | +58.7% |
| 缓存丢失 | 155M | 254M | +63.9% |
| Cycles | 31481M | 25648M | -18.5% |
| 指令数 | 6659M | 10647M | +59.9% |
两个版本的二分搜索的缓存性能、周期和指令数据。结果是有趣的。与普通版本相比,软件预取版本有更多的缓存引用,更多的缓存丢失和更多的指令执行。这意味着,软件预取版本实际上做了更多的工作。但它还是更快,因为它在较少的周期内做了更多的工作。现代处理器每个周期可以执行一条以上的指令,但如果处理器需要等待从主存储器中获取数据,这个数字就会下降。如果我们计算每个周期的指令数,软件预取版本为0.42,普通版本为0.21。这是一个巨大的差异。
缓存友好的链表
第二个实验是一个有利于缓存的链表(这些列表也被称为 unrolled 链表)。普通的链表对缓存非常不友好,在这样的结构中迭代会导致很多缓存丢失。我们怎样才能做得更好呢?
常规的链接列表通常由链接列表节点组成,每个节点持有一个值和指向下一个节点的指针。在我们的实现中,链表节点可以持有一个以上的值,值的数量被指定为 linked_list 类的一个模板参数。我们测试了可以容纳 1、2、4和 8 个值的链接列表节点,节点中值的数量越大,缓存失误就越少。我们用来测试的程序的源代码可以在 github 上找到。要运行它,只需执行 make linked_list_runtimes 和 make linked_list_cache_misses 即可。
我们唯一感兴趣的是测试在链表中的进行插入、删除等。我们的实现也比简单的链表快,但大部分的性能改进来自于更少的内存分配,而不是更好地使用数据缓存。下面是一个单一列表节点的源代码。
class linked_list_node {
public:
char used_elems[count];
linked_list_node* next;
char values[count * sizeof(Type)];
...
};
常量 count 保存单个列表节点中的值的数量,模板常量 Type 是我们在节点中保存的类型。由于一个节点有不止一个值,我们在数组 used_elems 中标记哪些值是实际使用的。注意,我们使用字符来保存使用的值,而不是bool。在我的机器上,bool需要四个字节,而char需要一个字节。这个选择确实提高了列表的性能,因为更多来自节点的其他数据将被预取到缓存中。
现在让我们开始测量。下面的图表测量了迭代链表所需的时间,这取决于节点中的值的数量(1、2、4和8)和链表的值的类型大小。
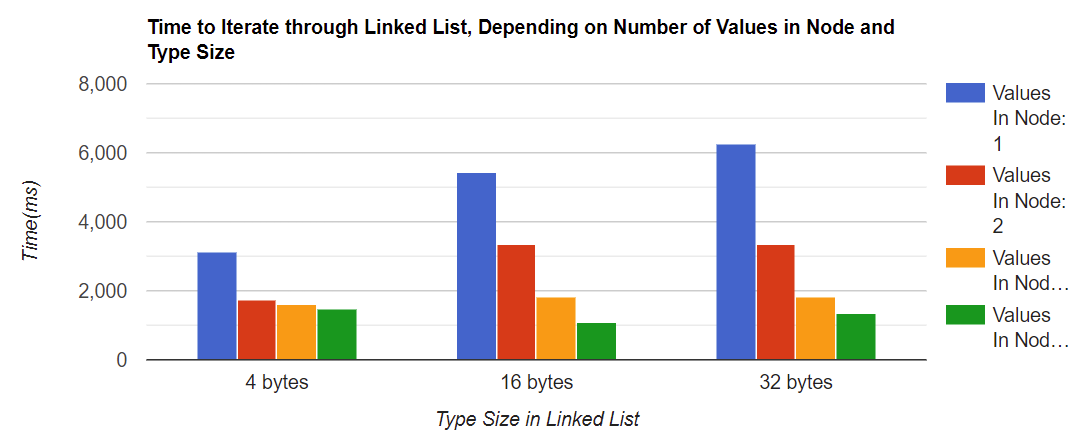
结果看起来非常好! 对于最小的类型大小,遍历一个节点中有两个值的链表比遍历一个值的链表要少花43%的时间,而且这个数字对于所有类型大小都大致相同。还要注意的是,列表中的类型大小越大,在单个链表节点中拥有更多的值就越有意义。对于4字节的类型大小,有两个值的节点和有四个值的节点之间的差异很小,但对于32字节的类型大小,这种差异是明显的。
缓存性能如何?在我们的测试中,内存读取次数和数据缓存失误率是多少?首先让我们测量一下我们的程序有多少次内存读取。
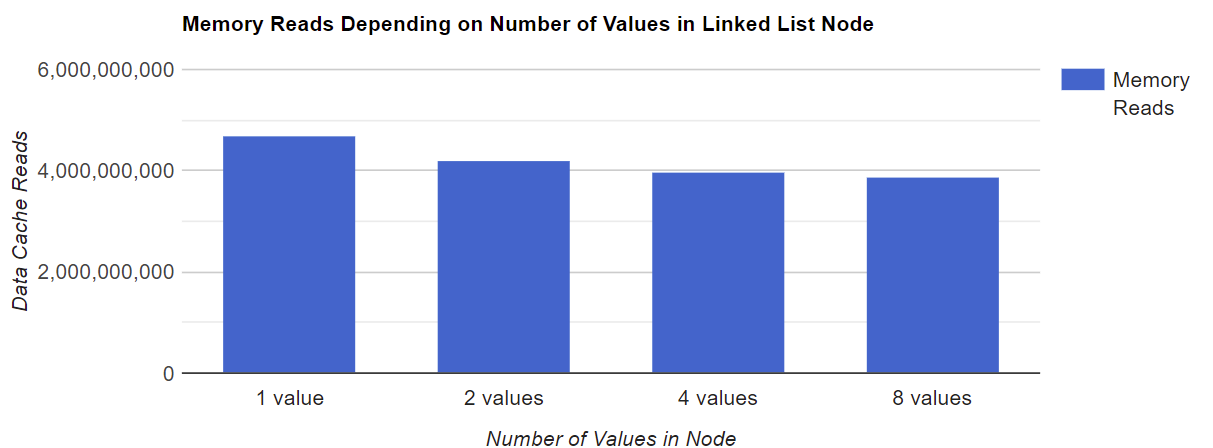
正如你所看到的,单个节点中存储的数值越多,读取的内存总量就越少。这是可以预期的,因为涉及的指针算术较少。请注意,在我们的例子中,内存读取的数量并不取决于类型大小。
缓存缺失情况如何?我们使用了 cachegrind 工具来测量高速缓存失误率。它可以提供关于每个函数或每行的缓存缺失的信息。下面是结果。

一般的趋势是:如果一个链接列表中的值越多,缓存缺失的次数就越少。对于最小的类型,节点中8个值的缓存丢失率为3%,而节点中1个值的缓存丢失率为10%。对于较大的类型也观察到类似的比率。另一个趋势是:在一个链接列表节点中,类型大小越大,缓存缺失率就越大。对于4字节的类型大小,最坏的情况下缓存丢失率为10%,最好的情况下为3%。对于32字节的类型大小,最坏的情况下缓存缺失率为20%,最好的情况下为13.6%。没有什么意外。当我们访问节点中的第一个值时,缓存预置器会在周围的内存地址中加载值,所以当我们以后需要它们时,它们已经在缓存中了。如果类型越大,预置器加载有用数据的机会就越少,所以这也是造成额外的缓冲区失误的原因。
总结
那么结论是什么呢?无论是在我们的实验中还是在一般情况下,关于数据缓存的优化肯定有一些有趣的说法。
关于实验的总结
那么结论是什么呢?我们先谈谈我们的实验:这三个实验都表明,更好地利用数据缓存,会取得性能上的提升。与非优化版本相比,优化后的矩阵乘法有很好的性能提升,但是除了矩阵之外,我们很少能在数据结构上做一个简单的操作来使我们的结构更适合缓存。而在我的专业经验中,我也很少看到矩阵作为数据结构使用。
第二个实验是关于软件预取的。我们确实看到了软件预取在二分搜索上的性能提升,但性能提升只与不合适数据缓存的工作集有关。需要注意,软件预取是有代价的:我们的系统执行了更多的指令,并将更多的数据加载到缓存中,这在某些情况下可能会导致其他方面的性能下降。软件预取的好处是,它很容易实现,可以用来加快各种结构的迭代速度:链表、树、堆等。然而,需要仔细测量以确保性能的提高是值得的。
我们的第三个实验是关于缓存友好的链表。我们再次看到速度有了很大的提高。改进来自几个方面:更少的内存分配,更小的数据缓冲区失误率和更少的指针运算指令。唯一的缺点是实现更复杂,而且内存消耗增加,因为可能会出现单个节点没有被最佳填充的情况。但一般来说,我认为这些缺点是值得努力的。
对于数据缓存优化的总结
正如我们的实验所显示的,以及我之前的经验,优化确实带来了性能的提升,而且有许多应用都需要这样做。性能的提高取决于许多因素,范围可以从百分之几到百分之百甚至更多。
然而,这里提出的一些建议会使你的程序更难理解,更难调试。而开发人员一直认为要避免的正是这一点,原因很充分。为了最大限度地从这些优化中获益,你需要仔细地对你的程序进行剖析,找到瓶颈,并专注于加速这些瓶颈,而不是在你的代码中到处应用这些技巧。首先,应当保持你的接口干净,避免模块间的依赖,然后用更快的代码替换你的慢代码就很简单了,你可以在不牺牲可维护性的情况下享受性能的提升。
参考
Ulrich Drepper “What every programmer should know about memory”


 浙公网安备 33010602011771号
浙公网安备 33010602011771号