杂题集2

第 $21 \sim 40$ 道杂题。

（完结于 $2025.3.19$）

独钓寒江雪

给定一棵无根树，求其中本质不同的独立集的个数。

$1 \le n \le 5 \times 10^5$。

树的同构。

首先考虑有根树该怎么做。

显然想到 DP，$dp_{u,0/1}$ 代表以 $u$ 为根的子树中选/不选 $u$ 的方案数。并不能直接进行转移，因为如果存在一个节点两个儿子 $x,y$ 满足以 $x$ 为根的子树和以 $y$ 为根的子树同构就会算重。

经典盒子与球，把儿子当作相同的球，所有方案数当作不同的盒子，由于盒子可以为空，所以提前在每个盒子放上一颗小球，然后插板法就行了。

考虑回无根树，经典套路以重心为根，但可能存在两个中心。特判一下就行。

[CF1844G] Tree Weights

给你一棵节点编号为 $1\sim n \ (2≤n≤10^5)$ 的无根树，每条边有未知的正整数边权。

现在对于所有的 $1 \le i \lt n$，给出点 $i$ 到点 $i+1$ 的距离 $d_i \ (1≤d_i≤10^{12}) $，请你还原出任意一组合法的边权或输出 −1 报告无解。

让人眼前一亮的一道题。

与树上路径有关，容易想到将 $d_i$ 与 lca 联系在一起。

以 $1$ 为根，令 $dep_i$ 表示 $i$ 号节点的深度。容易得到 $d_i=dep_i+dep_{i+1}-2 \times dep_{\text{lca}(i,i+1)}$，变式得到 $dep_{i+1}=d_i-dep_i+2 \times dep_{\text{lca}(i,i+1)}$。

$dep_1=0$，发现主要难以处理的地方在 $dep_{\text{lca}(i,i+1)}$。注意到这一项的系数为 $2$，也就是说我们可以先将其舍弃然后考虑所有 $dep_i$ 的奇偶性。相当于求出了所有 $dep_i \ \text{mod}\ 2$ 的值。

紧接着我们惊奇地发现由于这个 $2$ 的系数，所有 $dep_i \ \text{mod}\ 4$ 的值只与 $dep_{\text{lca}(i,i+1)}\ \text{mod}\ 2$ 有关。

因此直接递推下去到 $2^{60}$ 就行了。

当然，以上结论都是在有解的情况下才成立。无解的情况结尾的时候特判一下有没有矛盾就行了。

[CF1849E] Max to the Right of Min

现有一长度为 $n(n≤10^6)$ 的排列，求有多少子区间 $[l,r]$ 满足区间最大值出现在区间最小值的右侧。

I love Edu。

扫描线

老样子扫描线，枚举 $r$。

发现只有在 $a_r$ 是区间最大值或区间最小值是才有可能对结果产生影响。

令 $mi_i$ 表示 $i$ 左边第一个比它小的，$ma_i$ 表示 $i$ 左边第一个比它大的，线段树上 $i$ 号节点为 $0/1$ 表示 $[i,r]$ 是否合法。

每次遇到一个新的 $r$ 就 $0 \to [mi_{r}+1,r-1],1\to [ma_r+1,r-1]$。

区间覆盖就行。

启发式分裂

这个是正题。

通过单调栈可以求出 $i$ 作为最小值的所有区间 $l\in[l_i,i],r\in[i,r_i]$。

其实可以发现能通过暴力枚举 $l$ 或 $r$ 来计算当前的贡献。

关键的关键在于 $\sum\min(i-l_i+1,r_i-i+1)$ 是 $n \log n$ 级别的。

为什么呢？你可以考虑将 $i$ 从小到大放入，每一次就相当于在原序列中加上了一堵墙，之后的区间都不能越过这堵墙。

这就可以使得覆盖任意一个点的区间的长度都至多是上一次覆盖这个点的区间长度的一半，因此每个点至多被覆盖 $\log n$ 次。

这个东西好像叫启发式分裂。

[NOI2025省选模拟赛16] 镜子

$n \times n$ 的方格图上有 $k$ 个障碍物，从 $(1,1)$ 出发，初始方向向下，令 $f(i,j)$ 表示到达 $(i,j)$ 所需的最少转向次数，若无法到达 $(i,j)$ 则 $f(i,j)=0$，求 $\sum f(i,j)^2$。

$1\le n,k \le 10^5$。

发现每一行/列都可以以障碍为分解划分为若干个连续的段，我们尝试把这些段缩成一个点，行列之间有交点的段之间有一条长度为 $1$ 的边。此时从 $(1,1)$ 所在的竖直的一段开始 bfs 即可。

这里我们维护两棵树套树先加入所有段，然后 bfs 是动态查询+删除即可做到 $\text{O}(n \log^2n)$ 的复杂度。

接下来的问题是如何计算最终的平方的结果，一个点的贡献有可能来源于所在的横段或竖段，当然可以使用数据结构维护，不过就显得很麻烦了，这里有一个非常有意思的方法。

发现横段和竖段的差值一定为 $1$，因为横段一定是奇数，竖段一定是偶数。所以若正确答案为 $d$，那么横段竖段的值就一定是 $d$ 与 $d + 1$。考虑拆贡献，令 $v_d=\frac{d(d-1)}{2}$，发现我们要求的 $d^2=v_d+v_{d+1}$，因此直接把每一段的贡献相加就行了。

[CF1739E] Cleaning Robot

给定一个由 $2×n$ 个格子组成的走廊。有一些格子是脏的。从 $(1,1)$ 释放一个机器人。每次机器人会选定最近的一个脏格子，移动到那个格子上并清理该格子，直至全部脏格子被清理。

然而机器人如果在选定下一个清理的脏格子时，有两个或更多脏格子离它最近，那么机器人会崩溃。

可以在机器人之前进行人工清理，输出至多保留多少脏格子。

好题......

显然机器人不会往回走，可以 dp。

$dp_{i,j}$ 表示从第 $i$ 列第 $j$ 行出发只管 $i \sim n$ 列所能留下的最多脏格子数。

分讨。

若 $a_{i,j \oplus 1}=0$：直接 $dp_{i,j}=dp_{i+1,j}$。
否则若 $a_{i+1,j}=0$，此时如果将 $i$ 列 $j \oplus 1$ 行清理了就可以直接从 $i+1$ 列 $j$ 行走过来，或者从 $i+1$ 列 $j \oplus 1$ 行直接走，$dp_{i,j}=\min(dp_{i+1,j}+1,dp_{i+1,j \oplus1})$。
否则若 $a_{i+1,j\oplus 1}=0$，此时无论如何都要删去 $(i,j\oplus1)$ 或 $(i+1,j)$ 中的一个，所以直接 $dp_{i,j}=\min(dp_{i+2,0},dp_{i+2,1})+1$。
否则 $dp_{i,j}=\min(dp_{i+2,j}+2,dp_{i+2,j\oplus1}+1)$，手玩一下就行了，懒得讲了。

[CF1948G] MST with Matching

给定一个 $n$ 个点的无向连通图，$i, j$ 之间的边权为 $w_{i, j}$，再给定一个常数 $c$。

你需要找到这个图的一个生成树，使得这个生成树的权值最小。定义一个生成树的权值为以下两者的和：

生成树中所有边权的和；
生成树上最大匹配的大小乘 $c$。

$n \le 20$。

有点意思。

最大匹配等于最小点覆盖，所以直接暴力枚举点覆盖，然后将属于覆盖集的点的所有相邻的边抽出来跑全图的最小生成树即可。

[2022 集训队互测]Astral Birth

给定一个长度为 $N(1\le N \le 5\times10^5)$ 的 $01$ 序列。对于每个 $k \in [1,n]$，求出将原序列分任意为 $k$ 段后重新排列所能得到的 最长不降子序列。

非常好的一道题目。

这里有一个非常巧妙的转换：

在原问题中序列上分出来的 $k$ 段只会有一段的贡献可以是这一段的最长不降子序列，即 $01$ 交界处的那一段。剩余的要么是只有 $0$ 产生贡献，要么是只有 $1$。这时候发现，最长不降子序列作为贡献的那一段同样可以拆成一段 $0$ 贡献和一段 $1$ 贡献。

所以原问题就可以变成把序列拆成 $k+1$ 段，每一段中取 $0/1$ 的个数作为贡献的最大总贡献。

显然连续的 $01$ 段是一定会绑在一块的，所以就可以缩在一起。

此时原序列就由 $01$ 交替的块组成。

再次转化，每一块只有 $0,1$ 中的一个才能产生贡献，等价于删掉另一些。

题目就可以变为删掉一些段，求把剩下的相邻的同颜色段缩在一起后剩下 $k$ 段的最大长度。

很显然将相邻的块同时删去一定不会更优，毕竟只删一个另一个就一定可以缩掉。

由于不会删掉相邻的块，没删一个块就一定会减少两个块（缩相同颜色块后），边界只能减少一个，不过只需要最开始 $2 \times 2$ 枚举一下边界的情况就行了。

反悔贪心。

先将所有点都放入小根堆中，每次弹出的点就代表要删除。

由于序列中有删除块的操作，很容易想到使用链表来维护。

假如当前删掉了 $u$ 点，$pr_u$ 和 $ne_u$ 就合并到了一起，为了方便，我们把它作为新的 $u$，然后将 $pr_u$ 和 $ne_u$ 删去。

过后还有可能继续删去 $u$ 点，此时一开始被删去的 $u$ 点的权值就会被重新用到，而 $pr_u$ 和 $ne_u$ 就没了。

考虑设计一个新的权值满足撤销的操作。

每次让 $w_u=w_{pr_u}+w_{ne_u}-w_u$。容易发现这样每次直接减去 $w_u$ 就是满足条件的了。

举个例子：最初 $-w_u$，后来 $-(w_{u-1}+w_{u+1}-w_u)$，抵消，变为 $-(w_{u-1}+w_{u+1})$，删去 $u$ 的操作就被成功撤销了。

一直操作到被缩到只有 $2$ 个块就行，再删就不符合减去 $2$ 个颜色块条件了。因此 $ans_1$ 需要特殊处理一下。

细节有点多。

[NOI2019] 序列

给定两个长度为 $n$ 的正整数序列 $\{a_i\}$ 与 $\{b_i\}$，序列的下标为 $1, 2, \cdots , n$。现在你需要分别对两个序列各指定恰好 $K$ 个下标，要求至少有 $L$ 个下标在两个序列中都被指定，使得这 $2K$ 个下标在序列中对应的元素的总和最大。

$1\le n \le 2\times10^5$。

一眼盯真可以用费用流，图大概是长这样。

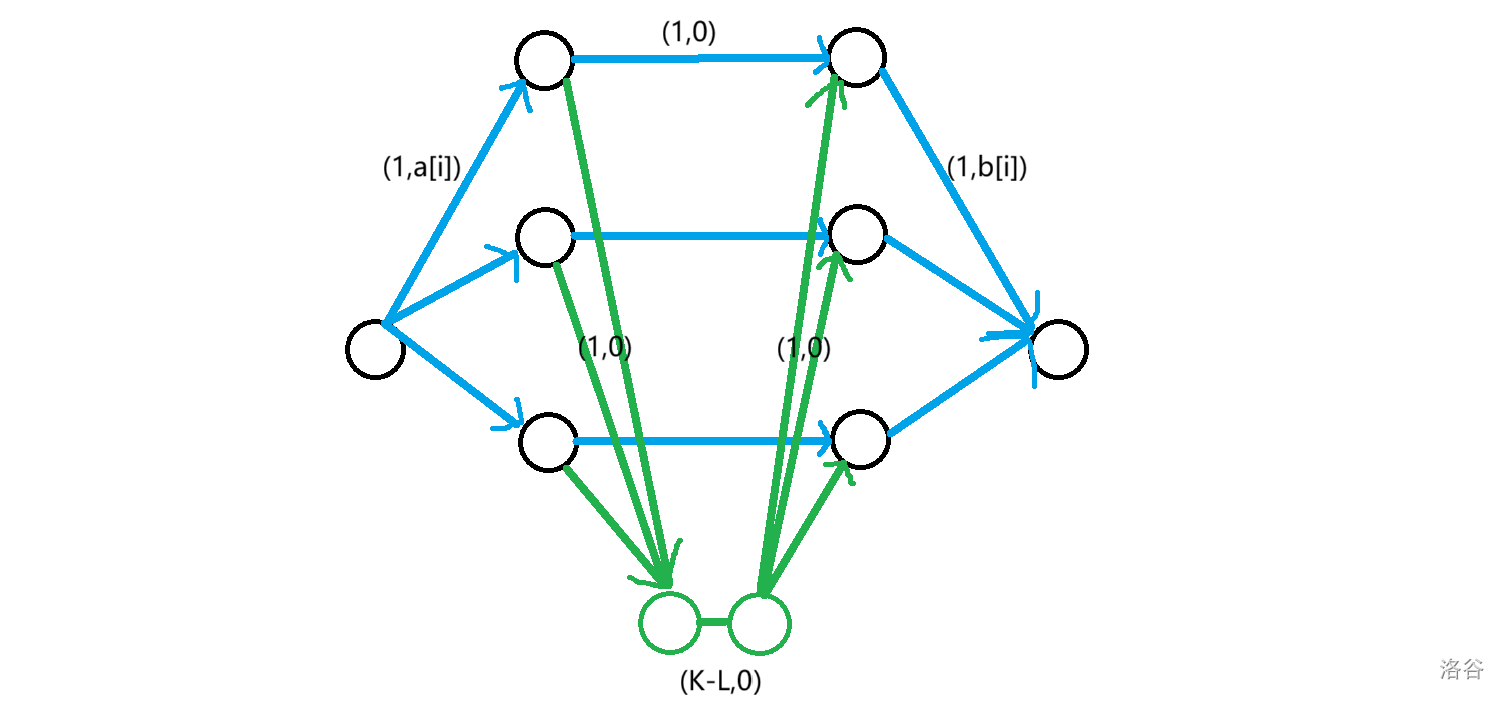
下方两个绿色的点代表下标不同的位置，所以容量为 $K-L$。

当然复杂度显然过不了，考虑模拟费用流。

每次照样贪心的选择权值最大的一条增广路，只是这里要注意下方绿色点的容量。

令 $a_i,b_i$ 都没选过的 $a_i$ 组成的集合为 $A$，只有 $a_i$ 没选过的为 $A^{’}$，$B$ 与 $B^{'}$ 同理。

$a_i,b_i$ 都没选过的直接由 $a_i,b_i$ 组成一组的构成集合 $C$。

发现一共只有 $5$ 中选择的情况：

$A,B$，此时由于两个点都没有选过，绿边的流量要加 $1$。
$A^{'},B$，另此时两个数分别为 $i,j$，$b_i$ 原先连的 $k$，那么此时可以把 $b_i$ 与 $k$ 断开，连接 $a_i,b_i$ 和 $j,k$，绿色流量不变。
$A,B^{'}$，同上。
$A^{'},B^{'}$ 差不多的思想，此时绿色流量会减 $1$。
$C$，此时绿色流量不变。

这样做的话维护 $5$ 个可删堆就行了。

[CF1097G] Vladislav and a Great Legend

给你一棵有$n$个节点的树$T$，$n$个节点编号为$1$到$n$。

对于$T$中每个非空的顶点的集合$X$，令$f(X)$为包含$X$中每个节点的最小连通子树的最小边数。求：

\[\sum_{X\subseteq\{1,2,\dots,n\},X\neq\varnothing}(f(X))^k \]

$2\leq n\leq 10^5,1\leq k\leq 200$。

DP 好题啊。

$(f(X))^k$ 不方便直接算，考虑拆开：

\[n^m=\sum_{i=0}^m\binom{n}{i} \times i!\times S(m,i) \]

其中 $S(m,i)$ 是第二类斯特林数。

因此可以推出：

\[\sum_{X}(f(X))^k=\sum_{i=0}^ki!\times S(k,i)\sum_X\binom{f(X)}{i} \]

然后就是主要考虑怎么求：$\binom{f(X)}{i}$。这玩意其实就相当于在 $X$ 所构成的虚树中选 $i$ 条边进行染色。

考虑树型dp。

令 $dp_{i,j}$ 表示在以 $i$ 为根的非空虚树中染色 $j$ 条边的方案数。

依次将 $dp_{son_u}$ 加入 $dp_u$。每次 $dp_u$ 和 $dp_{son_u}$ 所产生的 lca 为 $u$ 的方案数都计入贡献。

复杂度怎么证呢？

$son_u$ 并如 $u$ 的复杂度为 $\text{O}(\min(siz_u,k)\times \min(siz_{son_u},k))$。

可以将其想象为 $u$ 子树的 dfs 序的后 $k$ 位与 $son_u$ 子树 dfs 序的前 $k$ 位进行合并。

因此每个点只有可能与以其 dfs 差值小于 $2k$ 的点合并，复杂度为 $\text{O}(nk)$。

[CF573D] Bear and Cavalry

有 $n$ 个人和 $n$ 匹马，第 $i$ 个人对应第 $i$ 匹马。第 $i$ 个人能力值 $w_i$，第 $i$ 匹马能力值 $h_i$，第 $i$ 个人骑第 $j$ 匹马的总能力值为 $w_i\times h_j$，整个军队的总能力值为 $\sum w_i\times h_j$（一个人只能骑一匹马，一匹马只能被一个人骑）。有一个要求：每个人都不能骑自己对应的马。让你制定骑马方案，使得整个军队的总能力值最大。

现在有 $q$ 个操作，每次给出 $a,b$，交换 $a$ 和 $b$ 对应的马。每次操作后你都需要输出最大的总能力值。

$2 \le n \le 30000,1\le q \le 10000$。

比较有意思的一道题。

想一想如果没有不能骑对应的马该怎么做？

显然是排序一遍直接乘。

现在考虑有需要对应的情况，我们依然从大到小排序后做（这里懒得讲了，直接引用一张网上找到的题解的图）

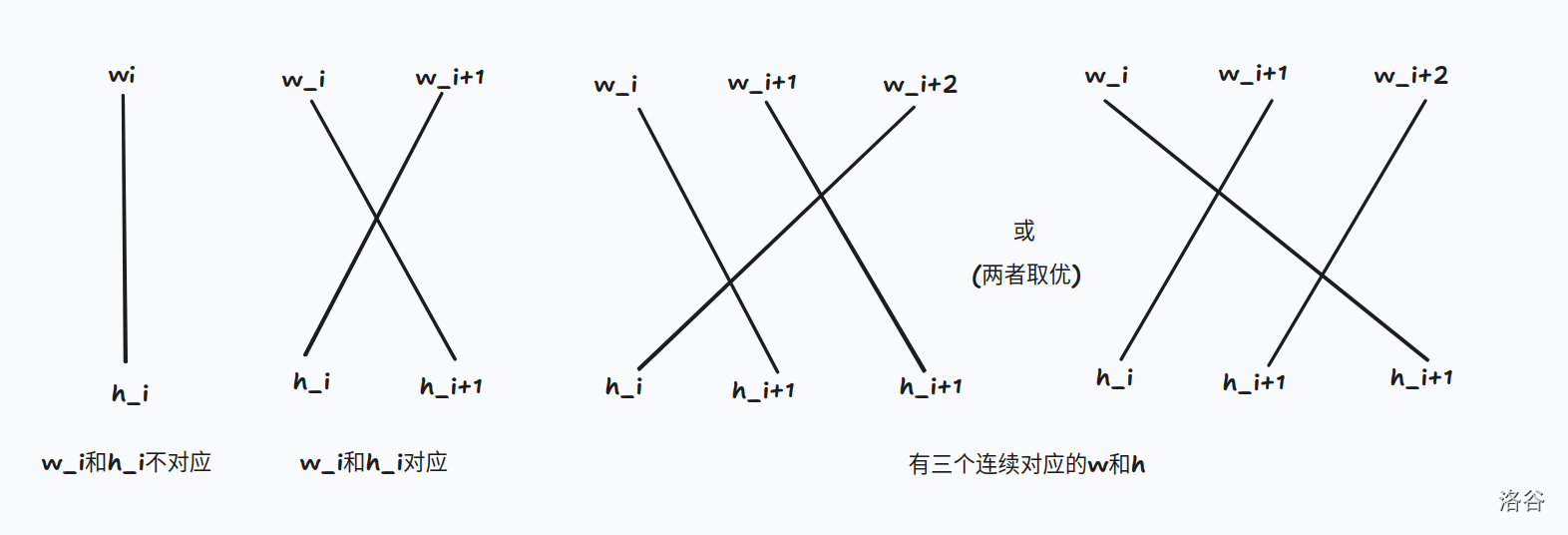
考虑如果有 $4$ 个连续的，其实直接当作两个两个的就行，依次可以发现每一个 $\ge 4$ 的都可以拆成 $2/3$，并且肯定是最优的。

（事实上这篇题解讲漏了一些，比如理论上应该在 $2/3$ 中取 $\max$，因为可能会存在对应+不对应+对应的情况）

然后直接矩阵中维护 $dp_i,dp_{i-1},dp_{i-2}$ 就行了，剩下有一点点细节，但是相对就十分简单了。

（吐槽：这玩意数据范围那么小，$nq$ 暴力都能过）

[CF1039D] You Are Given a Tree

有一棵 $n$ 个节点的树。

对于 $k \in [1,n]$，求出图中至多能有多少条点数为 $k$ 的互不相交的链。

$1\le n \le 10^5$。

根号分治。

暴力树型 dp 求出 $k\in[1,\sqrt n]$ 的值。具体方法就是每个点的最深和次深的路径合并起来如果满足条件就将答案加一，否则上传。

然后发现 $k\in[\sqrt n+1,n]$ 的情况中 $ans\in[0,\sqrt n]$，并且由于答案显然具有单调性，直接二分。

复杂度为 $n\sqrt n \log n$。

卡常：暴力的范围可以取 $2 \sqrt n$，节点按深度排序之后直接将递归改为递推，用链式前向星。

[AGC022E] Median Replace

有个长度为 $N$（$N$ 为奇数）的 $01$ 串 $s$，其中有若干位置是 ?。
一次操作可将 $3$ 个连续的字符替换成这三个数的中位数。
求有多少将 ? 替换成 $0$ 或 $1$ 的方案使得进行 $\frac{N−1}{2}$ 次操作后的字符串可以是 $1$。

$1\le N \le 3 \times 10^5$。

考虑从前往后枚举时的策略：

若此时前一个数是 $0$，若放入了一个 $1$，不论接下来再放什么，最优的方法都是这两个同归于尽。如果放入了一个 $0$，就不用管，当连续的 $0$ 达到 $3$ 个时，直接删成一个。
若此时前一个数就是 $1$，当此时放入了一个 $0$，就直接放，然后之后就按前一个数是 $0$ 的情况考虑了。档次是放入了一个 $1$，先留着，若 $1$ 的连续的个数达到了三个及以上，就一定能保证正确。

综上，定义 $dp_{i,0\sim2,0\sim3}$ 表示枚举到了第 $i$ 位，此时剩下的 $0$ 的个数与 $1$ 的个数，（$1$ 为 $3$ 是代表大于等于 $3$ 个），根据之前分析的结果，$1$ 不可能在 $0$ 的下方。

直接 dp 就行了。

[CF1540C2] Converging Array (Hard Version)

长度为 $n$ 的序列 $c$，与长度为 $n-1$ 的序列 $b$。

同时有一个序列 $a$，满足 $\forall i,a_i\in[0,c_i]$。

进行无穷次如下操作直到序列收敛。

选择一个 $i$，$\min\left(a_i, \frac{a_i+a_{i+1}-b_i}{2}\right) \to a_i,\max\left(a_{i+1}, \frac{a_i+a_{i+1}+b_i}{2}\right) \to a_{i+1}$。

进行 $q(1\le q \le 10^5)$ 次询问，每次给定一个 $x$，求满足收敛后 $a_1 \le x$ 的所有 $a$ 序列个数，对 $10^9+7$ 取模。

$1\le n,c_i \le 100$。

容易发现每一次操作的本质就是在 $a_{i+1}-a_i \lt b_i$ 的情况下从 $a_i$ 匀某个值到 $a_{i+1}$ 使得 $a_{i+1}-a_i = b_i$。

直接从正面硬想其实非常的困难，考虑从最终的 $a$ 序列出发。

首先一定是满足 $\forall i \in[1,n-1],a_{i+1}-a_i\ge b_i$，其中 $a_{i+1}-a_i\gt b_i$ 一定是从最开始就一直满足这个条件，那么这个 $i$ 相当与就把序列分割了，使得前后序列没有任何关系。

此时，令第一个出现分割的位置在 $p$。

令 $f$ 序列位收敛后的序列，则有：

\[\begin{cases}f_2-f_1=b_1\\f_3-f_2=b_2\\\dots\\f_p-f_{p-1}=b_{p-1}\\\sum_{i=1}^pf_i=\sum_{i=1}^pa_i\end{cases} \]

可以推出：

\[f_1=\frac{\sum_{i=1}^pa_i-\sum_{i=1}^{p-1}(p-i)b_i}{p} \]

令 $sa_i=\sum_{j=1}^ia_j,sb_i=\sum_{j=1}^{i-1}(i-j)b_j$，得到 $f_1=\frac{sa_p-sb_p}{p}$。

但是现在的问题是我们并不知道 $p$ 在哪里，但是我们可以发现当 $p$ 是第一个分割点时 $f_1$ 一定时最小的，因为如果前面还有分割点的话跨度变大只能减小初值。

因此直接求 $\min\{ \frac{sa_i-sb_i}{i} \}$ 就行。

由于询问的时 $f_1 \ge x$ 的个数，相当于就是 $\min\{ \frac{sa_i-sb_i}{i} \} \ge x$ 的个数，就是 $\forall i\in[1,n],\frac{sa_i-sb_i}{i} \ge x$。

变形一下 $sa_i\ge sb_i+xi$，不等式右侧都是定值。

直接用 dp 可以达到 $\text{O}(n^2m)$，要用前缀和优化，其中 $m$ 是 $a$ 的值域。

显然会超时。

发现 $sa_i\in[0,i\times m]$，所以当 $sb_i+xi\le0$ 即 $x \le -\frac{sb_i}{i}$ 时无论如何都会满足，答案为 $\prod(c_i+1)$。

同理，当 $sb_i+xi\ge im$ 即 $x \ge m-\frac{sb_i}{i}$ 时答案为 $0$。

当然，由于 $f_1$ 是取所有情况中的最小值，所以这里取的都是 $-\frac{sb_i}{i}$ 的最小值。

因此需要算的 $x$ 至多只有 $m$ 个，直接预处理就行。

复杂度 $\text O(n^2m^2)$。

[CF1438F] Olha and Igor

交互题。

给定一个高度为 h 的完全二叉树（恰好有 $n=2^h−1$ 个节点）。

你可以进行以下询问至多 $n+420$ 次。

选择三个互不相同的点 $u,v,w$，你需要保证 $1≤u,v,w≤n$。
交互库会返回当以 $w$ 为根时 $u$ 与 $v$ 的 lca。

你需要向交互库回答根的编号。

非常有意思的一道随机题。

思考一下询问 $u,v,w$ 后得到的点的某些性质，发现它一定是距离这三个点最近的一个点。

因此，对于一个点，选择它的概率大约为 $siz_{ls_u}\times siz_{rs_u} \times(n-siz_{ls_u}-siz_{rs_u})$。

然后聪明的你一定能一瞬间察觉被选择的可能性最大的点是根节点的左右儿子，在 $18\%$ 以上。其余的点最多的都不足 $10\%$，因此直接随机 $420$ 次，选取得到的次数最多的两个点。

若 $i=query(i,ls_1,rs_1)$，则 $i=1$，直接 $\text O(n)$ 遍历就行了。

[CF1152F2] Neko Rules the Catniverse

给定参数 $n,k,m$，你需要求有多少个大小为 $k$ 的序列 $a$ 满足如下三个条件：

任意两个元素其权值不同。
对于任意 $i$ 满足 $1\le i\le k$ 有 $1\le a_i\le n$。
对于任意 $i$ 满足 $2\le i\le k$ 有 $a_i\le a_{i-1}+m$。

对 $10^9+7$ 取模。

$1\le n\le 10^9$，$1\le k\le \min(n,12)$，$1\le m\le 4$。

非常有启发性的一道题。

发现 $m \le 4$ 这个条件非常有意思，复杂度应该与它有关，但是 $a_i$ 的范围可以取到 $[1,a_{i-1}+m]$，考虑怎么把范围缩减，比如 $[a_{i-1}+1,a_{i-1}+m]$ ？

很简单，可以考虑枚举 $1 \sim n$ 然后将每个数依次考虑是否塞进数组中，只有位于开头或者前一个数在 $[i-m,i-1]$ 间才可以。这个范围非常小，所以考虑状压 dp。

$dp_{i,j,S}$ 表示目前枚举到 $i$，数组中放了 $j$ 个数，$[i-m,i-1]$ 中的数是否存在与序列中。

\[dp_{i,j,S}\times (\text{popcount(S)+1})\to dp_{i+1,j+1,(S<<1) \& (2^m-1)+1} \]

\[dp_{i,j,S}\to dp_{i+1,j,(S<<1) \& (2^m-1)} \]

$n$ 非常大，但是 $2^m\times k$ 非常小，所以可以使用矩阵快速幂。

小 Y 的背包计数问题

有一个大小为 $n$ 的背包，并且小 $Y$ 有 $n$ 种物品。

对于第 $i$ 种物品，共有 $i$ 个可以使用，并且对于每一个 $i$ 物品，体积均为 $i$ 。

求把该背包装满的方案数为多少，答案对于 $23333333$ 取模。

非常经典的一道题。

显然可以根号分治。

对于 $i\le \sqrt n$ 的所有情况，直接 dp，但是不能使用 $01$ 背包，考虑完全背包，然后每轮结束后 $dp_{i,j}-dp_{i,j-i\times(i+1)}\to dp_{i,j}$。

对于 $i\ge \sqrt n$ 的情况，至多会选择 $\sqrt n$ 个数，显然可以随便选，没有个数限制。

这里有一个经典的套路，令 $f_{i,j}$ 表示选择了 $i$ 个数，总和为 $j$ 的方案数。

每次转移分以下两种情况：

加入一个 $\sqrt n+1$。
将选择过的所有数 $+1$。

容易发现可以覆盖所有情况。

[QOJ6355] 5

给定一个长度为 $n$ 的非负整数数组 $a$。计算满足以下条件的对 $(k,T)$ 的数量：存在一个长度为 $k$ 的 $a$ 的子序列，其和等于 $T$。
假设 $a$ 的元素之和等于 $S$，则保证 $a$ 中至少有 $\frac{S}{5}$ 个元素等于 $1$。

$1\le n,S \le 2\times 10^5$。

很有启发性的一道题。

发现 $1$ 的数量很多，可以考虑将所有数都减 $1$，此时就有至少 $\frac{S}{5}$ 个 $0$。

此时的 $f(k,T)$ 如果确定了 $T$ 的话 $k$ 的值一定可以组成若干个长度不少于 $\frac{S}{5}$ 的 $1$ 段。

所以可以使用 set 来维护对于不同的 $T$ 有哪些满足条件的 $k$ 段。

初始状态是 $dp_{0,0\sim cnt_0}=1$，可以使用二进制拆分来优化多重背包，想一想可以发现能够优化很多，复杂度好像是 $\text O(\sqrt m)$，但是我不会证。

[ICPC WF J]Bridging the Gap

$n$ 个人，桥的最大载重为 $m$，有一根火把，过桥必须使用火把。每次过桥的时间取决于这一组人中最慢的一个。

给定 $t$ 数组表示每个人的过桥时间。

求所有人过桥的最少时间。

思维路径十分奇妙的一道题。

首先贪心的想，每次过去的人一定是 $k$ 个最快的人和 $m-k$ 个最慢的人。$k$ 个最快的人是负责送火把回来的。

所以记录 $dp_{i,j}$ 表示排序后考虑前 $i$ 个人并且存了 $j$ 次往回走的最少时间。

转移的时候枚举这一组走了多少需要返回的人，$sum$ 表示前缀和。

一共有两种转移情况，一种是取 $k$ 个会返回的人和 $m-k$ 个直接过去的人，另一种是在 $i\le m$ 的情况下直接让过去了的人返回，然后再取一部分过去。

\[dp_{i,j}=\min_{k=0}^m\{ dp_{i-m+k,j-k+1}+sum_k+a_i\} \ \ \ \ \ \ \ \ when\ i\gt m \]

\[dp_{i,j}=\min_{k=0}^m\{ dp_{k,j-k+1}+sum_k+a_i\} \ \ \ \ \ \ \ \ when\ i\le m \]

[JOISC 2022] 复制粘贴 3

$X,Y$ 初始均为空串：

操作 A：输入字符 $c$，即将 $X$ 更新为 $X+c$。
操作 B：选择所有字符并剪切，即将 $Y$ 更新为 $X$，并将 $X$ 置为空串。
操作 C：将剪切板中的字符串粘贴到当前字符串末尾，即将 $X$ 更新为 $X+Y$。

计算出得到一个长度为 $N$ 的字符串 $S$ 需要花费多少时间。

$1\leq N\leq 2500$

区间 dp。

对于每个 $dp_{i,j}$，找到能包含 $k$ 个不重合的 $[i,j]$ 的最短的 $[p,j]$。

先不管怎么找，考虑算出这个后的 dp 式子。

\[\min(dp_{p,j},dp_{i,j}+B+C\times k+A\times(p-j+1-(j-i+1)\times k)) \to dp_{p,j} \]

当然，还有：

\[\min\{dp_{i+1,j}+A,dp_{i,j-1}+A,dp_{i,j}\}\to dp_{i,j} \]

复杂度为 $n^2\ln n$，区间的调和级数是这样的，我也不知道为什么。

接下来考虑怎么求 $p$。

令 $pre_{i,j}$ 表示能使 $[p,i-1]$ 包含 $[i,i+j-1]$ 的最大的 $p$。

这可以通过 $lcp$ 来求，而 $lcp$ 显然可以 $n^2$ 求出，具体来说就是若 $s_i=s_j$ 则 $lcp_{i,j}=lcp_{i+1,j+1}+1$。

[THUPC 2023 初赛] 背包

有 $n$ 种物品，第 $i$ 种物品单个体积为 $v_i$、价值为 $c_i$。

$q$ 次询问，每次给定 $V$，求体积为 $V$ 且必须装满的完全背包的最大价值。

$1 \le n \le 50, 1 \le v_i \le 10^5, 1 \le c_i \le 10^6, 1 \le q \le 10^5, 10^{11} \le V \le 10^{12}$。

同余最短路，以 $\frac{c_i}{v_i}$ 最大的 $i$ 的 $v_i$ 作为模数，不妨令 $i$ 为 $1$。

$dp_i$ 表示不考虑 $1$ 时对于模数为 $i$ 的背包方案中 $\sum c_i\times num_i-\lfloor\frac{\sum num_i\times v_i}{v_1}\rfloor \times c_1$ 的最大值。

最终的答案就是 $dp_{V\%v_1}+\lfloor\frac{V}{v_1}\rfloor\times c_1$。

由于每种不是 $1$ 的物品取走的数量一定小于 $v_1$，所以 $dp$ 求出的解中所用的体积一定小于 $\sum v_i\times v_1$ 也就是 $5\times 10^{10}$。因为 $10^{11}\le V \le 10^{12}$ 所以正确性可以满足。

接下来考虑同余最短路的过程。

发现在放 $i$ 的情况时，可以转移的所有情况构成了 $\gcd(v_i,v_1)$ 个环，图中不可能存在正环，因为多选 $1$ 显然有最优性，而如果能转圈就可以用一定数量的 $1$ 进行替代。

所以所有环直接跑两圈做完全背包就行了。

posted @ 2025-03-05 20:00 paper_zym 阅读(25) 评论(0) 收藏举报

刷新页面返回顶部

paper-book

纸书