chapter8-递归与分治

1.递归

递归，指直接或间接地调用自身，解决此类题目的方法见我之前走台阶的笔记，重点有2个，（1）分析问题，归纳出递归公式；（2）递归出口。就像俄罗斯套娃一样，要让递归调用总体朝向递归出口推进。

n的阶乘

//递归-n的阶乘 2024-03-08
#include <iostream>
#include <cstdio>
 
using namespace std;
 
long long Factorial(int n) {
    if(0 == n) {
        return 1;
    } else {
        return n * Factorial(n - 1);
    }
}
 
int main()
{
    int n;
    while(cin >> n) {
        cout << Factorial(n) << endl;
    }
    return 0;
}

汉诺塔问题

用递归策略来处理常规的汉诺塔问题，即把左边的从小到大的圆圈移到右边任意一个空的柱子上，如图所示。设把n个圆圈按照限制挪到最右边的空柱子上，需要的总步数为$f_n$，那么现在我们要将最大的圆圈挪到最右边这个柱子上，首先要把$n-1$个圆圈挪到中间的柱子上，这一步需f_n-1步骤数。

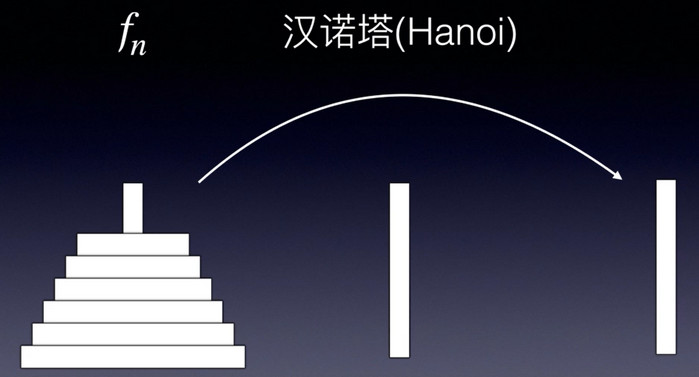
再把大圆圈挪到最右边的柱子上，需$1$步骤数，由于此时最右边柱子上的圆圈是最大的，所以不存在限制，可以看成是一个空柱子，**此时再把中间的$n-1$个圆圈挪到右边柱子上，需f_n-1步骤数。

分析之后，得到递归公式：f_n = 2 * f_n-1 + 1
递归出口：$f_1=1$

如果考试的时候你能根据递归公式推出通项表达式，进而总结出公式$f_n=2^n-1$，那么直接套公式即可，如果不行，建议还是用递归做比较好。

汉诺塔(Hanoi)

//常规汉诺塔问题 2024-03-08
#include <iostream>
#include <cstdio>
 
using namespace std;
 
long long Hanoi(int n) {
    if(n == 1) {
        return 1;
    } else {
        return 2 * Hanoi(n - 1) + 1;
    }
}
 
int main()
{
    int n;
    while(cin >> n) {
        cout << Hanoi(n) << endl;
    }
    return 0;
}

HDU OJ 2064 汉诺塔III

汉诺塔III
设把最左边柱子的$n$个圆圈，经过中间的空柱子，再放到最右边的空柱子，所需要的总步数为$f_n$。那么我们先把$n-1$个圆圈放到最右边的柱子上就需要步骤数f_n-1；把最大的圆圈挪到中间的柱子上，需要$1$步；再把最右边的$n-1$个圆圈从最右边挪到最左边，需要f_n-1步；此时把最大的圆圈放到最右边，需要$1$步。

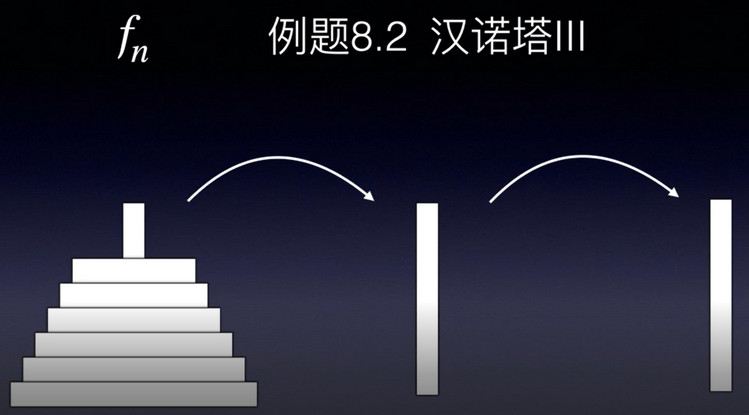
此时最右边的柱子上只有一个最大的圆圈，不受限制，可以看成是一个空柱子，故此时把最左边的$n-1$个圆圈移到最右边，需要步数f_n-1。

得到递归公式：f_n = 3 * f_n-1 + 2
递归出口：考虑基础情况，只有一个大圆圈($n=1$)在最左边，把它移到最右边需要$2$步

汉诺塔III(Hanoi)

//递归-汉诺塔III 2024-03-08
#include <iostream>
#include <cstdio>
 
using namespace std;
 
long long Hanoi3(int n) {
    if(n == 1) {
        return 2;
    } else {
        return 3 * Hanoi3(n - 1) + 2;
    }
}
 
int main()
{
    int n;
    while(cin >> n) {
        cout << Hanoi3(n) << endl;
    }
    return 0;
}

2.分治

分治策略是另一个非常重要的算法，字面解释就是把一个复杂的问题分成两个或更多个子问题，子问题之间互相独立且与原问题相同或相似。与贪心策略不同，如果子问题仍然不好求解，可以继续再把子问题分成更小的子问题，直到最后的子问题可以简单地直接求解。

由于分治法产生的子问题往往与原问题相同且模式更小，这就为使用递归策略求解提供了条件。在从过程中会导致了递归过程的产生。

分治法的步骤与贪心策略极其相似：

求解Fibonacci

Fibonacci数列的求解有三种方法，分别是：

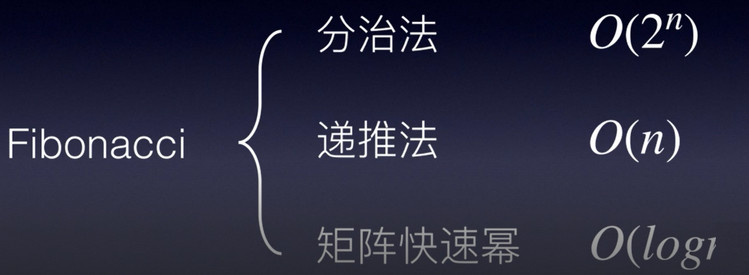
2.1.1 分治法求解Fibonacci

非常低效，但可以用来理解分治法的精髓，低效的原因是有大量的重复计算，如果我们直接把每一个Fibonacci数列值从小到大保存到一个数组中，那么就是递推法，时间复杂度还不错。

注意，分治法通常会采用分治法进行求解。

分治法求Fibonacci

//分治法-Fibonacci 2024-03-08
#include <iostream>
#include <cstdio>
 
using namespace std;
 
int Fibonacci(int n) {
    if(n == 0 || n == 1) {
        return n;
    } else {
        return Fibonacci(n - 1) + Fibonacci(n - 2);
    }
}
 
int main()
{
    int n;
    while(cin >> n) {
        cout << Fibonacci(n) << endl;
    }
    return 0;
}

2.1.2 递推法求解Fibonacci

递推法求Fibonacci

//递推法-Fibonacci 2024-03-08
#include <iostream>
#include <cstdio>
 
using namespace std;
 
const int MAXN = 35;
int Fibo[MAXN];
 
void Initial()
{
    Fibo[0] = 0;
    Fibo[1] = 1;
    for(int i = 2; i < MAXN; ++i) {
        Fibo[i] = Fibo[i-1] + Fibo[i-2];
    }
}
 
int main()
{
    Initial();
    int n;
    while(cin >> n) {
        cout << Fibo[n] << endl;
    }
    return 0;
}

2.1.2 矩阵快速幂求解Fibonacci

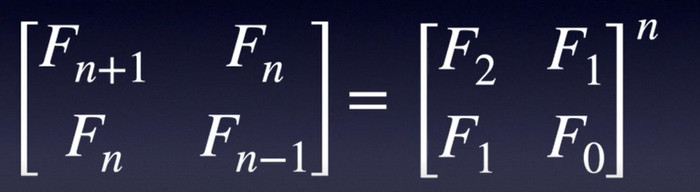
公式推导：
用数学归纳法的方式

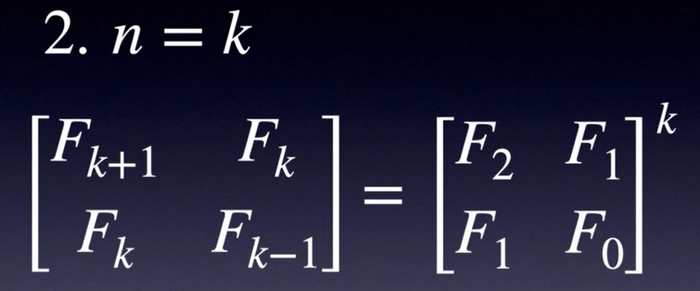
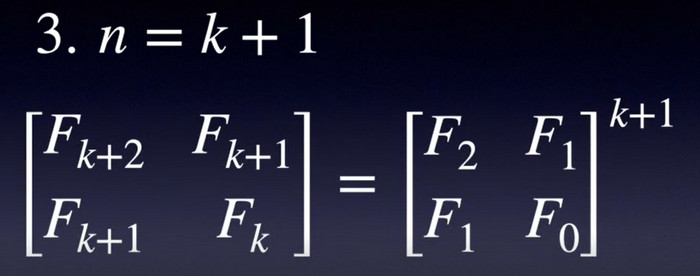
矩阵快速幂求Fibonacci

//矩阵快速幂-Fibonacci 2024-03-08
#include <iostream>
#include <cstdio>
 
using namespace std;
 
const int MAXN = 10;
 
struct Matrix {
    int matrix[MAXN][MAXN];
    int row, col;
    Matrix() {}
    Matrix(int r, int c): row(r), col(c) {}
};
 
Matrix Multiply(Matrix x, Matrix y) {
    Matrix answer = Matrix(x.row, y.col);
    for(int i = 0; i < answer.row; ++i) {
        for(int j = 0; j < answer.col; ++j) {
            int sum = 0;
            for(int k = 0; k < x.col; ++k) {
                sum += x.matrix[i][k] * y.matrix[k][j];
            }
            answer.matrix[i][j] = sum;
        }
    }
    return answer;
}
 
Matrix QuickPower(Matrix x, int n) {
    Matrix answer = Matrix(x.row, x.row);
    for(int i = 0; i < answer.row; ++i) {
        for(int j = 0; j < answer.col; ++j) {
            if(i == j) {
                answer.matrix[i][j] = 1;
            } else {
                answer.matrix[i][j] = 0;
            }
        }
    } 
    //快速幂
    while(n > 0) {
        if(n % 2 == 1) {
            answer = Multiply(answer, x);
        }
        n /= 2;
        x = Multiply(x, x);
    }
    return answer;
}
 
int main()
{
    int n;
    Matrix start(2,2);
    start.matrix[0][0] = 1;
    start.matrix[0][1] = 1;
    start.matrix[1][0] = 1;
    start.matrix[1][1] = 0;
    Matrix answer(2,2);
    while(cin >> n) {
        answer = QuickPower(start, n);
        cout << answer.matrix[0][1] << endl; //matrix[0][1]和matrix[1][0]一样
    }
    return 0;
}

例题8.4 二叉树

求根结点为m的树中有多少结点数目问题

//分治-二叉树结点m所在子树总共有几个结点 2024-03-08
#include <iostream>
#include <cstdio>
 
using namespace std;
 
int NodeNumber(int m, int n) {
    if(m > n) {
        return 0;
    } else { //注意要加m结点本身，拆成子问题，m结点的左右子树+m结点本身
        return 1 + NodeNumber(2 * m, n) + NodeNumber(2 * m + 1, n);
    }
}
 
int main()
{
    int m, n;
    while(cin >> m >> n) {
        cout << NodeNumber(m, n) << endl;
    }
    return 0;
}

当结点m大于n时，以m为根结点的树为空，该数的结点数目必定为0，这个便是这个问题可被轻松求解的底层问题，也是递归出口。