chapter7-贪心策略-区间贪心

2.区间贪心

区间贪心也是一种常见的贪心策略类的题型。它是指当有多个不同的区间存在，且这些区间有可能相互重叠的时候，如何选择才能从众多区间中，选取最多的两两互不相交的区间。

今年暑假不AC

杭电 OJ 2037

看尽可能多的节目：贪心策略

问题分析：区间贪心和简单贪心不同的地方在于决定怎么贪，题目给了我们节目的开始时间、结束时间、持续时间，本题的贪心策略是什么呢，使得当前子问题获得最优解？

显然，（1）开始时间最早、（2）持续时间最短，都可以想到特例不满足题目的最优解。

（3）结束时间最早，这就是本题需要的贪心策略，因为结束时间越早，剩下的时间就越多，可选择的节目余地就越多，这样就获得了当前子问题的最优解。

今年暑假不AC

//区间贪心学习-看尽可能多的节目 2024-03-07
#include <iostream>
#include <cstdio>
#include <algorithm>
 
using namespace std;
 
const int MAXN = 100 + 10;
 
struct program {
    int start_time;
    int end_time;
};
program arr[MAXN];
 
bool Compare(program a, program b) {
    return a.end_time < b.end_time;
}
 
int main()
{
    int n;
    while(cin >> n) {
        if(0 == n) {
            break;
        }
        for(int i = 0; i < n; ++i) {
            cin >> arr[i].start_time >> arr[i].end_time;
        }
        sort(arr, arr + n, Compare);
        int current = 0;
        int answer = 0;
        for(int i = 0; i < n; ++i) {
            if(current <= arr[i].start_time) {
                current = arr[i].end_time;
                ++answer;
            }
        }
        cout << answer << endl;
    }
    return 0;
}

POJ 1328 Radar Installation

POJ 安装雷达

题目的诉求，以及该怎么贪

尽可能少的雷达站：贪心策略

问题分析：在海岸线的某个点安装一个雷达，便可以以这个点为圆心，以$d$为半径作为覆盖范围；海岸线是无线长的一条直线，而岛屿是有限个(<=1000)。

如果我们从海岸线的角度来思考这个问题实际上非常困难，因为海岸线上有无数个点，如何抉择安装位置很难。在海岸线的哪些点上安装雷达能覆盖全部的岛屿。

所以要转换一下问题，从岛屿的角度思考问题，要覆盖这个岛屿，你必须在海岸线的哪个位置装雷达。

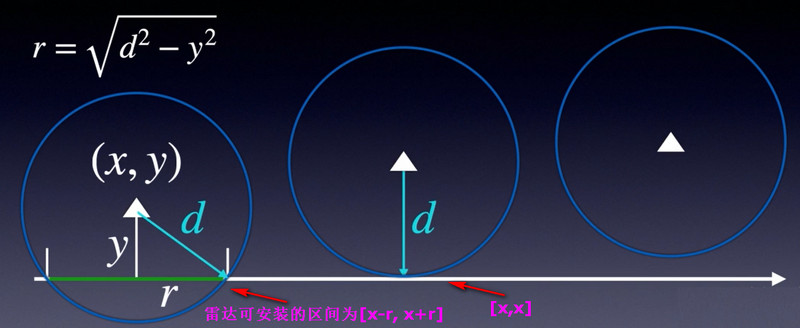
区间尽可能重叠的情况下，安装尽可能少的雷达。

Radar Installation

//区间贪心学习-安装尽可能少的雷达 2024-03-07
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cmath>
 
using namespace std;
 
const int MAXN = 1000 + 10;
 
struct avail {
    double start_pos;
    double end_pos;
};
avail arr[MAXN]; //保存区间
 
bool Compare(avail a, avail b) {
    return a.start_pos < b.start_pos; //区间尽可能重叠
}
 
int main()
{
    int n, d, x, y;
    int caseNumer = 0;
    while(cin >> n >> d) {
        if(0 == n && 0 == d) {
            break;
        }
        bool flag  = true;
        for(int i = 0; i < n; ++i) {
            cin >> x >> y;
            if(y <= d) {
                double r = sqrt((double)d * d - y * y);
                arr[i].start_pos = x - r;
                arr[i].end_pos = x + r;
            } else {
                flag = false;
            }
        }
        if(!flag) {
            printf("Case %d: %d\n", ++caseNumer, -1);
        } else {
            sort(arr, arr + n, Compare);
            double current = arr[0].end_pos;
            int answer = 1;
            for(int i = 1; i < n; ++i) {
                if(arr[i].start_pos <= current) {
                    current = min(current, arr[i].end_pos);
                } else { //没有重叠
                    current = arr[i].end_pos;
                    ++answer;
                }
            }
            printf("Case %d: %d\n", ++caseNumer, answer);
        }
    }
    return 0;
}

注意，代码中用到的sqrt函数、ceil函数、floor函数，均需要调用cmath，并且输入的参数必须为浮点数类型，如果是整数，就要强制转换或者乘上$1.0$