有依赖的背包问题(分组背包)

有依赖的背包问题(分组背包)

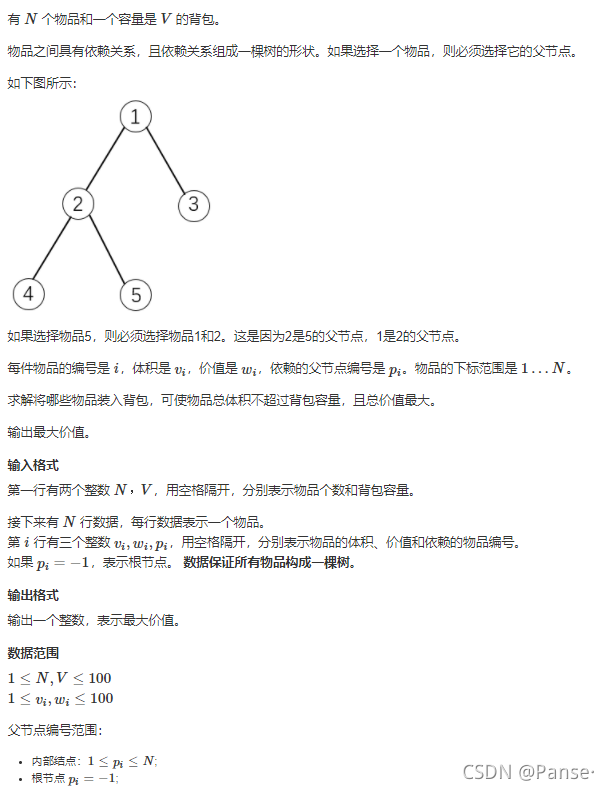
自底向上放入背包
样例输入：

5 7
2 3 -1
2 2 1
3 5 1
4 7 2
3 6 2

样例输出：

11

代码模板：

//转换为分组背包问题
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;

const int N = 110;

int n, m;
int h[N], e[N], ne[N], idx;
int v[N], w[N];
int f[N][N]; //以 i 为root，体积为 j 的最大价值

void add(int p, int i) {
    e[idx] = i;
    ne[idx] = h[p];
    h[p] = idx++;
}
//从叶子节点往父节点递归
void dfs(int u) {
    for (int i = h[u]; i != -1; i = ne[i]) {//循环物品组
        int son = e[i];
        dfs(son);
        
        //分组背包
        for (int j = m - v[u]; j >= v[son]; j--)  //循环体积
            for (int k = v[son]; k <= j; k++)     //循环决策
                f[u][j] = max(f[u][j], f[u][j - k] + f[son][k]);
                
    }
    
    //将物品u放进去
    for (int i = m; i >= v[u]; i--)
        f[u][i] = f[u][i - v[u]] + w[u];
        
    for (int i = 0; i < v[u]; i++)
        f[u][i] = 0;
        
}

int main(){
    memset(h, -1, sizeof h);
    cin >> n >> m;
    int root;
    for (int i = 1; i <= n; i++) {
        int p;
        cin >> v[i] >> w[i] >> p;
        if (p == -1) {
            root = i;
        }
        else {
            add(p, i);
        }
    }
    dfs(root);
    cout << f[root][m] << endl;
    return 0;
}

---