Dijkstra

Dijkstra求最短路I

输入样例：

3 3
1 2 2
2 3 1
1 3 4

输出样例：

3

模板：

//Dijkstra 求最短路 I
//稠密用邻接矩阵
//单源最短路 
#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm> 
using namespace std;
const int N = 510;
int n,m;
int g[N][N];  //邻接矩阵
int dist[N];
bool st[N];
int dijkstra(){
	memset(dist,0x3f,sizeof dist);
	
	dist[1]=0;
	
	for(int i=0;i<n;i++){
		int t=-1;
		for(int j=1;j<=n;j++)
			if(!st[j]&&(t==-1||dist[t]>dist[j]))
			    t=j;    //直接走近路 
        

		st[t]=true;
		
		for(int j=1;j<=n;j++)
			dist[j]=min(dist[j],dist[t]+g[t][j]); // 起点到j的最小距离
			
	}
	if(dist[n]==0x3f3f3f3f) return -1;
	return dist[n];
}
int main(){
	scanf("%d%d",&n,&m);
	
	memset(g,0x3f,sizeof g);
	
	while(m--){
		int a,b,c;
		scanf("%d%d%d",&a,&b,&c);
		g[a][b]=min(g[a][b],c);
	}
	
	int t=dijkstra();
	
	printf("%d\n",t);
	
	return 0;
} 

---

 

---

Dijkstra求最短路II

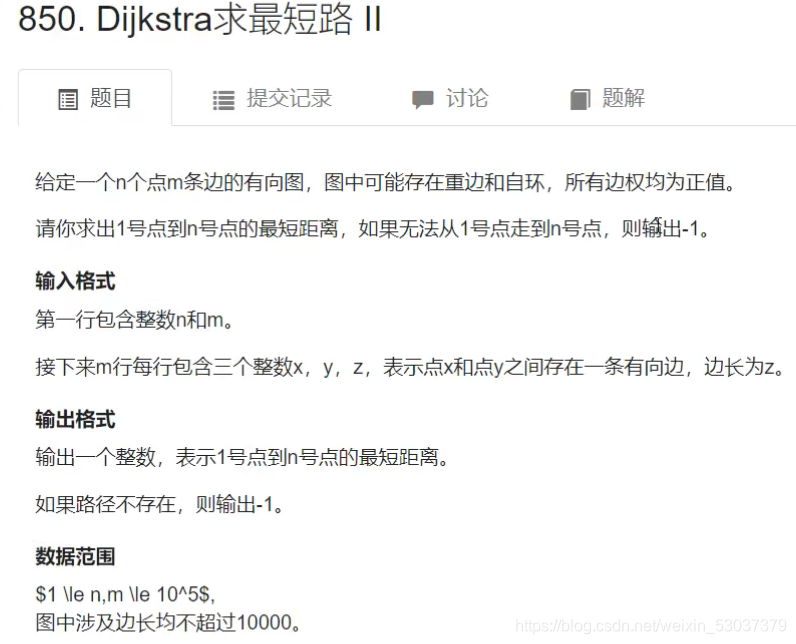
它能够在 O(logn)（其中 n 为堆中的元素数量）的时间复杂度内完成插入、删除最小值的操作，在 O(1) 的时间复杂度内完成取堆内最小值的操作。于是我们可以将上面的查找这一步操作放入到堆中，时间复杂度就能下降到 O(logn)。
小根堆一共n个点每次更新 O(logn) 一条边就要更新一个点，一共m条边 -> mlogn
输入样例：

3 3
1 2 2
2 3 1
1 3 4

输出样例：

3

模板：

// 堆 优 化 
//邻接表 
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
const int N = 150010;
typedef pair<int,int> PII;  //稀疏用邻接表
int e[N],ne[N],w[N],h[N],idx;
int dist[N];
int n,m;
bool st[N];
void add(int a,int b,int c){
	e[idx]=b;
	w[idx]=c;
	ne[idx]=h[a];
	h[a]=idx++;
}
int dijkstra(){
	memset(dist,0x3f,sizeof dist);
	dist[1]=0;
	
	//priority_queue<Type, Container, Functional> 
	//pair的比较，先比较第一个元素，第一个相等比较第二个
	priority_queue<PII,vector<PII>,greater<PII>> heap;  //小根堆 
	heap.push({0,1});
	
	while(heap.size()){
		auto t=heap.top();
		heap.pop(); 
		
		int distance=t.first,ver=t.second;
		if(st[ver]) continue; //dijkstra 出队判重
		st[ver]=true;  
		for(int i=h[ver];i!=-1;i=ne[i]){
			int j=e[i];
			if(dist[j]>distance+w[i]){
				dist[j]=distance+w[i];
				heap.push({dist[j],j}); 
			}
		}
	}
	if(dist[n]==0x3f3f3f3f) return -1;
	return dist[n];
}
int main(){
	scanf("%d%d",&n,&m);
	
	memset(h,-1,sizeof h);
	
	while(m--){
		int a,b,c;
		scanf("%d%d%d",&a,&b,&c);
		add(a,b,c);
	}
	
	int t=dijkstra();
	
	printf("%d\n",t);
	
	return 0;
}

---