莫队

莫队算法最初是由清华集训队莫涛队长在\(2009\)年整理后详细提出，是一种离线算法，主要是利用双指针，再基于分块思想解决一些区间查询问题，又被称为“优雅的暴力算法”。
时间复杂度为\(O((m+n)*sqrt(n))\)。

引例：给出一个\(n\)个数的序列和\(m\)次区间询问，问\([l，r]\)中有多少个不同的数？

首先想到可以用\(unique\)函数在\(O(n)\)的复杂度下求到去重后的元素个数，时间复杂度是\(O(m*n)\)

对于莫队，我们要把一个区间的答案转移到与之相邻的区间中去(这里的相邻指的是左右区间端点l或r，左或右移动一格)，怎么做呢？我们用一个数组\(Cnt\)来记录每个数出现的次数，\(cur\) 表示当前区间的答案，例如：

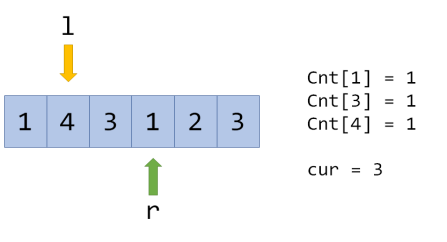
现在转移到紧邻的区间就很简单了，例如转移到\([l,r+1]\)：

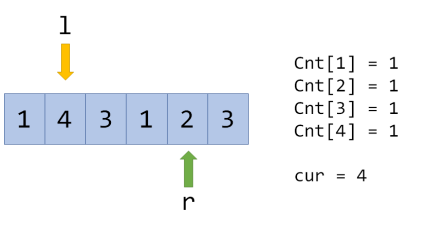
\(Cnt[2]=0\)，说明添加了一个没出现过的数，所以\(cur\)变成\(4\)，但如果在这里再次向右转移：

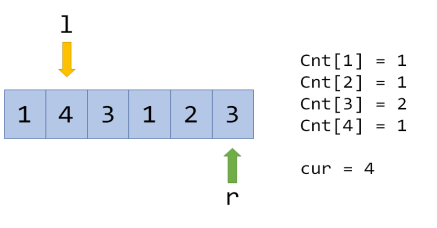
刚才出现的都是区间扩大，如果区间缩小呢？比如左端点\(l\)向右移一位：

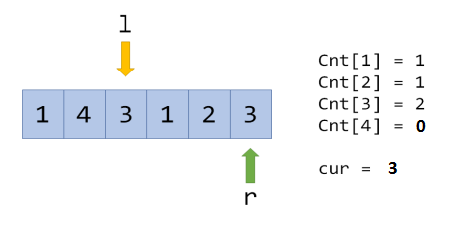
通过上述图片的模拟，我们可以轻松写出在区间移动时，更新统计数组cnt和cur的两个扩大区间和减小区间的函数：

//扩大
void add(int x) {
    if(!cnt[a[x]]) sum++;
    cnt[a[x]]++;
}

//减小
void del(int x) {
    if(cnt[a[x]]==1) sum--;
    cnt[a[x]]--;
}

那么从任意一个区间移动到另一个区间，只需写：

    while(nowl < q[i].l) del(nowl++);
    while(nowl > q[i].l) add(--nowl);
    while(nowr < q[i].r) add(++nowr);
    while(nowr > q[i].r) del(nowr--);

注意\(++\)和\(--\)的位置。删数是先删后移，添数是先移后添。初始化时，要先令\(l = 1\)，\(r = 0\)。

现在我们可以从一个区间的答案转移到另一个区间了，但是，如果直接在线查询，很有可能在序列两头“左右横跳”，到头来最坏可能还不如朴素算法\(O(m*n)\)
我们可以把查询搞成离线的，然后对m个查询排个序。使得左右区间的移动更少。如何排序？

1. 按左区间从小到大，左区间相同时按右区间从小到大。
   仔细思考后，依然不理想！
2. 把n个数均分成\(\sqrt{n}\)个块，那么每个块里就有\(\sqrt{n}\)个元素，若左端点在同一个块，按右端点从小到大排序，若左端点不在同一个块，按左端点从小到大排序。这就是普通莫队算法的排序方法

int block(int x) {  return x / sqrt(n); }

int cmp(node a,node b) {
    if(block(a.l) != block(b.l)) 
        return a.l < b.l;
    else return a.r < b.r;
}

时间复杂度分析：
把n个数均分成\(\sqrt{n}\)个块，那么每个块里就有\(\sqrt{n}\)个元素

我们先来分析右指针的移动次数，由于每个块里的右指针是有序的，所以每个块里左指针配对的右指针最多移动 \(n\) 次，一共有\(\sqrt{n}\)个块，所以右指针实际移动总数为\(n*\sqrt{n}\) 次；

再考虑左指针，每个块里左指针假设均分为\(\dfrac{m}{\sqrt{n}}\)个，每个都是无序的，假设每个都移动\(\sqrt{n}\)次，那么在一个块中，左指针就移动\(m\)次，一共有\(\sqrt{n}\)个块，所以左指针共移动\(m*\sqrt{n}\)次，把左右指针的移动次数加起来就是总的时间复杂度\(O((m+n)*\sqrt{n})\)。


这样的时间复杂度很有可能被卡常！
所以还可以做一个神奇的优化：

奇偶性优化

简单地说，如果左指针在奇数块，就让右指针从左至右排序；如果左指针在偶数块，就让右指针从右至左排序。这样奇偶交替，奇数块后右指针会停在最右边，更好的作为偶数块右指针从右至左的起点，反之一样

int block(int x) {
    return x/sqrt(n);
}
int cmp(node a,node b) {
    if(block(a.l) ^ block(b.l)) //^相当于!=
        return a.l<b.l;
    else {
    	if(block(a.l)&1) return a.r<b.r;
    	else return a.r>b.r;
	}
}

综合一下，就可以\(A\)掉这道题

#include<bits/stdc++.h>
using namespace std;
struct node {
    int l,r,id;
}q[200020];

int a[50050],cnt[1000010],n,m,sum,ans[200020];
int block(int x) {
    return x/sqrt(n);
}
int cmp(node a,node b) {
    if(block(a.l)!=block(b.l)) 
        return a.l<b.l;
    else {
    	if(block(a.l)&1) return a.r<b.r;
    	else return a.r>b.r;
	}
}
void add(int x) {
    if(!cnt[a[x]]) sum++;
    cnt[a[x]]++;
}

void del(int x) {
    if(cnt[a[x]]==1) sum--;
    cnt[a[x]]--;
}

int main() {
    scanf("%d",&n);
    for(int i=1;i<=n;i++)  scanf("%d",&a[i]);
    scanf("%d",&m);
    for(int i=1;i<=m;i++) {
        scanf("%d%d",&q[i].l,&q[i].r);
        q[i].id=i;
    }
    sort(q+1,q+m+1,cmp);
    int nowl=1,nowr=0;
    for(int i=1;i<=m;i++) {
        while(nowl<q[i].l) del(nowl++);
        while(nowl>q[i].l) add(--nowl);
        while(nowr<q[i].r) add(++nowr);
        while(nowr>q[i].r) del(nowr--);
        ans[q[i].id]=sum;
    }
    for(int i=1;i<=m;i++) printf("%d\n",ans[i]);
    return 0;
}