最大子段和の解法

前缀和

皆用此题
首先打出一份$O(n^3)$的暴力代码

for(int l = 1;l <= n; l++) 
	for(int r = l;r <= n ;r++) {
		sum=0;
		for(int k = l;k <= r;k++) 
			sum += a[k];
		ans = max(sum, ans);
	}

可发现$k$循环可以用前缀和浅优化一下

for(int l = 1;l <= n; l++) 
	for(int r = l;r <= n ;r++) 
		ans=max(ans, sum[r]-sum[l-1]);

$O(n^2)$肯定还是过不了
考虑固定右端点，此时若要最大就要让左端点的前缀和最小，这样在每一步更新一下最小的前缀和即可。

for (int i = 1; i <= n; ++i) {
    sum += a[i];//sum表示前缀和
    ans = max(ans, sum - mn);//统计答案
    mn = min(mn, sum);//取最小值
}

这样时间按复杂度就降到$O(n)$了

$\mathcal{kandane}$ 算法

枚举$a$数组，用$cur$记录当前最大值。
如果当前循环到$i$时$cur$ $<$ $0$，那么显然$a_i$ $<$ $a_i$ $+$ $cur$。所以清零$cur$,舍弃前面的所有元素从$i$重新开始计算。
时间复杂度$O(n)$

for (int i = 1; i <= n; ++i) {
	scanf("%d", &a);
	cur += a;
	ans = max(ans, cur);
	if (cur < 0) cur = 0;
}

对于环形最大子段和也可用$kandane$解决
以这道题为例

首先对于环上的最大子段和，在长度为$n$的序列中，有哪些情况？

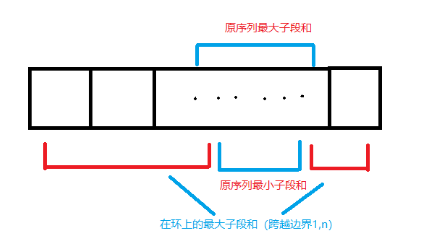
思路就很清晰了，$ans$ $=$ $max$$($最大子段，总和 $-$ 最小子段$)$

for(int i = 1;i <= n;i++) {
	tot += a[i];
	//最大
	sum1 += a[i];
	ans1 = max(ans1, sum1);
	if(sum1 < 0) sum1 = 0;
	//最小
	sum2 += a[i];
	ans2 = min(ans2,sum2);
	if(sum2 > 0) sum2 = 0;
}
printf("%d", max(ans1, tot - ans2));

求最大子矩阵也同样。比如这道
就是把一维里的$a_i$看做这里每一行的一段和(用前缀和预处理)
固定矩阵的列，每一次用前述方法增加一行（就像$a_i$）

for (int i = 1; i <= n; i++) {
     for (int j = 1; j <= n; j++) {
        cin >> a[i][j];
        a[i][j] += a[i][j - 1];
    }
}
for (int i = 0; i < n; i++)
    for (int j = i + 1; j <= n; j++) {
        int maxn = 0;
        for (int k = 1; k <= n; k++) {
            maxn += a[k][j] - a[k][i];
            ans = max(ans, maxn);
            if (ans < 0) ans = 0;
        }
    }