图论の题（内含Kuglarz，棋盘上的守卫,走廊泼水节）

Kuglarz

首先，有一个比较明显的结论:

必须要知道每一个位置的奇偶性，才能知道所有位置有没有小球。

再仔细一想，每一个位置的奇偶性可以有两种方法推出来：

• 直接花费 a_i,i 得到；
• 花费两个区间的价值 a_i,j+a_i+1,j 得到。

可是区间的价值又可以从两个区间推来，那就很难处理了。

考虑把点权变成边权，把位置 i变成 i-1与 i之间的一条边。

也就是说，我们要知道所有相邻点之间边的信息。

而之前已经的得到两种推出位置奇偶性的方法，可以用下图的两种方法表示：

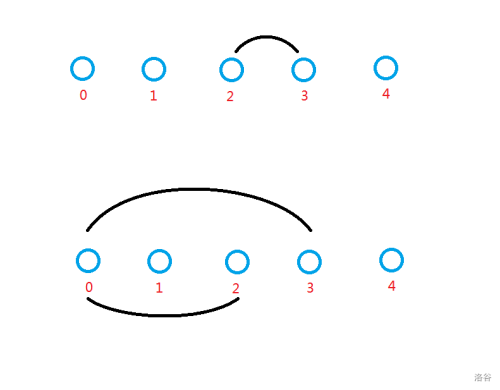
以上两种方法都可以得到 2 和 3 之间那个位置的信息。

总结一下，就是说，我们要连边，使每个点都被连到。

求最小生成树。

 

Code

 #include <bits/stdc++.h>
using namespace std;
typedef long long ll;
struct Edge {
	ll u,v,w;
}edge[5000005];
ll fa[5000005];
bool cmp(Edge x,Edge y) {
	return x.w<y.w;
}
ll Find(ll x) {
	if(x==fa[x]) return x;
	return fa[x]=Find(fa[x]);
}
int main() {
	//freopen("kuglurz.in","r",stdin);
	//freopen("kuglurz.out","w",stdout); 
	ll n,a,idx=0;
	scanf("%lld",&n);
	for(ll i=1;i<=n;i++)
		fa[i]=i;
	for(ll i=1;i<=n;i++) {
		for(ll j=i;j<=n;j++) {
			scanf("%lld",&a);
			edge[++idx].u=i-1,edge[idx].v=j,edge[idx].w=a;
		}
	}
	sort(edge+1,edge+idx+1,cmp);
	ll sum=0,cnt=0;
	for(ll i=1;i<=idx;i++) {
		ll x=Find(edge[i].u),y=Find(edge[i].v);
		if(x==y) continue;
		cnt++;
		fa[x]=y;
		sum+=edge[i].w; 
		if(cnt==n) break;
	}
	printf("%lld",sum);
	return 0;
}

 

走廊泼水节

  

 题目分析

  看到题面，我们首先需要知道完全图是什么。度娘如是说道：“完全图是一个简单的无向图，其中每对不同的顶点之间都恰连有一条边相连”。相当于题目给了你一颗子树，让你填充。倒着想，如果给了你一颗完全图求最小生成树，你会怎么求？先从小到大排序。然后你会发现对于最小生成树的每两个，如果在完全图中还存在另一边（最小生成树中不包含），那么这一边一定比对于这两点在最小生成树的任意边小。倒回来，你填充的任意边必须比这两点连通的边大。

首先我们设S_x表示为x之前所在的连通块 那么S_y表示为y之前所在的连通块.
假如说点A属于S_x这个集合之中 点B属于S_y这个集合之中.  那么点A与点B之间的距离,必须要大于之前的w,否则就会破坏之前的最小生成树，所以说(A,B)之间的距离最小为w+1。假如说我们知道S_x有p个元素,然后S_y有q个元素。那么将Sx与Sy连通块的所有点相连.显然这个两个连通块会增加.p×q−1条边。然后每一条边的最小长度都为w+1。

所以我们会得出
(w+1)×(p∗q−1)为两个连通块成为完全图的最小代价

 

Code

 #include <bits/stdc++.h>
using namespace std;
int s[6005],fa[6005];
struct Edge {
	int u,v,w;
}edge[6005];
bool cmp (Edge x,Edge y) {
	return x.w<y.w;
}
int Find(int x) {
	if(fa[x]==x) return x;
	return fa[x]=Find(fa[x]);
}
int main() {
	int t;
	scanf("%d",&t);
	while(t--) {
		int n;
		scanf("%d",&n);
		for(int i=1;i<=n;i++) 
			fa[i]=i,s[i]=1;
		for(int i=1;i<n;i++) {
			scanf("%d %d %d",&edge[i].u,&edge[i].v,&edge[i].w);
		}
		sort(edge+1,edge+n,cmp);
		int ans=0;
		for(int i=1;i<n;i++) {
			int x=Find(edge[i].u),y=Find(edge[i].v);
			if(x==y) continue;
			fa[x]=y;
			ans+= (edge[i].w+1) * (s[x]*s[y]-1);
			s[y]+=s[x];
		}
		printf("%d\n",ans);
	}
	return 0;
}

 

棋盘上的守卫

  在( i,j )这个点上我们可以放置两种守卫，第一种是横向守卫，第二种是竖向守卫，所以它们之间只能选择一种，可以抽象成一条边，链接的是横向的第 i 个阶段，竖向的第 j 个阶段，为了方便，我们将 j的下标写作j + n。

可以得到一条性质： 对于任意一个点 i， 若 i > n，则这是列的阶段。

• 将行列看成 n+m个点。将每个格点放置守卫看成所在行列连了一条边，然后把每条边定向，如果被指向表示当前格点对当前 行/列 进行了保护。

• 这样就会有 n+m个点，n+m条有向边，同时每条边最多有 1 的入度。形成了基环树森林。

如果当前两个点在同一集合，那么判断是否已经成环，如果不成环还可以加上这一条边。
如果当前两个点不在同一个集合，那么判断是否存在一个点所在集合没有成环，如果是，可以加边。

 //基环树 
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
struct Edge {
    ll u, v, w;
} edge[100005];
ll fa[100005];
bool vis[100005];
ll Find(ll x) {
    if (x == fa[x])
        return x;
    return fa[x] = Find(fa[x]);
}
bool cmp(Edge x, Edge y) { return x.w < y.w; }
int main() {
    ll n, m, a, idx = 0;
    scanf("%lld %lld", &n, &m);
    for (ll i = 1; i <= n; i++) {
        for (ll j = 1; j <= m; j++) {
            scanf("%lld", &a);
            edge[++idx].u = i, edge[idx].v = j + n, edge[idx].w = a;
        }
    }
    for (ll i = 1; i <= m + n; i++) {
        fa[i] = i;
    }
    sort(edge + 1, edge + idx + 1, cmp);
    ll ans = 0;
    for (ll i = 1; i <= idx; i++) {
        ll x = Find(edge[i].u), y = Find(edge[i].v);
        if (vis[x] && vis[y]) { //如果已经成环
            continue;
        } else if (x == y) { //如果在一个集合,连一条边可以成环 
            vis[y]=vis[x] = 1;//记录这两边已经成一个环 
            ans += edge[i].w;
        } else {
            fa[x] = y; 
            ans += edge[i].w;
            vis[y] = vis[y] | vis[x];//如果原x或y与别的树成环 ，记录y是已成环树 
        }
    }
    printf("%lld", ans);
    return 0;
}