HERS: Homomorphically Encrypted Representation Search-2020:学习
阅读“HERS: Homomorphically Encrypted Representation Search-2020”,记录笔记。
摘要

- 本文介绍了一种针对加密图像的搜索方法。首先提取图像特征,然后压缩特征,接着加密特征,随后在加密域中进行搜索,最后解密结果。
- 其中:against a large gallery(大型图像集)、fixed-length representation(定长表示)
- 效果:在1亿张加密图像中搜索需要500s,比最新的方法快275倍。
引言

- 数据泄漏严重,所以发展加密技术很重要。
- 虽然常用的加密技术已经广泛使用,比如AES加密,但针对图像的这种特殊类型的加密并不适用,比如图像搜索,虽然用AES加密图像,但在搜索时仍需解密,所以针对图像搜索所需的加密技术很重要。

- 虽然在增强图像识别度(人脸识别)、图像分类方面做了很多研究,但针对图像的安全方面考虑的就比较少。
- 对于人脸识别,可以通过人脸挖掘出年龄、种族、性别等属性就有些侵犯用户隐私了,通常采取提取局部特征来解决,比如深度学习中的CNN表示,可以转换到高质量的图像。


- HE就能很好地解决该问题,因为在特征提取后,一般使用计算特征之间距离进行比较,比如:欧几里得距离和余弦相似度,其中涉及加法和乘法运算。
- 使用现有的FHE方案,需要考虑计算复杂度。比如在匹配一对512维的加密图像时,需要48.7M内存和12.8s,且只能适用于1:1匹配,并不适用于大规模的1:n匹配。


- 本文通过特征降维和使用高效的FHE算法实现了1:n高效匹配。
- 创新点:(1)使用SIMD,实现密文打包,对于1亿张512维的的图像进行匹配,速度提升11倍;(2)对于特征降维,使用最高效的Deep MDS++,对于1亿张192维的的图像进行匹配,速度提升6倍,且只有0.1%的精确度损失;(3)在加密域中进行图像搜索时,性能评价要求:准确率、延迟率、内存消耗;(4)实验性能:对于1亿张32维的的图像进行1:1匹配时,速度提升186倍,耗时10min,且2%的精确度损耗。
相关工作
隐私保护在生物特征中的应用


- 生物特征的隐私保护方法,主要有两个方向:(1)加密;(2)模式识别
- (1)视觉密码常用于保护指纹和人脸图像等生物特征数据。混淆数据也是一种密码形式,常用于指纹和虹膜识别。
- (2)模式识别可以替代密码,当前有生我特征和密钥结合的案例、基于神经网络和模板表示已经用于人脸识别等。
- 本文提出的方法HERS,具有很高的安全性和较小的损失。

- 隐私计算在计算视觉中的应用:(1)基于MPC的人脸识别;(2)基于OT的图像检索;(3)基于Paillier加密的人脸认证;(4)基于DP和FHE的视频监控等
- HERS采用降维和加密的方式,在加密域中高效精准的匹配。
密态计算向量举例

-
使用HE计算特征向量之间的距离。
-
汉明距离:应用于数据传输差错控制编码的距离度量方式,它表示两个(相同长度)字符串对应位不同的数量。对两个字符串进行异或运算,并统计结果为1的个数,那么这个数就是汉明距离。我们也可以将汉明距离理解为两个等长字符串之间将其中一个变为另外一个所需要作的最小替换次数。
-
余弦距离,也可以叫余弦相似度。 几何中夹角余弦可用来衡量两个向量方向的差异,机器学习中借用这一概念来衡量样本向量之间的差异。相比距离度量,余弦相似度更加注重两个向量在方向上的差异,而非距离或长度上。
n维空间中的余弦距离为:
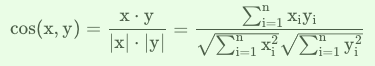
余弦取值范围为$[ − 1 , 1 ] $,求得两个向量的夹角,并得出夹角对应的余弦值,此余弦值就可以用来表示这两个向量的相似性。夹角越小,趋近于\(0\)度,余弦值越接近于\(1\),它们的方向更加吻合,则越相似;当两个向量的方向完全相反夹角余弦取最小值\(-1\);当余弦值为\(0\)时,两向量正交,夹角为90度,因此可以看出,余弦相似度与向量的幅值无关,只与向量的方向相关。
-
现有成果:(1)两个512维的人脸特征进行1:1比较,耗时2.5ms,占内存16KB;(2)对192维的指纹特征进行1:1比较,耗时1.25ms。

- 使用FHE针对1:1的匹配,效果还算可以,但对于1:m匹配时,时间和空间复杂度都很高,比如对于512维的加密图像特征进行1:100000000匹配,耗38h和9TB的内存。
压缩特征

- 这部分没看太懂,就是该方案使用DeepMDS用于压缩特征、
解决方法

- 为了提升加密域中搜索效率,有两种方法:(1)优化加密算法;(2)尽可能压缩维数,使得准确率损失降低。
- 在HERS中,聚合了这两种方法,下面分别介绍。
加密和未加密匹配
未加密
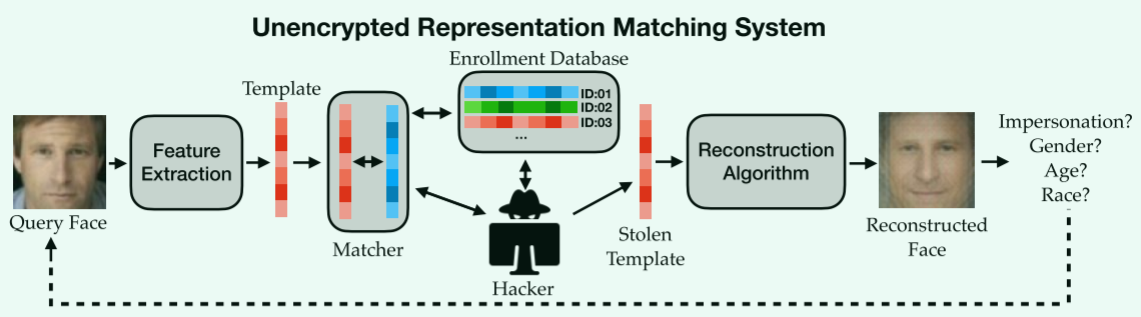
- 两个数据库:(1)注册数据库,存放全部数据;(2)匹配数据库,暂存匹配数据
- 流程:(1)注册,形成注册数据库;(2)匹配,人脸先提取特征,再和注册数据库一一比对
- 问题:(1)黑客获取未加密的注册数据库,可以发起模拟攻击,模拟数据库与匹配库交互;(2)就算注册数据库加密了,黑客可以获取匹配器,模拟与注册数据库交互。
加密
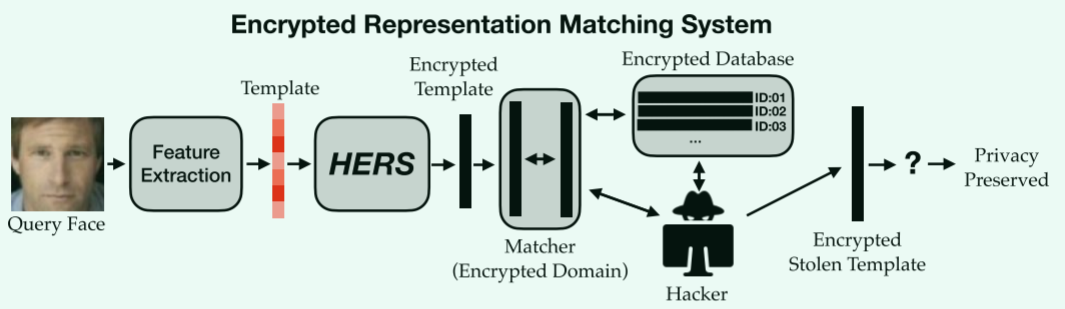
- 注册数据库加密
- 在密态下进行匹配


- 这里匹配的过程是,\(m\)条数据(数据库)\(P=[p_1,...,p_m]\in R^{d*m}\),匹配值\(q\in R^d\),结果是一个小数,表示相似度,使用欧几里得距离或者余弦相似度来计算,最重要的计算是\(r(P,q)=P^Tq\),矩阵乘向量的计算,即\(md\)次标量乘(scalar multiplications)和\(md\)次标量加法(scalar additions)。
- 这里的\(r(P,q)\)表示矩阵乘向量,\(f(P,pk)\)表示加密,\(g(f(P,pk),sk)\)表示解密
BFV方案

参数设置

- 本方案使用BFV加密方案,重新构造编码方式。
- BFV方案:
- 参数:\(\lambda\)是安全参数,\(w\)是基数,将\(q\)拆分为\(l=\left \lfloor log_wq \right \rfloor\)项
- 明文空间:\(R_t=Z_t[x]/\Phi_n(x)\),其中\(t\in Z\)是明文模数,\(\Phi_n(x)\)是最大级数为\(n-1\)的不可约多项式
- 密文空间:\(R_q=Z_q[x]/\Phi_n(x)\),其中\(q\in Z\)是密文模数
- 有三个密钥:
- \(pk\),是公钥
- \(sk\),是私钥
- \(evk\),是计算密钥,用于密文乘法
- 只要在密文计算时模数(多项式的系数)不超过\(q\),就可以正确解密。
密钥生成

- \(sk,pk=([-(a*sk+e)_q],a),evk=(evk^1,...,evk^l)\)
加密

- 明文放在了\(ct[0]\)上。
解密

- \(\frac{t}{q}\)远小于\(q\)
加法

- \(ot=ct_0+ct_1=(ct_0[0]+ct_1[0],ct_0[1]+ct_1[1])=\\ ([\Delta *m_0+pk[0]*u_0+e_{1,0}]_q+[\Delta *m_1+pk[0]*u_1+e_{1,1}]_q, [pk*u_0+e_{2,0}]_q+[pk*u_1+e_{2,1}]_q)=\\ ([\Delta *(m_0+m_1)+pk[0]*(u_0+u_1)+(e_{1,0}+e_{1,1}]_q,[pk*(u_0+u_1)+(e_{2,0}+e_{2,1})]_q)\)
乘法

- 第【5、6、7】步都是重线性化的过程
- \(c_2^{(i)}\)表示\(c_2\)的第\(i\)个元素
编码


-
BFV是对整数进行计算的,所以对于实数,需要编码为整数,进而在进行计算,转换精度为0.004,以基为\(w\)表示整数。
-
本文的工作之一就是利用SIMD技术设计高效的1:m的匹配,即将多个数通过CRT原理编码为同一个多项式。

- 【Secure face matching using fully homomorphic encryption-2018】中也使用的SIMD编码,是按列编码的,即将\(q\in Z^d\)编码为一个多项式,而本文是按行编码的,即将\(q\in Z^d\)编码为\(d\)个多项式。
- 对于查询项\(q\in Z^d\),编码为\(d\)个多项式,即\(g_i= {\textstyle \sum_{j=1}^{m}}q[i]x^{j-1},i\in \left \{ 1,...,d \right \}\),对于数据库\(P\in Z^{d*m}\),将每行\(P_i\in Z^m\)编码为的一个多项式,即\(h_i={\textstyle \sum_{j=1}^{m}}p_j[i]x^{j-1},i\in \left \{ 1,...,d \right \}\)。
- \(<P,q>=s={\textstyle \sum_{i=1}^{d}}g_i*h_i={\textstyle \sum_{j=1}^{n}}<q,p_j>x^{j-1}\),其中\(g_i*h_i\)就是标准的多项式乘法。
- 通过\(d\)次标准的多项式乘法可以求出\(m,(m<n)\)次内积,若\(m>n\)时,\(m\)个样本可以分为\(\left \lceil \frac{m}{n} \right \rceil\)个数据库(每\(n\)个为一个)。
这里\(n\)为什么出现在此?
方案
基本方案
方案包含两步:(1)注册;(2)检索
注册

- 客户端:
- 生成公私钥
- 选择一个样本(人脸图像)
- 提取特征(向量)
- 编码为一个明文多项式
- 加密为密文多项式,并将密文多项式连同样本的序号(metadata of the template,自己理解的)发给服务器
- 服务器:
- 将密文多项式添加到数据库中
服务器全程不知道明文,下面是具体协议:
- 有两点需注意:
- 这里考虑了数据库中样本数\(m\)大于多项式的次数(环的维数)\(n\)
- 还考虑了在线注册场景,即一次向密文库中注册一个密文特征

-
初始化:
- 参数设置:\(b_c\),系数比特长度;\(t\)明文模数;\(q\)密文模数;\(n\),环的维数
- 服务器初始化空的数据\(D_i\)和对应标签\(I\),数据库的序号是\(k,v\)
-
客户端:
- 密钥生成:\(pk,sk,evk\)
- \(q\in R^{d*m}\)是要注册的样本源,可以看成\(d\)个\(m\)维的特征向量
- 每\(m\)个(每行)编码为一个明文多项式\(m\),然后加密为密文多项式\(ct_i\),其中\(i\in\left \{ 1,...,d \right \}\)
- 增加数据库的索引:\(k=k+m\),这里不应该是\(k=k+d\)?
- 然后将密文多项式和索引$(\left { ct_1,...,ct_d \right },id) $发送给服务器
-
服务器:
- 这里先加密全零的数据\(r_i\)赋值给数据库
- 然后再将密文多项式\(ct_i\)添加到数据库\(D\)中(密文加),即更新数据库
检索

-
很意外的写错了,这里居然使用私钥加密?(也不是对称啊?)
-
客户端:
- 给定要检索的样本\(q\)
- 提取特征
- 编码为明文多项式(一个??不是\(d\)个么?)
- 加密为密文多项式,并将其发给服务器
-
服务器:
- 密态计算出相似度返回给客户端
-
客户端:
- 解密得到最相似对应的序号(index)
- 然后根据【】将序号返回给服务器
服务器全程无法得知请求查询的\(q\)和计算出的相似度,所以安全。

- 参数:\(q\in R^d\)是检索值,\(I\)是标签库,\(D\)是数据库,\(n\)是环的维数
- 客户端:
- 将\(q\in R^d\)编码为\(d\)个明文多项式
- 然后加密为\(d\)个密文多项式,并将其发送给服务器
- 服务器:
- 加密零项得到\(s\)
- 其中乘法和加法就相当于内积操作,计算出相似度\(S\),并发送给客户端
- 客户端:
- 解密得到\(r\),最后从\(R\)得到概率最大的,即\(R\)中的最大值
复杂度分析

-
方案的的复杂度主要在:全同态计算的消耗上。
-
对于密文计算(\(n\)次密文多项式),加法计算复杂度会增加\(O(n)\)倍,乘法计算复杂度会增加\(O(n^2)\)倍。
-
【Secure face matching using fully homomorphic encryption-2018】中主要计算是向量与向量的内积;对于SIMD技术,将\(d\)维向量编码为一个多项式;在该方案中,主要的计算是通过密文旋转来计算内积,而不是对单个元素计算,这就导致了复杂度与数据库大小\(M\)呈线性关系。
-
在HERS方案中,改变了SIMD编码,使得计算复杂度增加较慢,所以数据库可以更大。
- 上表是\(d\)维的加密搜索项和\(m\)大的数据库匹配的计算复杂度。
降维



- 维度越低,复杂度就越低,所以需要压缩降维,但同时保持精度。
- 降维的含义就是,将一个图像从【ambient space】变为【intrinsic space】
- 【intrinsic dimensionality】就是能维护信息特征的最小维数
- DeepMDS技术,是可以将图像特征的【ambient space】变为【intrinsic space】,但是该技术存在一些问题
- 所以使用DeepMDS++技术,由多个非线性层组成,被训练为将一个【ambient space】变为【intrinsic space】,且保持【pairwise
distances】,具体来讲,就是将一个在【ambient space】中的高维特征向量\(q\in R^d\)通过\(f(q,w)\),变为【intrinsic space】中的低维向量\(y=f(q,w)\),其中\(w\)是参数 - 后面的就看不懂了
实验
- DeepMDS++技术是在TensorFlow中实现的
- 加密搜索是在Seal库中实现的

- 这是可选取的数据集


- 这是提取图像特征向量的方法
效率


- 【Secure face matching using fully homomorphic encryption-2018】针对的是1:1的匹配,下面是和文本在不同维数的计算复杂度
- HERS是的数据库是可变的,可以并行处理
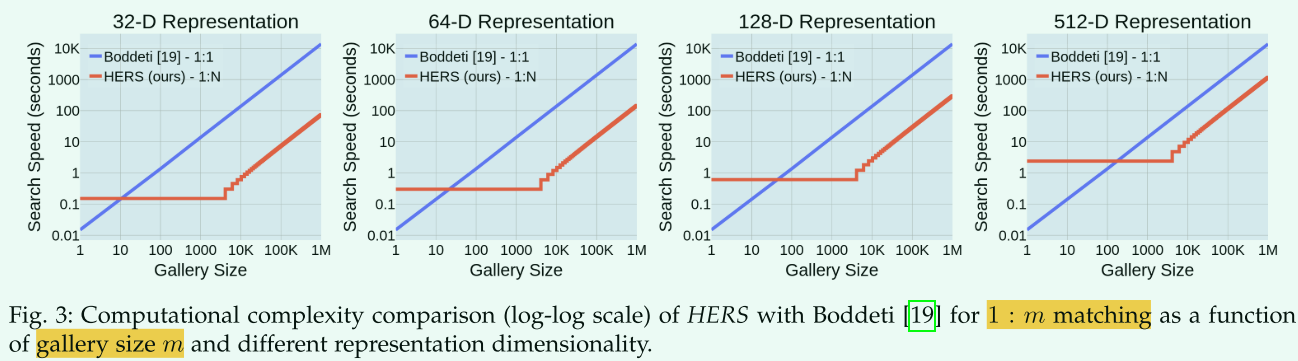
- 使用DeepMDS++技术可以将维度压缩四倍,性能损失为2.6%
- 对于一亿张32维的图像,可以在740s内匹配到;16维的图像,匹配时间可以缩减到370s,但精度损失严重。另外在客户端解密一亿个分数只需要不到1s
- 为了能降到16维,所以提出了两阶段加密搜索算法(two stage encrypted search)
- 第一步,通过匹配器获取相似top-K
- 第二步,重新排序,取第一个
这样就可以设置一个阈值。但还有一个缺点,需要对特征加密两次(一次用HERS编码后加密、一个是在【19】中编码后加密)
- 通过降低维度(牺牲精确度)和改进编码方案(牺牲内存)来获取较快的检索速度
安全性
- 半城实安全,即客户端在遵守协议的同时可以收集额外信息
- 方案的安全性依赖于BFV方案,即规约到RLWE问题
- 形成128bit的安全强度
- 即使攻击者得到了未加密的相似度(分数),也得不到对应的特征向量,即\(r=P^Tq\),需要知道\(P\)才能知道\(q\)
总结
-
替换FHE的方法:
- 使用部分同态,例如Paillier
- 使用MPC,即使用秘密分享来计算相似度
-
文本提出一个精确实用的HERS方案
-
效率:
- 加密矩阵向量积
- DeepMDS++用为降维
-
准确度:
- 精确计算
- DeepMDS++在压缩时,保持一定的精确度
-
效果:在加密域中对一亿张图搜索需10min,准确率为2%
疑问
- 什么是定长表示(Fixed-Length Representation)?
- 关于DeepMDS++如何降维没看懂?
- 关于两阶段加密搜索具体没看懂?


 浙公网安备 33010602011771号
浙公网安备 33010602011771号