优化算法总结

1、梯度下降法

给定一个目标函数f（x）和初始点x₀

△x_t = -▽f(x_t)

x_t+1 = x + η△x_t

停止条件：当 |△x_t| < ε时停止

三大问题：局部最小值、鞍点、停滞区。

1.1 局部最小值（极值）

1.2 停滞区

函数有一段很平的区域，这时梯度很小，权值就更新的特别慢。

1.3 鞍点

鞍点处梯度为0，但不是局部最大值也不是局部最小值。

鞍点坐在的位置在一个方向上式最大值，在另一个方向上是最小值。

二、带冲量的梯度下降法

给定一个目标函数f（x）和初始点x₀，初始动量v₀

△x_t = -▽f(x_t)

v_t+1 = γv_t + η△x_t

x_t+1 = x_t + v_t+1

停止标准：冲量小于一个值，或梯度小于一个值，或给定一个迭代次数

在梯度下降法的基础上，加上一个冲量的项，每次迭代乘一个衰减系数。

三、NAG（Nesterov accelerated gradient descent）

改进带冲量的梯度下降法。

给定一个目标函数f（x）和初始点x₀，初始动量v₀

△x_t = - ▽f( x_t +  γv_t )

v_t+1 = γv_t + η△x_t

x_t+1 = x_t + v_t+1

可以发现，求梯度的位置不在是当前位置的梯度，而是沿着当前冲量乘衰减系数前进一步之后所在的位置。

例如骑自行车下坡，原来是根据当前的坡度决定车怎么走，而现在是根据前方的坡度来决定车往哪儿拐。

四、牛顿法

1、牛顿-拉普森算法（NR newton-Raphson）

用来寻找实值方程的近似解。

给定方程f（x）= 0，初始点x₀

△x = - f(x_t) / f'(x_t)

x_t+1 = x_t + △x

停止：如果|f(x)| < ε

2、牛顿法求极值

给定f（x）和初始点x0

x_t+1 = x_t - f'(x_t)/f''(x_t)

停止：| f'(x_t) | < ε

若f(x+△x)是极小值点，将其泰勒展开到二阶：

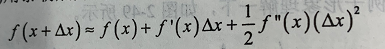
函数对称轴出就是极值，则：

牛顿法每次迭代，在所在的位置对要求解的函数做一次二次近似，然后直接用这个近似的最小值作为下一次迭代的位置。在高维下计算量有点大。

五、学习率衰减

前期使用叫大的学习率，后期使用较小的学习率。

lr = lr_base x γ^{| step/stepsize |}

基础学习率；

γ是小于1 的衰减系数；

step：当前迭代步数

stepsize：总共迭代次数

六、AdaGrad（adaptive gradient），每个变量都有自己的节奏

要优化的变量对于目标函数的依赖是不同的。对于某些变量，已经优化到了极小值附近，但是有的变量仍然在梯度很大的地方，这时候一个统一的全局学习率就会出现问题。如果学习率太小梯度很大的变量会收敛的很慢，学习率太大，梯度很小的变量会不稳定。

自适应学习率，基本思想是每个变量用不同的学习率，刚开始学习率比加大，随着优化过程的进行，对于已经下降很多的变量，则减缓学习率，对于没怎么下降的变量，仍然保持一个叫大的学习率。总的来说是根据历史学习率积累量来决定当前学习率减小的程度。

如下图，垂直方向梯度变化快，水平方向梯度变化慢，一般的梯度下降法，梯度大的时候会沿着垂直方向，梯度小的时候再沿着水平方向，而AdaGrad走的是那个弧形的路线，更快到达A点。

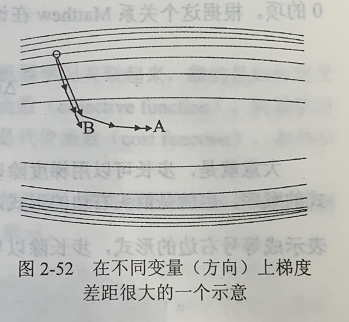
AdaGrad适合样本稀疏的问题，因为稀疏的样本下，每次梯度的方向可能会有很大差异。

需要手工指定初始学习率。

七、AdaDelta

对AdaGrad做出的改进：

（1）累计梯度信息从全部历史梯度改为当前时间向前一个窗口期内的积累；

（2）不用指定学习率，学习率 = 步长/导数，属于相同量纲。

量纲：单位具有实际的物理意义，而量纲则不一定。.比如说m·s（米乘以秒），这种就是量纲，这个的用处只是为了考察某些物理公式是否具有相同量纲从而确定其正确性。

八、其他

RMSProp、Adam、Adamax

一般情况下都是使用带冲量的梯度下降法，效果不好的话使用自适应法，但是优化到后期，自适应法例如AdaGrad、RMSProp一直震动，不如带冲量的梯度下降法好。