《浅谈棋盘模型在计数问题中的应用》 - 学习笔记

Itst Orz

以下的 \(n\) 一般表示棋盘的大小为 \(n\times n\) 。 \(B_n=\{(i,j)\mid 1\le i,j\le n\}\) 。

对于一个棋盘 \(S\) ，定义棋盘数 \(r_k(S)\) 表示在 \(S\) 里面放 \(k\) 个棋子的方案数，定义 \(h_{k,n}(S)\) 表示所有 \(R_n(B_n)\) （相当于所有排列）中，恰好有 \(k\) 个棋子在 \(S\) 里面的方案数。

4 基础定理

4.1 棋盘数与命中数的关系

显然有

\[r_k(S)(n-k)!=\sum_i {i\choose k}h_{i,n}(S) \]

然后做一番变形，可以得到

\[\sum_k h_{k,n}(S)(x+1)^k=\sum r_k(S)(n-k)!x^k \]

所以命中数可以转化为棋盘数。

4.3 分离定理

同行同列的点连边，那么不同的连通块可以分开计数，然后棋盘多项式就是乘在一起。

5 禁区排列问题

错排问题：令 \(S=\{(i,i)\mid 1\le i\le n\}\) ，那么要求 \(h_{0,n}(S)\) 。用上面那个式子反演一下即可得到 \(h_{0,n}(S)=\sum_k (-1)^k (n-k)!r_k(S)\) ，而显然 \(r_{k}(S)={n\choose k}\) 。

夫妻分座问题：给定 \(n\) 和两个排列 \(p,q\) ，对每个 \(k\) 求有多少个排列 \(\pi\) 使得 \(\sum [\pi_i=p_i\or \pi_i=q_i]=k\) 。

也就是求命中数，可以转化为求棋盘数。这里的棋盘非常稀疏，可以把每一列看做连接两个点的边，然后对每个环计数。

6 Ferrers 棋盘的棋盘多项式

Ferrers 棋盘是满足 \(S=\{(i,k)\mid 1\le k\le a_i\}\) 且 \(a\) 单调不降的棋盘，记为 \(F(a_1,\cdots,a_n)\) 。

6.1 下降幂棋盘多项式分解定理

显然 \(r_n(S)\) 是容易计算的。对于没有放满的情况我们可以干一些奇怪的事情，在下面多加 \(x\) 行，然后把没有放的列强制在下面放满。

（这种加 \(x\) 行然后强制放满的思路在后面还会用到。）

加了 \(x\) 行之后，放满的方案数是

\[\sum_k r_k(S)x^{\underline{n-k}}=\prod (x+a_k-(k-1)) \]

因为对于所有足够大的非负整数 \(x\) 都成立，于是就得到系数对应相等。

普通多项式转下降幂多项式并不是很好做，但是可以在分治 NTT 计算右边的时候直接维护下降幂多项式。

黑白分离，然后旋转 45° ，然后交换行列边数 Ferrers 棋盘，然后发现形式非常好看，可以直接计算出右边的点值，然后卷积得到了下降幂多项式。

6.2 阶梯棋盘与斯特林数

定义阶梯棋盘为满足 \(a_i=i-1\) 的 Ferrers 棋盘，记为 \(St_n\) 。

用上面那个定理，直接得到

\[\sum_k r_k(St_n)x^\underline{n-k}=x^n \]

所以有 \(r_{n-k}(St_n)={n\brace k}\) 。另外也可以无脑 DP ，然后发现转移式和初始值与斯特林数完全一样。

还可以再整个阴间双射：把 \(n\) 个数分成 \(k\) 个无序集合，在每个集合中把元素排序得到 \(\{a_1,\cdots,a_p\}\) ，那么对于 \(1<i\le p\) 放棋子 \((a_i,a_{i-1})\) 。

另外还可以把圆排列也整个活。

设 \(f_k(S)\) 表示在棋盘 \(S\) 上放 \(k\) 棋子，且任意两个棋子不同列的方案数。也就是把不同行的限制删掉了。

对于 Ferrers 棋盘，仍然用加上 \(x\) 行的方法，得到

\[\sum_k f_{n-k}(S)x^{k}=\prod (x+a_i) \]

所以如果 \(a_i=i-1\) 则有 \(f_{n-k}(St_n)={n\brack k}\) 。

然后也可以整一个双射，不过不是很阴间。对于一行，如果选择放 \(x\) （也就是不放），那就单独开一个圆排列；否则如果放在了 \((i,k)\) 则说明把 \(i\) 插入到 \(k\) 后面。

斯特林数有反演公式

\[\sum_{k} {y\brace k}{k\brack x}(-1)^{k-x}=[x=y] \]

而上面给出了第一类和第二类斯特林数在棋盘中的组合意义，所以尝试用这个组合意义来证明反演公式。

构造了一个神奇双射，然后一波操作发现可以给 \(x,y\) 都减一且答案不变，然后到 \(x=0\) 就显然为 0 了。不想写了。

6.3 棋盘等价类

称两个棋盘等价当且仅当每个棋盘数都相等，即棋盘多项式相等。

对于 Ferrers 棋盘 \(S=F(a_1,\cdots,a_n)\) ，在前面补 0 使得 \(n=|S|+1\) 。现在定义可重集 \(B_S=\{b_{S,1}=a'_1,b_{S,2}=a'_2-1,\cdots,b_{S,|S|+1}=a'_{|S|+1}-|S|\}\) ，那么两个 Ferrers 棋盘等价当且仅当它们的 \(B\) 相等。

由下降幂棋盘多项式分解定理，这很显然。

容易发现 \(b\) 全都是非正的。设 \(k=-\min_i b_{S,i}\) ，那么可重集就可以被表示成 \(0^{c_0}(-1)^{c_1}\cdots(-k)^{c_k}\) 。因为相邻两个 \(b\) 最多减一，所以 \(c\) 全部为正。

另外 \(b\) 要满足什么限制才能对应回一个 Ferrers 棋盘？一个是里面的元素非负，另一个是 \(b_{i+1}\ge b_i-1\) ，最后是 \(\sum_i b_i=|B|-1-{|B|(|B|-1)\over 2}\) 。

对任意一个非空 Ferrers 棋盘 \(S\) ，存在恰好一个没有空列的严格增 Ferrers 棋盘与之等价。不难通过 \(c\) 构造出这么一个棋盘。

最后，对于一个合法的可重集 \(0^{c_0}(-1)^{c_1}\cdots(-k)^{c_k}\) ，有几个 Ferrers 棋盘与之对应？

唯一需要考虑的限制是 \(b_{i+1}\ge b_i-1\) 。从大到小加入数，加入 \(x\) 时每一段 \(x\) 的前面一个位置必须是 \(x+1\) ，所以容易得到方案数

\[\prod_{i=1}^k {c_i+c_{i-1}-1\choose c_{i-1}-1} \]

6.4 分解定理的变体

定义两个与棋盘数类似但不同的量。

定义 \(m\) 阶 \(k\)-棋盘数：对于棋盘 \(S\) 和正整数 \(m\) ，从下往上每 \(m\) 行分成一个行组，那么定义一个合法的放棋子方案为任意两个棋子不在同一列且不在同一行组的方案。设放 \(k\) 个棋子的方案数为 \(r_{m,k}(S)\) 。

其中 \(x^\underline{n,m}=\prod_{i=0}^{n-1}(x-im)\) 。

这个公式也不难理解，就是加上 \(x\) 行，然后同一组的零散部分统一分配。我们强制 \(m|x\) 且足够大。

另外一个定义感觉挺牵强的，不管。

显然 \(\alpha\) 没啥用，可以假装 \(\alpha=-1\) 。如果 \(a\) 单调不降那么就是算棋盘多项式，但可惜并不是。

然而我们有取模，而给一个位置加上若干个 \(mod\) 并不会影响答案，所以可以调整之后再做。

再注意到求答案的式子中给一个位置减去若干个 \(mod\) 也不会影响答案，所以其实什么都不用做。

由于干这两样事情与 \(mod\) 是啥无关，所以其实就是正确答案。

综上，只需要假装 \(a\) 是单调不降的，用原来的方法算棋盘多项式即可。

7 排列降低计数

显然排列 \(\text{Sym}(n)\) 和 \(R_n(B_n)\) 之间可以建立双射。但是降低对与相邻两个位置有关，所以不是很好计数。

下面是一个牛逼的变换，把降低与超过建立了关系。

7.1 Foata 第一基本变换

其实是个比较直观的变换，可以把超过变成降低。

连边 \(i\to p_i\) ，然后尝试构造一个新的排列，使得 \(p_i\) 恰好在 \(i\) 的前面，这样就转化为降低了。

当然显然不可能使得所有都成立，但是这个变换使得该成立的都成立了。

逆变换则是把前缀最大值取出来，然后乱搞。

于是我们有

超过计数也可以转化为降低计数，所以容易发现

\[\left\langle\!{\begin{matrix}n\\k\end{matrix}}\!\right\rangle=h_{k,n}(St_n) \]

而 \(h\) 可以再容斥一下变成 \(r\) ，于是就得到了式子

\[\left\langle\!\begin{matrix} n \\ k \end{matrix}\!\right\rangle=\sum_{i=k}^{n}(-1)^{i-k}{i\choose k}{n\brace n-i}(n-i) ! \]

7.2 k-超过数计数

由于 k-超过数 对应的棋盘满足任意两个位置不同行同列，所以直接有

\[r_i(S)={n-k\choose i} \]

然后直接容斥，得到

\[P_{n,k,p}=\sum_i (-1)^{i-p}{i\choose p}{n-k\choose i}(n-i)! \]

另外，考虑这样一个增量法：从 \(\pi\in \text{Sym}(n-1)\) 推到 \(\pi'\) ，可以先把 \(n\) 放在最后，然后在前面选择一个 \(i\) ，交换 \(\pi_i\) 和 \(\pi_n\) 。

对于 \(0\le k<n,p\ge 1\) ， \(P_{n,k,p}\) 满足一个丑陋的递推式

\[P_{n, k, p}=P_{n-1, k, p-1}+(p+1) P_{n-1, k, p+1}+(n-p-1) P_{n-1, k, p} \]

在 \(0\le k<n,p=0\) 时则有 \(P_{n,k,0}=(n-1)P_{n-1,k,0}+(n-k-1)P_{n-2,k,0}\) 。前者是随便找一个位置换过去，而后者是 \(P_{n-1,k,1}\) 。把 \(P_{n-1,k,1}\) 命中的格子所在的行列删掉，就得到了 \(P_{n-2,k,0}\) ，而从后者推到前者则有 \(n-k-1\) 中方法。

另外，直接考虑最后 \(k\) 个位置放了什么，可以得到

\[P_{n, k, 0}=k ! \sum_{r=0}^{k}\left(\begin{array}{l} k \\ r \end{array}\right)\left(\begin{array}{l} n-k \\ k-r \end{array}\right) P_{n-k, k-r, 0}\ \ \ \ 0\le k<n \]

另外，显然有

\[P_{n,k,s}={n-k\choose s}P_{n-s,k,0} \]

7.3 X-Y 降低计数

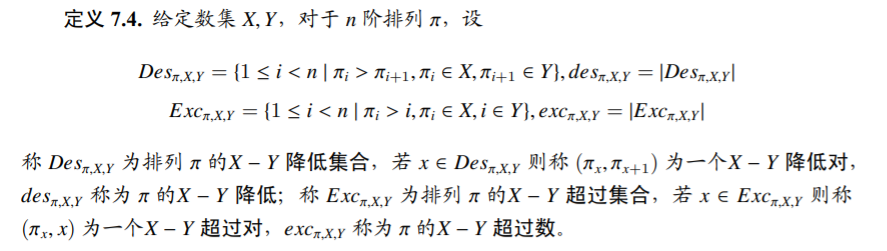
显然这两者也可以换来换去。

X-Y 超过数很容易转化到棋盘上，并且就是 \(St_n\) 删掉一些行列，一番操作也可以得到 Ferrers 棋盘。

然后好像没有太多内容了。

8 Ferrers 棋盘的排列逆序对计数

8.1 k-棋盘数的 q-analogue 形式

对于一个排列，把每一个点的右边和下面染黑，那么顺序对的个数就是未被染黑的格子数。容易找到它们之间的一一对应关系。

所以逆序对也很容易确定。

对于棋盘 \(S\) 和一个方案 \(T\subseteq S\) ，定义 \(val_S(T)\) 为对 \(T\) 染色之后 \(S\) 中还没有被标记的格子个数，定义 \(C_S(T)\) 为这样的格子的集合。

8.2 q-analogue 形式下的分解定理

（然而这里并不是关于 \(x\) 的多项式，所以不是很好证。）

但是 \(x\) 是自然数的时候比较简单。还是用一样的方法，在下面多加 \(x\) 行。然后这个式子挺显然的。

特别地，有

\[\left[r_{n}(S)\right]_{q}=\prod_{i=1}^{n}\left[a_{i}-i+1\right]_{q} \]

9 Ferrers 棋盘的排列环数计数

数环的个数。也可能可以夹带私货，把链也一块包括。

然而环和棋盘看起来毫无关系……

9.2 有向图的覆盖多项式

显然一个棋盘可以和一个邻接矩阵对应，也就可以对应到一个可以有自环、无重边的有向图。

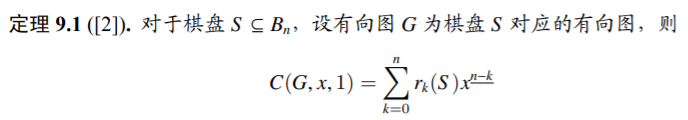
这个挺显然的。

因为行列保留的是一样的集合，所以把它转成有向图之后就是要求每个导出子图的覆盖多项式 \(C(G,x,1)\) 。

把一个点集组成环和组成链的方案数都先求出来，然后拼在一起求几何幂级数的 \(\exp\) 。但是我们还关心链的个数，所以直接做是需要对二元函数做 \(\exp\) 的，比较爆炸。可以算点值，最后插值，消掉链的个数这一维。

9.3 Ferrers 棋盘覆盖多项式分解定理

像之前一样，很容易把一个放车的方案对应到一个编号范围为 \(\mathbb{Z}\) 的有向图上，并且这个有向图只有环和链。

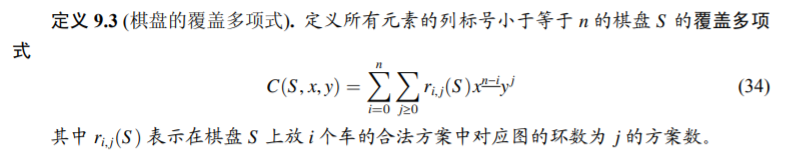
注意每一列的高度可能很高。但是这不重要，因为如果连到了大于 \(n\) 的位置就一定不会再有出边了。

可以看做每个环带一个 \(y\) 的权值，并且在棋盘下面加阴间 \(x\) 个编号为负数的行，然后强制拿满。

用类似 UOJ597 的做法，可以得到

\[C(S, x, y)=\prod_{1 \leq i \leq n} (x+a_i-(i-1)+[a_i\ge i](y-1)) \]

9.4 分解定理在减 Ferrers 棋盘上的拓展

上面的正确性依赖于：对于 \(i<j\) ，如果存在边 \((i,j)\) ，那么一定存在边 \((j,i)\) 。但在减 Ferrers 棋盘上不存在这个性质。

但是论文告诉我们，可以强行把棋盘变成竖直型减 Ferrers 棋盘，使得覆盖多项式不变，且两个棋盘的环和链之间还存在一一对应关系。

不是很想看了，跑了跑了。也可以去看 UOJ597 。