匈牙利算法

匈牙利算法其实就是一种递归，是由匈牙利数学家提出，该算法的核心就是寻找增广路经，它是一种用增广路径求二分图最大匹配的算法。
　其时间复杂度为O(v*e),v为左边的个数，e为右边的个数。

 

这是一个二分图，现在求这个图的最大匹配。

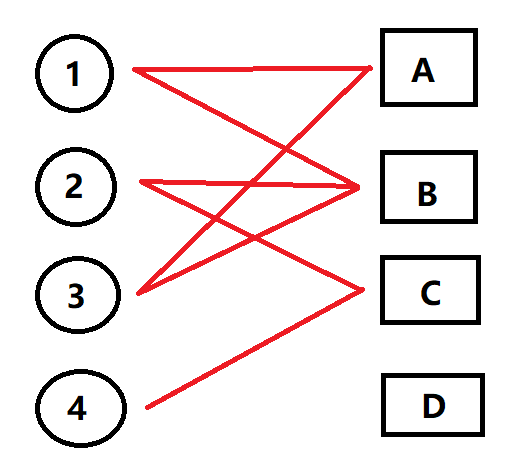
（1）

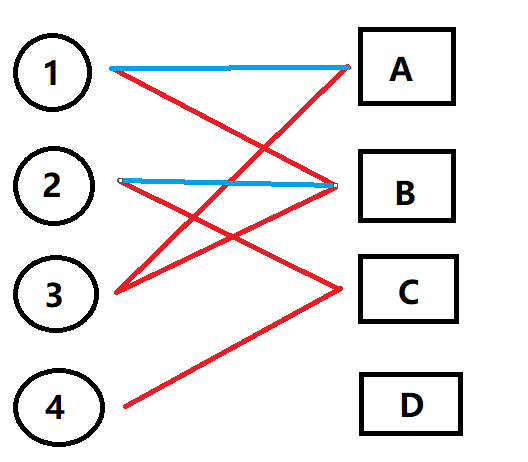
最开始的匹配会得到

　　1->A;  2->B;

（2）

当对3进行匹配时，会发现3所对应的A和B 都已经被匹配完毕。此时为了大局着想，1和2必须为3让位。

首先1把A让给3，即 3->A;

此时会发现1还有可以用来对应的，于是2把B让位给1，即1->B;

然后2呢也会有一个与其对应的字母C，所以3->C;

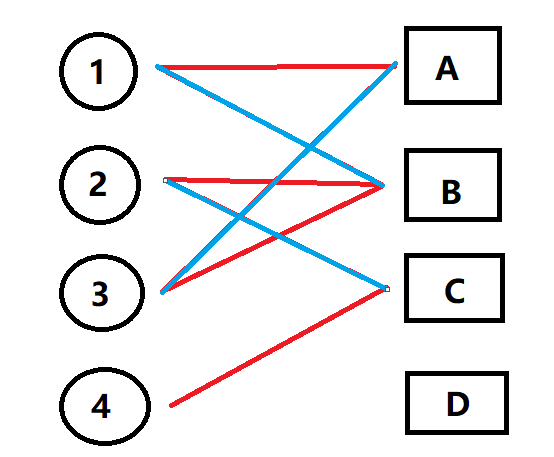
（3）

此时再来看4这个数字，由于他只能跟C进行匹配，所以假设4->C;

那么1，2，3就没有足够的字母来与其对应，所以4并没有能找到预期匹配的项。

所以这个二分匹配图的最大匹配就为3

 

算法实现：

//首先要进行初始化，将可以进行匹配的记录下来 
void init()
{
    for(int i=0;i<n;i++)
    {
        scanf("%d %d",&a,&b);
        g[a][b]=1;//a和b是可以进行匹配的 
    } 
}

然后就是对每个的数字进行遍历，寻找最大匹配的数量

for(int i=1;i<=4;i++)
{
    memset(mark,0,sizeof(mark));
    //将字母进行初始化，也就是所有的字母没有被选过
    if(find(i))
    {
        ans++;
    } 
} 
//输出结果 

其中该算法的核心就是进行多次匹配的时候的“让”了。

int find(int x)
{
    for(int i=1;i<=4;i++)
    {
        if(g[x][i]==1&&mark[i]==0)
        {
            mark[i]=1;
            //如果字母没有被匹配，而且可以通过更改之前匹配的项
            //让其可以得到一个对应的字母，那么就返回1 
            if(zm[i]==0||find(zm[i]))
            {
                zm[i]=x;
                return 1;
            }
        }
    }
    return 0;
}

 

3个重要结论：

最小点覆盖数：最小覆盖要求用最少的点（X集合或Y集合的都行）让每条边都至少就、和其中一个点关联。可以证明：最少的点（覆盖数）= 最大匹配数

最小路径覆盖=| N | - 最大匹配数

用尽量少的不相交简单路径覆盖  有向无环图 G  的所有节点。解决此类问题可以建立一个二分图模型。把所有的顶点i拆分成两个： X结点集中的i和Y结点集中的 i ，如果有边i->j ，则在二分图中引入边 i -> j ，设二分图最大匹配数为 m ,则结果就是 n-m

二分图最大独立集 = 顶点数 - 二分图最大匹配

在 N 个点的图G 中选出 m 个点，使这个 m 个点两两之间没有边，求m的最大值

如果图G 满足二分图条件，则可以用二分图匹配来做，最大独立集点数 = N - 最大匹配数