Java面经之排序算法

排序算法

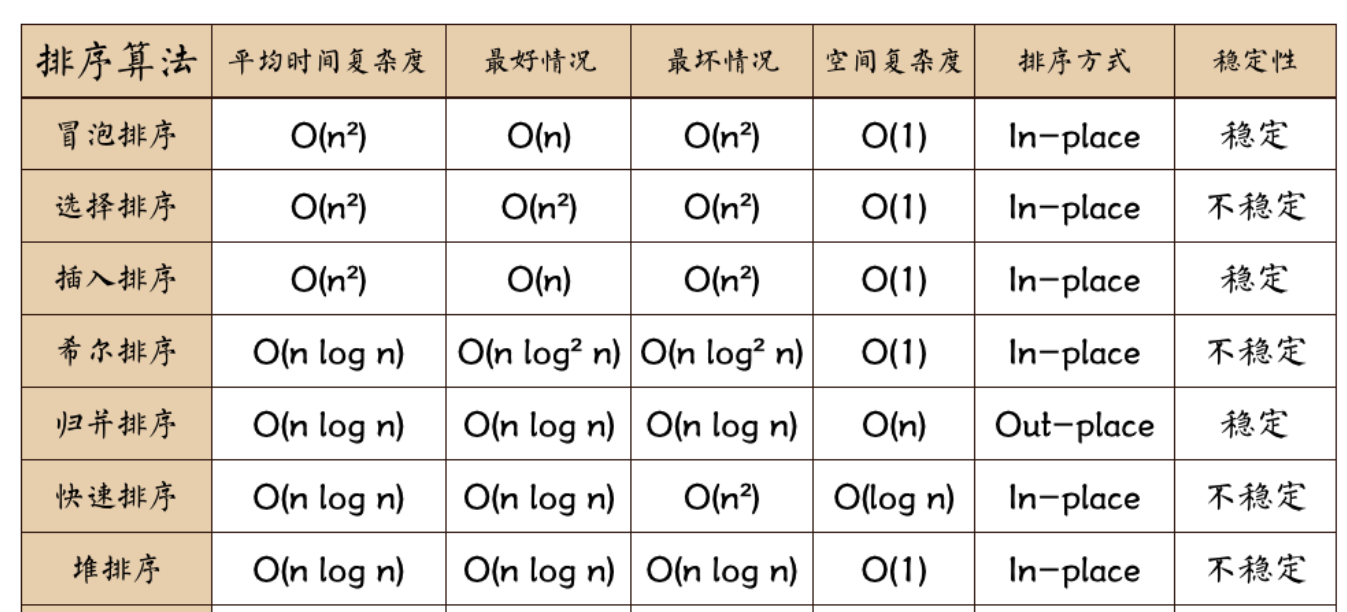
一、冒泡排序

public static int bubbleSort(int[] array) {
    if (array.length == 0) 
        return array;
    for (int i = 0; i < array.length; i++)
        for(int j = 0; j < array.length - 1 - i; j++) {
            if (array[j + 1] < array[j]) {
                int tmp = array[j];
                array[j] = array[j + 1];
                array[j + 1] = tmp;
            }
        }
    return array;
}

二、选择排序

public static int selectionSort(int[] array) {
    if (array.length == 0)
        return array;
   	for (int i = 0; i < array.length; i++) {
        int minIndex = i;
        for (int j = i; j < array.length; j++) {
            if(array[j] < array[minIndex])
                minIndex = j;
        }
        int tmp = array[i];
        array[i] = array[minIndex];
        array[minIndex] = tmp;
    }
}

三、插入排序

public static int[] insertionSort(int[] array) {
   if (array.length == 0)
       return array;
   int current;
   for (int i = 0; i < array.length - 1; i++) {
       current = array[i + 1];
       int preIndex = i;
       while (preIndex >= 0 && current < array[preIndex]) {
           array[preIndex + 1] = array[preIndex];
           preIndex--;
       }
       array[preIndex + 1] = current;
   }
   return array;
}

四、快速排序

int Partion(ElemType A[], int low, int high){
	ElemType pivot=A[low];
	while(low<high){
		while(low<high&&A[high]>=pivot)
			high--;
		A[low]=A[high];
		while(low<high&&A[low]<=pivot)
			low++;
		A[high]=A[low];
	}
	A[low]=pivot;
	return low;
}

void QuickSort(ElemType A[], int low, int high){
	if(low<high){
		int pivotpos=Partion(A,low,high);
		QuickSort(A,low,pivotpos-1);
		QuickSort(A,pivotpos+1,high);
	}
}

五、堆排序

每个结点的值都大于其左孩子和右孩子结点的值，称之为大根堆；每个结点的值都小于其左孩子和右孩子结点的值，称之为小根堆。

大根堆：arr(i)>arr(2i+1) && arr(i)>arr(2i+2)

小根堆：arr(i)<arr(2i+1) && arr(i)<arr(2i+2)

void BuildMaxHeap(ElemType A[], int len){
	for(int i=len/2;i>0;i--)
		AdjustDown(A,i,len);
}
void AdjustDown(ElemType A[], int k, int len){
	A[0]=A[k];
	for(int i=2*k;i<=len;i*=2){
		if(i<len&&A[i]<A[i+1])
			i++;
		if(A[0]>=A[i])
			break;
		else{
			A[k]=A[i];
			k=i;
		}
	}
	A[k]=A[0];
}
void HeapSort(ElemType A[], int len){
	BuildMaxHeap(A,len);
	for(int i=len;i>1;i--){
		swap(A[i],A[1]);
		AdjustDown(A,1,i-1);
	}
}

六、归并排序

public static int[] MergeSort(int[] array) {
    if (array.length < 2) return array;
    int mid = array.length / 2;
    int[] left = Arrays.copyOfRange(array, 0, mid);
    int[] right = Arrays.copyOfRange(array, mid, array.length);
    return merge(MergeSort(left), MergeSort(right));
}

public static int[] merge(int[] left, int[] right) {
    int[] result = new int[left.length + right.length];
    for (int index = 0, i = 0, j = 0; index < result.length; index++) {
        if (i >= left.length)
            result[index] = right[j++];
        else if (j >= right.length)
            result[index] = left[i++];
        else if (left[i] > right[j])
            result[index] = right[j++];
        else
            result[index] = left[i++];
    }
    return result;
}