神经网络优化篇：详解归一化网络的激活函数（Normalizing activations in a network）

归一化网络的激活函数

在深度学习兴起后，最重要的一个思想是它的一种算法，叫做Batch归一化，由Sergey loffe和Christian Szegedy两位研究者创造。Batch归一化会使的参数搜索问题变得很容易，使神经网络对超参数的选择更加稳定，超参数的范围会更加庞大，工作效果也很好，也会是的训练更加容易，甚至是深层网络。让来看看Batch归一化是怎么起作用的吧。

当训练一个模型，比如logistic回归时，也许会记得，归一化输入特征可以加快学习过程。计算了平均值，从训练集中减去平均值，计算了方差，接着根据方差归一化的数据集，在之前了解到的，这是如何把学习问题的轮廓，从很长的东西，变成更圆的东西，更易于算法优化。所以这是有效的，对logistic回归和神经网络的归一化输入特征值而言。

那么更深的模型呢？不仅输入了特征值\(x\)，而且这层有激活值\(a^{[1]}\)，这层有激活值\(a^{[2]}\)等等。如果想训练这些参数，比如\(w^{[3]}\)，\(b^{[3]}\)，那归一化\(a^{[2]}\)的平均值和方差岂不是很好？以便使\(w^{[3]}\)，\(b^{[3]}\)的训练更有效率。在logistic回归的例子中，看到了如何归一化\(x_{1}\)，\(x_{2}\)，\(x_{3}\)，会帮助更有效的训练\(w\)和\(b\)。

所以问题来了，对任何一个隐藏层而言，能否归一化\(a\)值，在此例中，比如说\(a^{[2]}\)的值，但可以是任何隐藏层的，以更快的速度训练\(w^{[3]}\)，\(b^{[3]}\)，因为\(a^{[2]}\)是下一层的输入值，所以就会影响\(w^{[3]}\)，\(b^{[3]}\)的训练。简单来说，这就是Batch归一化的作用。尽管严格来说，真正归一化的不是\(a^{[2]}\)，而是\(z^{[2]}\)，深度学习文献中有一些争论，关于在激活函数之前是否应该将值\(z^{[2]}\)归一化，或是否应该在应用激活函数\(a^{[2]}\)后再规范值。实践中，经常做的是归一化\(z^{[2]}\)，所以这就是介绍的版本，推荐其为默认选择，那下面就是Batch归一化的使用方法。

在神经网络中，已知一些中间值，假设有一些隐藏单元值，从\(z^{(1)}\)到\(z^{(m)}\)，这些来源于隐藏层，所以这样写会更准确，即\(z^{[l](i)}\)为隐藏层，\(i\)从1到\(m\)，但这样书写，要省略\(l\)及方括号，以便简化这一行的符号。所以已知这些值，如下，要计算平均值，强调一下，所有这些都是针对\(l\)层，但省略\(l\)及方括号，然后用正如常用的那个公式计算方差，接着，会取每个\(z^{(i)}\)值，使其规范化，方法如下，减去均值再除以标准偏差，为了使数值稳定，通常将\(\varepsilon\)作为分母，以防\(σ=0\)的情况。

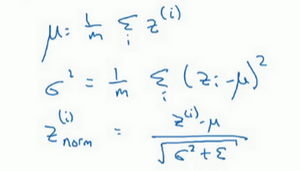
所以现在已把这些\(z\)值标准化，化为含平均值0和标准单位方差，所以\(z\)的每一个分量都含有平均值0和方差1，但不想让隐藏单元总是含有平均值0和方差1，也许隐藏单元有了不同的分布会有意义，所以所要做的就是计算，称之为\({\tilde{z}}^{(i)}\)，\({\tilde{z}}^{(i)}= \gamma z_{\text{norm}}^{(i)} +\beta\)，这里\(\gamma\)和\(\beta\)是模型的学习参数，所以使用梯度下降或一些其它类似梯度下降的算法，比如Momentum或者Nesterov，Adam，会更新\(\gamma\)和\(\beta\)，正如更新神经网络的权重一样。

请注意\(\gamma\)和\(\beta\)的作用是，可以随意设置\({\tilde{z}}^{(i)}\)的平均值，事实上，如果\(\gamma= \sqrt{\sigma^{2} +\varepsilon}\)，如果\(\gamma\)等于这个分母项（\(z_{\text{norm}}^{(i)} = \frac{z^{(i)} -\mu}{\sqrt{\sigma^{2} +\varepsilon}}\)中的分母），\(\beta\)等于\(\mu\)，这里的这个值是\(z_{\text{norm}}^{(i)}= \frac{z^{(i)} - \mu}{\sqrt{\sigma^{2} + \varepsilon}}\)中的\(\mu\)，那么\(\gamma z_{\text{norm}}^{(i)} +\beta\)的作用在于，它会精确转化这个方程，如果这些成立（\(\gamma =\sqrt{\sigma^{2} + \varepsilon},\beta =\mu\)），那么\({\tilde{z}}^{(i)} = z^{(i)}\)。

通过对\(\gamma\)和\(\beta\)合理设定，规范化过程，即这四个等式，从根本来说，只是计算恒等函数，通过赋予\(\gamma\)和\(\beta\)其它值，可以使构造含其它平均值和方差的隐藏单元值。

所以，在网络匹配这个单元的方式，之前可能是用\(z^{(1)}\)，\(z^{(2)}\)等等，现在则会用\({\tilde{z}}^{(i)}\)取代\(z^{(i)}\)，方便神经网络中的后续计算。如果想放回\([l]\)，以清楚的表明它位于哪层，可以把它放这。

所以希望学到的是，归一化输入特征\(X\)是怎样有助于神经网络中的学习，Batch归一化的作用是它适用的归一化过程，不只是输入层，甚至同样适用于神经网络中的深度隐藏层。应用Batch归一化了一些隐藏单元值中的平均值和方差，不过训练输入和这些隐藏单元值的一个区别是，也许不想隐藏单元值必须是平均值0和方差1。

比如，如果有sigmoid激活函数，不想让的值总是全部集中在这里，想使它们有更大的方差，或不是0的平均值，以便更好的利用非线性的sigmoid函数，而不是使所有的值都集中于这个线性版本中，这就是为什么有了\(\gamma\)和\(\beta\)两个参数后，可以确保所有的\(z^{(i)}\)值可以是想赋予的任意值，或者它的作用是保证隐藏的单元已使均值和方差标准化。那里，均值和方差由两参数控制，即\(\gamma\)和\(\beta\)，学习算法可以设置为任何值，所以它真正的作用是，使隐藏单元值的均值和方差标准化，即\(z^{(i)}\)有固定的均值和方差，均值和方差可以是0和1，也可以是其它值，它是由\(\gamma\)和\(\beta\)两参数控制的。