笛卡尔树

定义

笛卡尔树是一种二叉树，每一个结点由一个键值二元组 \((k,w)\) 构成。要求 \(k\) 满足二叉搜索树的性质，而 \(w\) 满足堆的性质。一个有趣的事实是，如果笛卡尔树的 \(k,w\) 键值确定，且 \(k\) 互不相同，\(w\) 互不相同，那么这个笛卡尔树的结构是唯一的。

性质

满足二叉搜索树和堆的性质，即 \(ls_k < i_k < rs_k\) 且 \(i_w < ls_w ≤ rs_w\)

建树

对于二元组 \((k,w)\) , 首先要满足 \(k\) 单调，若以数组下标 \(i\) 为 \(k\) ，则无需排序
for example
  为满足小根堆，则单调栈应维护单调递增的序列。why?

如图

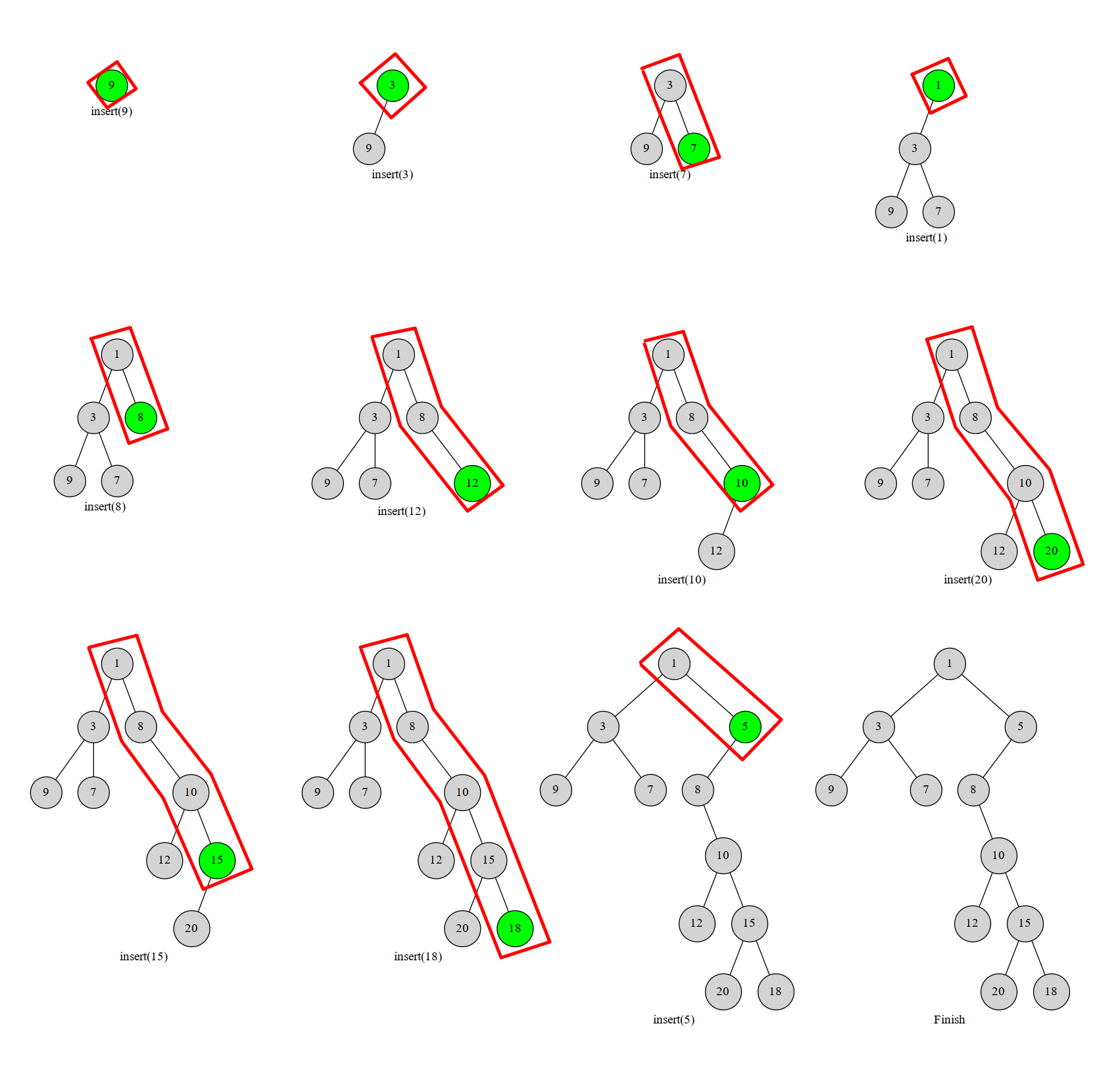
我们考虑将元素按照键值 \(k\) 排序。然后一个一个插入到当前的笛卡尔树中。那么每次我们插入的元素必然在这个树的右链（右链：即从根结点一直往右子树走，经过的结点形成的链）的末端。于是我们执行这样一个过程，从下往上比较右链结点与当前结点 \(u\) 的 \(w\)，如果找到了一个右链上的结点 \(x\) 满足 \(x_w<u_w\)，就把 \(u\) 接到 \(x\) 的右儿子上，而 \(x\) 原本的右子树就变成 \(u\) 的左子树。

对于排序好的 \(k\) , 下标已经单调递增了，所以新插入的点只能是已前面点的右儿子、前面点只能是它的左儿子

用单调栈维护一个权值单调递增的下标序列，这样踢出去的都是权值小的，因为单调栈求出的是 \(NGE\) 解，即第一个比元素大的值
维护一个右子树链的栈, 进行以下操作:

1、插入一个新节点 \(p\)

2、如果栈顶元素 \(u\) 的值大于 \(p\), 弹出\(u\), 并将其设为 \(p\) 的左儿子，否则, \(p\) 为 \(u\) 的右儿子.

3、最后, 栈顶元素即为树的根.

代码使用数组模拟栈，因为一个元素进出只有一次，故为 \(O(n)\)

模板

// Problem: P5854 【模板】笛卡尔树
// URL: https://www.luogu.com.cn/problem/P5854
// 解绑的cin都过不去，所以说这个题要过的话需要加Fast I/O
#include<bits/stdc++.h>
const int maxn = 1e7+100;
using namespace std;
int n,a[maxn],ls[maxn],rs[maxn],s[maxn];
signed main(){
    scanf("%d",&n);
    int pos=0,top=0;
    for(int i=1;i<=n;++i){
    	scanf("%d",&a[i]);
    	pos=top;
    	while(pos&&a[s[pos]]>a[i]) --pos; //若栈顶大于a[i] ，则弹出
    	if(pos) rs[s[pos]]=i;
    	if(pos<top) ls[i]=s[pos+1];
    	s[top=++pos]=i;
    }
    long long l=0,r=0;
    for(int i=1;i<=n;++i){
    	l^=1LL*i*(ls[i]+1);
    	r^=1LL*i*(rs[i]+1);
    }
    printf("%lld %lld",l,r);
    return 0;
}