动量定理与密歇尔斯基方程

上次是英语那这次就是C++

动量(线动量)

定义：

$$\begin{cases} \vec{F}dt = d\vec{P}\\ \int_{t_1}^{t_2}\vec{F}dt = \vec{P_t} - \vec{P_0} \end{cases}\\ \vec{I} = \Delta\vec{P} = \int_{t_1}^{t_2}\vec{F}dt$$

以火箭飞行原理为简单模型举例，分析一个通过将自身一部分物体向反方向给予一初速度（即喷气）的火箭的运动状态。假设 $t$ 时刻箭体的质量为 $m$ ，取成研究的质点系。
分别求得 $t$ 时刻和 $t + dt$ 时刻的动量为

$$\begin{cases} \vec{P_1} = m\vec{v}\\ \vec{P_2} = (m + dm)(\vec{v} + d\vec{v}) + (-dm)\vec{v}^{'} \end{cases}$$

由动量定理，得

$$\vec{F}dt = \vec{P_2} - \vec{P_1}\\ \vec{F}dt = (m + dm)(\vec{v} + d\vec{v}) + (-dm)\vec{v}^{'} - m\vec{v}\\ \vec{F} = \frac{d(m\vec{v})}{dt} - \vec{v}^{'}\frac{dm}{dt}$$

(其中 $dmd\vec{v}$ 为二阶无穷小被略去)
这里我们引入一个向量 $\vec{u}=\vec{v}^{'} - \vec{v}$ ，其物理意义是气体相对于箭体的速度，则可将方程进一步化简为

$$\vec{F} = \frac{\vec{v}dm + md\vec{v}}{dt} - \vec{v}^{'}\frac{dm}{dt}\\ \vec{F} = m\frac{d\vec{v}}{dt} - \vec{u}\frac{dm}{dt}$$

此即为密歇尔斯基方程。
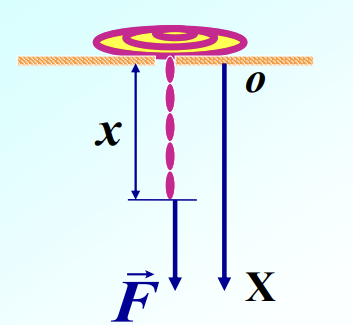
下面进入写这篇笔记最想讨论的一个例题，链条盘于桌子边缘下落的问题。
偷个懒，图片直接截PPT了，侵删。

如图，一长为 $L$ 质量为 $M$ 的链条盘绕在桌子边缘，其中一端在 $t=0$ 时刻开始从桌子边缘初速度为 $0$ 落下，求链条刚好完全从桌子落下时的速度。
这一模型在学习牛顿定律的时候被第一次提及。当时使用的是直接对链条进行受力分析得到

$$\begin{cases} \vec{F} = m_x\vec{g} = \frac{M}{L}x\vec{g}\\ F = \frac{d(m_xv)}{dt} \end{cases}\\ \therefore \frac{M}{L}xg = \frac{d(\frac{M}{L}xv)}{dt}\\ xgdt = d(xv)\\ 左右同乘xv得\\ x^2vg\cdot dt = \frac{1}{2}d(x^2v^2)\\ \because v = \frac{dx}{dt}\\ \therefore x^2vgdt = x^2\frac{dx}{dt}gdt = x^2gdx\\ \therefore \int_{0}^{L^2v_末^2}\frac{1}{2}d(x^2v^2) = \int_{0}^{L}x^2gdx\\ \frac{1}{2}L^2v_末^2 = \frac{1}{3}gL^3\\ v_末 = \sqrt{\frac{2}{3}gL}$$

这一计算方式直观但较为复杂，如果应用密歇尔斯基方程求解，则可以简化一些。
顺带一提，这里的结论倒推回去会发现并不符合能量守恒，这是因为在该理想模型下，即将下落的链条是瞬间获得速度的，其中必会产生大量热，导致能量不守恒。
与之前的火箭模型不同，这里随着链条的下落，原来"箭体"的部分的质量在增加而非减少。但是，密歇尔斯基方程并不一定要求是一种"整体抛弃部分质量"的情景，如果把质量增加理解成"质量减少负值"，或需要清晰一些。公式中的 $\vec{u}$ 在这里表示静止的链条相对下落链条的速度，即 $\vec{u} = -\vec{v}$ ，故有

$$F = m\frac{dv}{dt} + v\frac{dm}{dt} = \frac{d(mv)}{dt} = \frac{d(\frac{M}{L}xv)}{dt}$$

剩下的部分就和第一种解法一致了。
好吧好像也没简化到哪去
但这个例子可以反映出用动量相关定理解题的一个优点：动量守恒等定理是基于牛顿定律，不会出现由于未被考虑的能量消耗而失效。
还有一个提起柔软长绳的问题，与这个题有些区别，但是我感觉能直接牛顿定律受力分析秒了，不太有典型性。

角动量

定义

$$\begin{cases} \vec{L} = \vec{r}\times\vec{P}\;角动量\\ \vec{P} = m\vec{v}\;\;\;\;\;线动量\\ \vec{M} = \vec{r}\times\vec{F}\;力矩 \end{cases}$$

( $\vec{r}$ 需要指出参考点)
简单推导可得

$$\frac{d\vec{L}}{dt} = \frac{d(\vec r \times \vec P)}{dt} = \frac{d\vec r}{dt}\times \vec P + \vec{r} \times \frac{d\vec P}{dt}\\ \because \frac{d\vec r}{dt}\times \vec P = \vec v \times m\vec v = 0\\ \therefore \frac{d\vec L}{dt} = \vec r \times \frac{d\vec P}{dt} = \vec r \times \vec F = \vec M$$

由此得到微分形式和积分形式的角动量定理

$$\begin{cases} \vec Mdt = d\vec L\\ \int_{0}^{t}\vec Mdt = \int_{\vec{L_0}}^{\vec{L_t}}dL = \vec{L_t} - \vec{L_0} \end{cases}$$

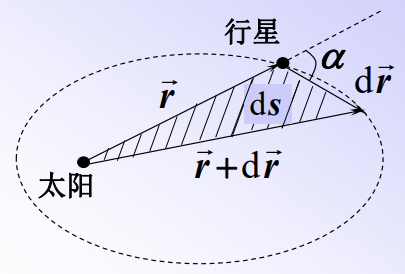
基础应用：证明开普勒第二定律，即行星与太阳的连线在相同时间内扫过相等的面积。
证：行星所受的万有引力的方向恒过太阳的质心，所以以太阳的质心为参考点时，$\vec r$ 与 $\vec F$ 始终平行，因而有角动量守恒，即 $\vec r \times \vec v$ 守恒。
对行星的运动进行微分，得到下图（图自PPT，侵删）

由正弦定理有

$$ds = \frac{1}{2}r|d\vec r|sin\alpha = \frac{1}{2}|\vec r \times d\vec r|\\ 又\because d\vec r = \vec vdt\\ \therefore \frac{ds}{dt} = \frac{1}{2}\mid\vec r \times \frac{d\vec r}{dt}\mid \\ = \frac{1}{2}|\vec r \times \vec v|$$

因此面积速度 $\frac{ds}{dt}$ 为一常量，开普勒第二定律得证。
引：在光滑的水平桌面上有一小孔, 一细绳穿过小孔, 其一端
系一小球放在桌面上, 另一端用手拉绳, 开始时小球绕孔运动,
速率为 $v_1$ , 半径为 $r_1$ , 当半径变为 $r_2$ 时, 求小球的速率 $v_2$ 。
取小孔所在位置 $O$ 为参考点，与开普勒第二定律证明一样，显然有小球角动量守恒。又因为速度的方向始终与受力半径垂直，于是有

$$\vec{L_2} = \vec{L_1} \\ L_2 = L_1\\ r_1mv_1 = r_2mv_2\\ v_2 = \frac{r_1v_1}{r_2}$$

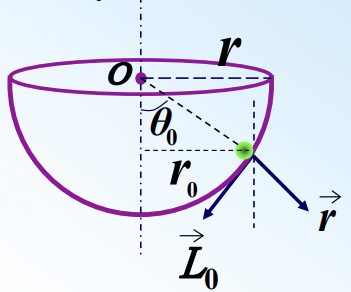
现在来考虑另一个情景：如图，将一个质点沿一个半径为 $r$ 的光滑半球形碗的内表面
水平地投射,碗保持静止。设 $v_0$ 是质点恰好能达到碗口所需要的初速度。试求出 $v_0$ 作为 $\Theta_0$ 的函数的表达式。（图自PPT，侵删）

小球此时受到碗壁所给的指向 $O$ 的弹力和重力。若将 $O$ 设置为参考点，则碗的弹力作用力矩为0，而重力的作用力矩非0，角动量并不守恒。但是，由于合力的力矩 $\vec M = \vec r \times \vec F$ 方向垂直向里，即垂直于 $y$ 轴，所以力矩沿 $y$ 轴方向的分量 $M_y = 0$ ，故在 $y$ 方向上的角动量分量 $L_y$ 守恒。
于是一通推导可得

$$L_0 = rmv_0\sin90^\circ = rmv_0\\ L_{0y} = L_0\sin \Theta_0 = rmv_0\sin \Theta_0 = mv_0r_0\\ L_y = L = rmv\sin90^cir = mvr\\ \because L_{0y} = L_y (角动量分量守恒)\\ \therefore mv_0r_0 = mvr$$

结合机械能守恒可得

$$\begin{cases} mv_0r_0 = mvr\\ \frac{1}{2}mv_0^2 = \frac{1}{2}mv^2 + mgr\cos\Theta_0\\ r_0 = r\sin\Theta_0\\ \end{cases}\\ 解得 v_0 = \sqrt{\frac{2gr}{\cos\Theta_0}}$$

这何尝不是一种引里面的小球模型呢。
或许以后动量能量方程联立还会有非常多，我猜。
断网了，赶紧收工。