有关科里奥利力

upd 4.28
半期考试的题答案与我想的有出入。重新查了一下书，可能我先前的结论有很大的问题。稍后修锅。更改处会注明。
另：半期过后课就少多了，饼先画在这里，把没写完的全部补上。尽量。

源自在物理课上想着出勤而没当场搞懂遂在第二周的早八英语课上重新研究的结论。
先把科里奥利力的公式放在这里：

\[\overrightarrow{F_科} = 2 m \overrightarrow{v} \times \overrightarrow{\omega} \]

我们暂时抛开向量相关不谈，因为在最简单的假设中，\(\overrightarrow{\omega}\) 与 \(\overrightarrow{v}\) 始终垂直，故如果只按照标量进行计算则可得:

\[F_科 = 2m\,v\,\omega \]

升级到向量层面的考虑就留到以后来探索吧

---

修正
此处的公式应该分别改为

\[\overrightarrow{F_科} = 2 m \overrightarrow{v'} \times \overrightarrow{\omega}\\ F_科 = 2m\,v'\,\omega \]

这里的 \(v'\) 表示旋转参考系下物体运动速度
另外也不用以后来探索了，这里向量的情况直接正交分解分别计算出各方向的科里奥利力在算回来就可以了。

---

下面构建一个比较简单的科里奥利力存在的模型(与课上讲的相同):


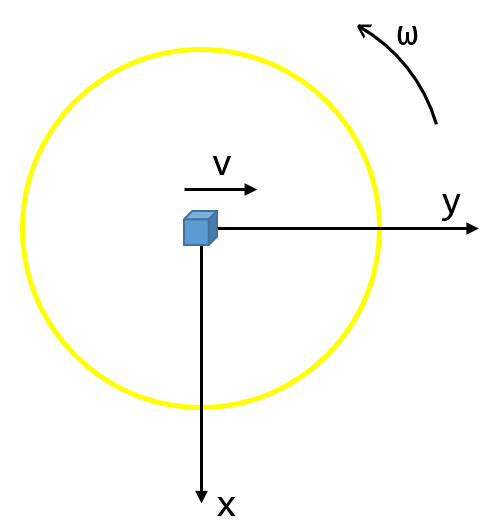
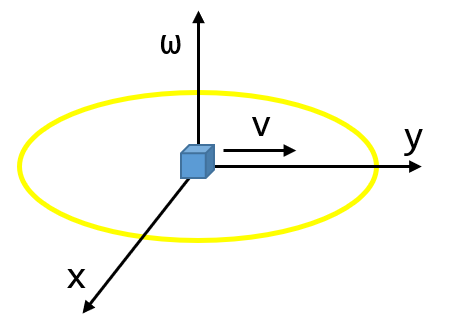
如图，一个光滑圆盘以 \(\omega\) 的角速度匀速逆时针转动，现将一质量为 \(m\) 的小物块放置在圆心并使其以 \(v\) 的速度向右匀速运动，求以圆盘为参照物的参考系中小物块的受力分析。

首先是按照课堂PPT给出的解法：
显然小物块的位移与时间的关系式非常容易得到，即

\[\begin{cases} x' = v\,t\,sin(\omega\,t)\\ y' = v\,t\,cos(\omega\,t) \end{cases} \]

那么根据 \(a = \frac{d^2x}{dt^2}\) 易得小物块正交分解后的加速度，即

\[\begin{cases} a_x = v\,\omega[2cos(\omega\,t)\,-\,\omega\,t\,sin(\omega\,t)]\\ a_y = -\,v\,\omega[2sin(\omega\,t)\,+\,\omega\,t\,cos(\omega\,t)] \end{cases} \]

于是可以求得合力，即

\[F_合 = m\,a_和 = m\, \sqrt{ {a_x}^2 + {a_y}^2 } = m\,v\,\omega\,\sqrt{ {\omega}^2 \, t^2 + 4 } \]

而惯性离心力可以通过切向速度以及当前位移表示出来，即

\[F_离 = m\,r\,\omega^2 = m\,v\,t\,\omega^2 \]

勾股定理可求得垂直于 \(\overrightarrow{v}\) 和 \(\overrightarrow{\omega}\) 的科里奥利力为

\[F_科 = \sqrt{ {F_合}^2 - {F_离}^2 } = 2\,m\,v\,\omega \]

那么为什么这个合力可以按照惯性离心力和科里奥利力进行正交分解？我的理解是，不妨将小物块的速度按照法向速度和切向速度进行分解。法向速度是恒定的，即 \(v\) ，因此这里可以视为仅切向速度受到了惯性力的影响。切向速度所导致的运动状态是一种半径在不断变大的匀速圆周运动。由于其每一刻的切向运动状态为匀速圆周运动，故其法向加速度就是惯性离心加速度。从而可以得出，当合力按照法向和切向进行正交分解时，法向方向的受力就是惯性离心力。

---

修正
现在看来这里问题实在是太大了。可能需要重新写一遍。
首先一个问题就是这里的离心力方向反了。当时我就确实没有认真想清楚所谓"惯性离心力"到底是什么意思。惯性力的产生是因为非惯性系自带加速度，而与之对应原本在惯性系中的物体在惯性系中有相对运动产生的加速度，因此它是一个只由物体位置决定的惯性力，即 $ F_离 = mr\omega^2 $ ，方向沿该位置与转轴的连线向外。在这里，$ F_离 = mr\omega^2 = mvt\omega^2 $
所以上述勾股定理是完全错误的，它的成立是一种巧合，即刚好科里奥利力的沿惯性离心力方向分量与惯性离心力的矢量加和与惯性离心力大小相等方向相反，所以才有所谓勾股定理。也是由于此处的问题，科里奥利力的表达式缺少了一个 \(2mr\omega^2\) ，很阴差阳错地，这个差距正好就是 \(\vec{v'}-\vec{v}\) 这一速度分量产生的科里奥利力，也就是说，此前错误地将科里奥利力公式里的 \(v\) 理解为对地速度导致的偏差与这里错误的理解错合了。
我想对参考ppt中的推导提出一些修正意见，在我重新读过一遍其推导过程后我感觉其中的符号使用有误导性。除了最开始的部分以外，后面的 \(v'\) 均应该改为 \(v_0\) ，因为，这是一个物体相对于旋转参考系本身就在不停改变速度的情况，此时 \(v'\) 在不断变化，明显与ppt中想要表达的速度不合。

---

由此我们可以产生另一种求得科里奥利力的思路：直接对小物块切向加速度进行分析。
根据前面的结论，切向加速度影响的是切向速度的大小。非常容易的就可以得出一个表达式，即

\[F_科^{'} = m\,\frac{d\,v_切}{dt} = m\,\frac{dr\,\omega}{dt} = m\,\omega\,v_法 = m\,v\,\omega \]

问题是，这与上文中直接求导运算得出的科里奥利力差了一个2倍关系。
事实上思考这个问题废掉了我一整节英语
问题就在于，被我理所当然忽视掉的法向速度在以地面参考系的环境下是恒定的，但在以圆盘为参照物的非惯性系中，它仅是大小不变，而方向在改变。由于其与法向加速度方向重合，因此它也并未收到法向加速度的影响，阴差阳错地，我们解释了直接求导计算方法的正确性。于此同时，改变法向速度的方向的加速度就是切向加速度，而这就是被忽略掉的那"部分"科里奥利力。
不难看出，法向速度的方向旋转与圆盘旋转速度是一致的，因此，可以将法向速度随时间改变的状态视为一种角速度为 \(\omega\) 匀速圆周运动，由此可得"部分"科里奥利力的表达式，即

\[F_科^{''} = m\,v\,\omega \]

---

修正
如果只考虑法向速度的科里奥利力那么上面的推导没有问题，此处我们补充切向速度的科里奥利力推导。
现在考虑另一个模型来简化运算：不计重力，设在一竖直固定杆上用一长为 \(r\) 的绳子牵着一小球并使之以 \(\vec{\omega_0}\) 的速度水平旋转，分析其在以固定杆轴心为转轴，轴转动速度为 \(\vec{\omega_1}\) 的转动参考系下的科里奥利力。
这个模型将法向速度抛去，故我们可以只讨论其在切向上的速度产生的科里奥利力。
在以地面为参考系的情况下，小球的运动状态为角速度为 \(\vec{\omega_0}\) 的匀速圆周运动，受力仅有绳提供的拉力。所以有

\[F_0 = mr\omega_0^2 \]

在旋转参考系下，小球的运动状态为角速度为 \(\vec{\omega_0}-\vec{\omega_1}\) 的匀速圆周运动，所以合力可以表示为

\[F_1 = mr(\omega_0 - \omega_1)^2 \]

而由前面修正的部分所强调的，惯性离心力是只由位置决定的，可以得出

\[F_离 = mr\omega_1^2 \]

根据其在法向上的方向关系，我们可以得出

\[\begin{aligned} F_科 &= F_1 - F_0 + F_离\\ &= -2mr\omega_0 \omega_1 + 2mr\omega_1^2\\ &= 2mr(\omega_1 - \omega_0)\omega_1\\ \because v=&r(\omega_0 - \omega_1)\\ \therefore F_科 &= -2mv\omega_1 \end{aligned} \]

负号不要紧，这里的方向是沿法线方向向内，而此处的 \(v\) 和 \(\omega\) 全部是相同的，根据右手定则，叉乘结果方向是法向向外。所以需要一个符号来对应相反方向。

---

因此，最后真正的科里奥利力的表达式为

\[F_科 = F_科^{'} + F_科^{''} = 2\,m\,v\,\omega \]

---

修正
把刚刚修正的部分补充的切向速度带来的科里奥利力补上，矢量加和就可以得到

\[\begin{aligned} F_科 &= F_法 + F_切\\ &= 2m\vec{v_法}\omega +2m\vec{v_切}\omega\\ &= 2m\vec {v'} \times \vec\omega \end{aligned} \]

另外就是，下面那句太对了，八辈子也搞不清楚。

---

还有很多不严谨之处，下辈子再来弄清楚。