11.10多校联训

T1 a

Sol
典中典考后简单题。考场咋就做不对。
不过反悔贪心确实写的比较少。把所有区间按照左端点排序，然后枚举每个点查看之前尚未匹配的区间是否有与该区间不交的，不交则配对，否则查看是否有已配对的且右端点更加靠左的，有就反悔修改，否则新增一个未配对点。当前未配对和已配对点维护右端点从小到大的堆即可。
Code

#include<bits/stdc++.h>
using namespace std;
namespace io
{
    inline int read()
    {
        int x=0,f=1;char c=getchar();
        while(c<'0'||c>'9'){if(c=='-')f=0;c=getchar();}
        while(c>='0'&&c<='9')x=(x<<1)+(x<<3)+(c&15),c=getchar();
        return f?x:-x;
    }
    inline void print(int x)
    {
        static int s[40],slen;slen=0;
        if(x==0){putchar('0');return;}
        if(x<0)x=-x,putchar('-');
        while(x){s[++slen]=x%10;x/=10;}
        for(int i=slen;i;i--)putchar('0'+s[i]);
        return;
    }
}
using namespace io;
const int maxn=400010;
struct node
{
    int l,r,id;
    bool operator<(const node &x)const
    {
        return l<x.l;
    }
}a[maxn];
int n;
priority_queue<int,vector<int>,greater<int> >qu1,qu2;
int main()
{
    freopen("a.in","r",stdin);
    freopen("a.out","w",stdout);
    n=read();
    for(int i=1;i<=n;i++)
    {
        a[i].l=read();a[i].r=read();
    }
    sort(a+1,a+n+1);
    int ans=0,now;
    for(int i=1;i<=n;i++)
    {
        if(!qu1.empty()&&qu1.top()<a[i].l)
        {
            ans++;qu2.push(a[i].r);qu1.pop();
        }else if(!qu2.empty()&&qu2.top()<a[i].r)
        {
            qu1.push(qu2.top());qu2.pop();
            qu2.push(a[i].r);
        }else qu1.push(a[i].r);
    }
    print(ans);putchar('\n');
    return 0;
}

T2 b

显然我不会

T3 c

Sol
考试的时候试着下了两把，很快就搞清楚是个啥意思了。
先手先开一个连通块，为了损失最小显然从小的开始。后手显然要把先手开的这个连通块处理掉，否则净亏。
把所有连通块分为环和链。搜索记录其长度。显然1-链是强制交换先后顺序，对于2-链，情况如下：

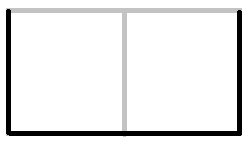
显然先手不会这样填

因为这样相当于把选择权交给后手，所以先手必然选择这样填

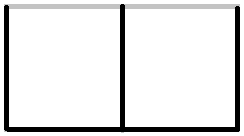
因此2-链与1-链是一样的意义。
对于n-链(\(n\geq 3\))：

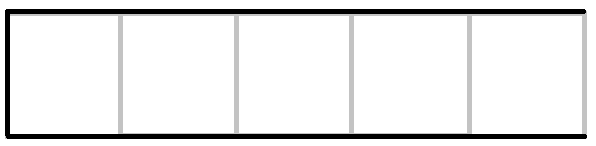
后手都有两种选择：全部吃完，然后交换先后手权

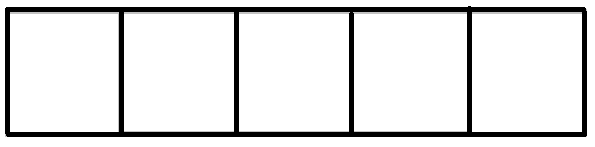
留两个，保留先后手权

对于环上的情况类似，只不过后手要保留先后手权的代价是4个

那么就显然可以搜索当前后手如何选择最优。
然后显然这个搜索可以改成DP，就做完了。
首先处理1-链和2-链，剩下的设\(dp_{i,j}\)表示还剩i个链j个环，那么对于上一个填完的是链的情况，有
\(dp_{i,j}=\max (dp_{i,j},\min (dp_{i+1,j}+4,-dp_{i+1,j})-sizel_i)\)
对于上一个填完的是环的情况，有
\(dp_{i,j}=\max (dp_{i,j},\min (dp_{i,j+1}+8,-dp_{i,j+1})-sizec_j)\)
（\(sizel,sizec\)分别表示环和链大小）
表示从上一状态选择保留先后手还是选择交换先后手。
最后的答案就是前面的1-链，2-链的结果+目前先手/后手对应\(dp_{1,1}\)/\(-dp_{1,1}\)。
Code

#include<bits/stdc++.h>
using namespace std;
const int maxn=30,inf=1000000000;
char s[maxn];
int ditu[maxn][maxn],gpc,nows;
int flag;
bool ban[maxn][maxn][4],vis[maxn][maxn];//上下左右 
const int xx[4]={-1,1,0,0},yy[4]={0,0,-1,1};
int cir[400],lin[400],cirlen,linlen;
int n,m;
int dp[maxn<<1][410];
inline void dfs(int x,int y,int cl,int la)
{
    ditu[x][y]=cl;nows++;
    for(int i=0;i<=3;i++)
    {
        if(i==la)continue;
        if(ban[x][y][i])continue;
        int tox=x+xx[i],toy=y+yy[i];
        if(tox==0||toy==0||tox>n||toy>m){flag=1;continue;}
        if(ditu[tox][toy]==cl)
        {
            flag=-1;
            return;
        }
        dfs(tox,toy,cl,i^1);
    }
    return;
}
inline void check()
{
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)printf("%2d ",ditu[i][j]);
        cout<<endl;
    }
    for(int i=1;i<=cirlen;i++)cout<<cir[i]<<' ';cout<<endl;
    for(int i=1;i<=linlen;i++)cout<<lin[i]<<' ';cout<<endl;
}
int main()
{
    freopen("c.in","r",stdin);
    freopen("c.out","w",stdout);
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n+1;i++)
    {
        scanf("%s",s+1);
        for(int j=1;j<=m;j++)
        {
            if(s[j]=='1')
            {
                ban[i-1][j][1]=1;
                ban[i][j][0]=1;
            }
        }
    }
    for(int i=1;i<=n;i++)
    {
        scanf("%s",s+1);
        for(int j=1;j<=m+1;j++)
        {
            if(s[j]=='1')
            {
                ban[i][j-1][3]=1;
                ban[i][j][2]=1;
            }
        }
    }
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            if(!ditu[i][j])
            {
                if(ban[i][j][0]&ban[i][j][1]&ban[i][j][2]&ban[i][j][3])continue;
                gpc++;flag=0;nows=0;dfs(i,j,gpc,4);if(flag==1)lin[++linlen]=nows;if(flag==-1)cir[++cirlen]=nows;
            }
        }
    }
    int nowf=-1,ans=0,zyw;
    sort(lin+1,lin+linlen+1);
    sort(cir+1,cir+cirlen+1);
    for(zyw=1;zyw<=linlen&&lin[zyw]<=2;zyw++)
    {
        ans+=nowf*lin[zyw];nowf=-nowf;
    }
    for(int i=linlen+1;i>=zyw;i--)
    {
        for(int j=cirlen+1;j;j--)
        {
            if(i>linlen&&j>cirlen)continue;
            dp[i][j]=-inf;
            if(i<=linlen)dp[i][j]=max(dp[i][j],min(dp[i+1][j]+4,-dp[i+1][j])-lin[i]);
            if(j<=cirlen)dp[i][j]=max(dp[i][j],min(dp[i][j+1]+8,-dp[i][j+1])-cir[j]);
        }
    }
    nowf=-nowf;
    printf("%d\n",ans+nowf*dp[zyw][1]);
//    check();
    return 0;
}

T4 d

多项式拉格朗日插值，当然不会。
不过听说可以分块打表，但我还是不会，太菜没办法/kk。