10.30多校联训

T1 删数游戏

Sol
直接全部数字加起来减一然后除以9就可以了，非常好证正确性。
Code
懒得粘。

T2 格点迷踪

Sol
构造题。首先考虑直径最小的构造方案：先看\(n,m\)中有至少一个为奇数：取出奇数那一维的中轴线，然后线上每个点向两边一直延伸即可。

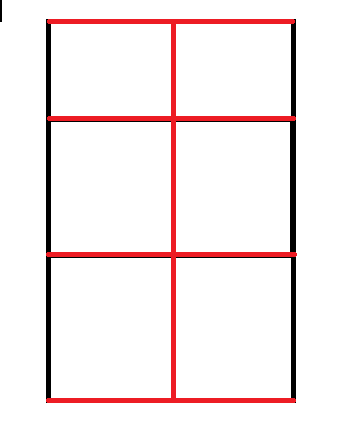
每次延长直径就把边上的延伸线撇过来。

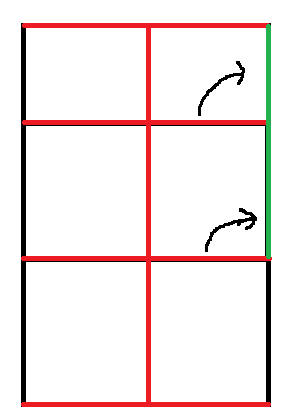
按照这个逻辑不断撇就可以了。
如果\(n,m\)均为偶数，要注意无法实现直径为对角线曼哈顿距离，要特判。
Code
\(Tell\ is\ easy,\ however\ I\ can't\ show\ you\ the\ code.\ Cause\ it's\ too\ hard\ for\ me\ to\ write\ that.\)

T3 沙漠绿洲

Sol
首先可以证明：每一条边最多只走一次。那么其实就是花费\(dis(u,v)\)把\(u,v\)联通起来。
最开始我想的是直接枚举点集，然后跑\(kruskal\)计算答案取最值，然后发现\(n=2\)的小数据全过，大样例死活过不了。
然后就发现可能选出来的点集并不只形成一个最小生成树，而是一个最小生成森林。所以可以套上一个状压DP，把原来计算的答案改成只计算处在树中的数的最小值。
这样每种状态表示对应二进制位上是否被考虑。设\(g(now)\)表示当前状态最优答案，\(f(now)\)表示当前状态全部在同一树上的答案。那么答案有

\[g_{now}=\max_{i\&now=i} min(g_i,g_{now\ xor\ i}) \]

\(g(now)\)初始值是\(f(now)\)
加一个记搜，时间复杂度\(O(2^{2n})\)，这样的话\(n=16\)会被卡，如何优化我也不知道。。。但是对于\(60\)分的优化是很好想的：因为所有点在同一数轴上，所以选择的边肯定是一段连续区间才最优，所以状压DP状态枚举可以改成枚举区间起点终点，变成\(O(2^n*n^2)\)。
Code（不带优化）

#include<bits/stdc++.h>
using namespace std;
const int maxn=20;
int n;
double a[maxn],b[maxn],c[maxn];
double dis[maxn][maxn],rst;
bool con[maxn];
int fa[maxn],len,siz[maxn];
double cost[maxn],wat[maxn];
struct edge
{
    int from,to;
    double v;
    bool operator<(const edge &x)const
    {
        return v<x.v;
    }
}di[maxn*maxn];
inline int findf(int x)
{
    if(fa[x]==x)return x;
    return fa[x]=findf(fa[x]);
}
double f[65546],g[65546];
inline void klske()
{
    for(int i=1;i<=n;i++)fa[i]=i,cost[i]=0,wat[i]=c[i],siz[i]=1;
    int now=1,al=0;
    for(int i=1;i<=n;i++)if(con[i])al++;
    if(al<2)
    {
        double an=1000000000.0;now=0;
        for(int i=1;i<=n;i++)
        {
            if(con[i])
            {
                now|=(1<<i-1);
                an=min(an,c[i]);
            }
        }
        f[now]=an;
        return;
    }
    for(int i=1;i<=len;i++)
    {
        if(con[di[i].from]==0||con[di[i].to]==0)continue;
        int x=di[i].from,y=di[i].to;
        double val=di[i].v;
        x=findf(x),y=findf(y);
        if(x==y)continue;now++;
        fa[x]=y;siz[y]+=siz[x];wat[y]+=wat[x];cost[y]+=cost[x]+val;
        if(now==al)break;
    }
    double an=1000000000.0,an1=1000000000.0;
    now=0;
    for(int i=1;i<=n;i++)
    {
        if(!con[i])continue;
        now|=(1<<i-1);
        if(fa[i]==i)an=min(an,(wat[i]-cost[i])/(siz[i]));
        an1=min(an1,c[i]);
    }
    f[now]=max(an,an1);
    return;
}
inline void dfs(int step)
{
    if(step==n+1)
    {
        klske();
        return;
    }
    con[step]=1;dfs(step+1);
    con[step]=0;dfs(step+1);
    return;
}
inline double getans(int zt)
{
    if(g[zt]>=0)return g[zt];
    g[zt]=f[zt];
    for(int i=1;i<=zt;i++)
    {
        if(i==zt)break;
        if((i&zt)==i)g[zt]=max(g[zt],min(getans(i),getans(i^zt)));
    }
    return g[zt];
}
signed main()
{
    freopen("desert.in","r",stdin);
    freopen("desert.out","w",stdout);
    scanf("%d",&n);
    memset(g,-1,sizeof(g));
    for(int i=1;i<=n;i++)
    {
        scanf("%lf%lf%lf",&a[i],&b[i],&c[i]);
    }
    for(int i=1;i<=n;i++)
    {
        for(int j=i+1;j<=n;j++)
        {
            dis[i][j]=sqrt((a[i]-a[j])*(a[i]-a[j])+(b[i]-b[j])*(b[i]-b[j]));
        }
    }
    for(int i=1;i<=n;i++)
    {
        for(int j=i+1;j<=n;j++)di[++len]=(edge){i,j,dis[i][j]};
    }
    sort(di+1,di+len+1);
    dfs(1);
    getans((1<<n)-1);
    printf("%.10lf\n",g[(1<<n)-1]);
    return 0;
}

T4 奇异函数

不会。