P1852 跳跳棋

Prob

题目大意

依照跳棋的规则，求至少多少步将三颗跳棋的初始状态转移到目标状态
规则：越过相邻的棋子并使该棋子成为移动前后位置的中点，不能越过两颗以上的棋子（即如按规则越过两颗就无法进行此操作）

Solution

如果没有讲这道题我是真想不到用树的思想做。
考虑每次的状态转移：中点跳向两边、两边越过中间。
由于过程可逆，只考虑两边跳向中间。
根据规则，左和右至多只有一边的跳跃是合法的，即离中点远的那个点跳跃会越过两个点。
如此做三个点的间距会越来越短，而末状态是两边的点与中点距离相同。
反过来想：从末状态不断由中间点向两边跳开，就是一棵二叉树。而末状态就是树根。如图是一个以\(4,\;5,\;6\)为初状态的树。

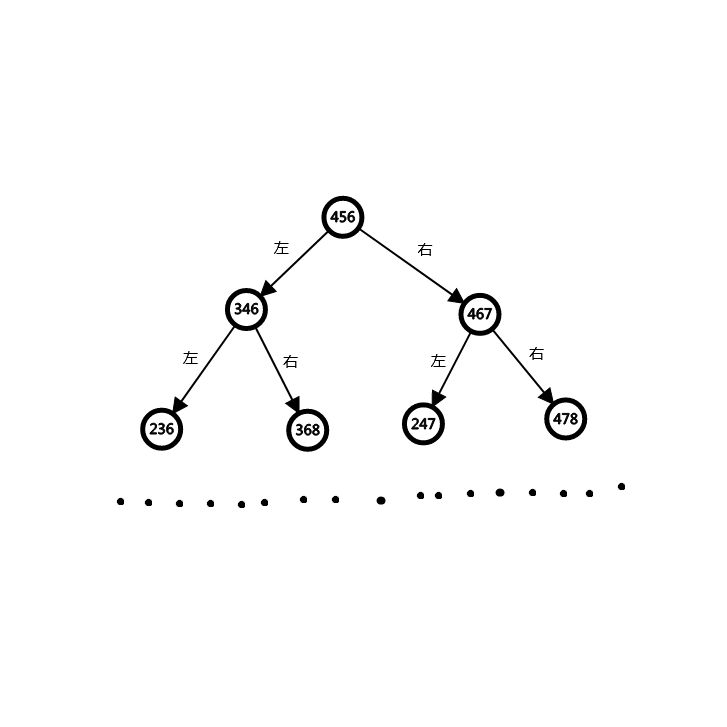
如果初末状态的树根不同，那必然无法转移，输出\(-1\)。
对于在同一棵树上，其实和树上求距离很像。
但是无法使用求\(LCA\)的常规倍增或线段树，因为不知道边界。
考虑一次状态转移。假设当前状态是\(x,\;y,\;z\;(x<y<z)\)，设\(d1=y-x,d2=z-y\)。
假如\(d1>d2\)（反之同理），那么一次转移以后的状态变为\(x,\;z-d2*2,\;y\)，由于\(d2=y-z\)，所以实际状态为\(x,\;y-d2,\;z-d2\)，也就是将右边两个点向左移动\(d2\)的长度。
如果出现例如\(1,\;1000,\;1001\)这种状态，那么其实浪费了大量的时间做重复的转移方式。
设\(d3=(d1-1)/d2\)，那么在求根的过程中会重复执行\(d3\)次当前操作，可直接省略为\(x,\;y-d3*d2,\;z-d3*d2\)，而剩下的距离长度\(d1-=d3*d2\)，相当于\(d1=(d1-1)%d2+1\)。
显然之后的过程就是反过来把左边两点向右移，不难发现这个过程与\(gcd\)中的辗转相除类似，时间复杂度\(O(logn)\)。
借用倍增求\(LCA\)的思路，在找根的过程中每次将\(dep+=d3\)求状态深度，然后先将初末状态中较深的一个先转移\(\Delta dep\)次。
对于转移函数\(jump\)：递归地向上找，如果当前\(d3>=ldep\)，则返回状态\(x,\;y-ldep*d2,\;z-ldep*d3\)；如果\(d3<ldep\)，则先转移状态改成\(x,\;y-d3*d2,\;z-d3*d2\)，再返回\(jump(x,\ y,\ z,\ ldep-d3)\)（\(d1<d2\)同理）。
然后利用二分求上移深度，如果状态相同则\(r=mid\)，不同则\(l=mid+1\)，注意\(mid=(l+r+1)/2\)。
最后求得\(ans=\Delta dep+l*2\)。
输入不保证按照从小到大，坑死

Code

#include<bits/stdc++.h>
#define int long long
using namespace std;
struct node
{
	int x,y,z;
};
inline node getgen(int x,int y,int z,int &dep)
{
	int d1=y-x,d2=z-y;
	if(d1==d2)return (node){x,y,z};
	int d3=(max(d1,d2)-1)/min(d1,d2);dep+=d3;
	if(d1> d2)return getgen(x,y-d3*d2,z-d3*d2,dep);
	if(d1< d2)return getgen(x+d3*d1,y+d3*d1,z,dep);
}
inline void jump(int &x,int &y,int &z,int ldep)
{
	int d1=y-x,d2=z-y;
	if(d1==d2)return;
	int d3=(max(d1,d2)-1)/min(d1,d2);
	if(d3>=ldep)
    {
    	if(d1>d2)y-=ldep*d2,z-=ldep*d2;
    	else x+=ldep*d1,y+=ldep*d1;
    }else
    {
    	if(d1>d2)y-=d3*d2,z-=d3*d2;
    	else x+=d3*d1,y+=d3*d1;
    	jump(x,y,z,ldep-d3);
    }
	return;
}
inline bool check(int lim,int a,int b,int c,int x,int y,int z)
{
	jump(a,b,c,lim);jump(x,y,z,lim);
	if(a==x&&b==y&&c==z)return 1;
	return 0;
}
signed main()
{
	int a,b,c,x,y,z,depa=0,depb=0;
	scanf("%lld%lld%lld%lld%lld%lld",&a,&b,&c,&x,&y,&z);
	if(a>b)swap(a,b);if(b>c)swap(b,c);if(a>b)swap(a,b);
	if(x>y)swap(x,y);if(y>z)swap(y,z);if(x>y)swap(x,y);
	node A=getgen(a,b,c,depa),B=getgen(x,y,z,depb);
	if(A.x!=B.x||A.y!=B.y||A.z!=B.z)return printf("NO\n")&0;
	printf("YES\n");
	int ans=abs(depa-depb);
	if(depa<depb)jump(x,y,z,depb-depa);
	else jump(a,b,c,depa-depb);
	depa=depb=min(depa,depb);
	if(a==x&&b==y&&c==z)return printf("%lld\n",ans)&0;
	int l=1,r=depa;
	while(l<r)
    {
    	int mid=(l+r)>>1;
    	if(check(mid,a,b,c,x,y,z))r=mid;
    	else l=mid+1;
    }
	printf("%lld\n",ans+l*2);
	return 0;
}