OO_第一单元总结

OO_第一单元总结

第一次作业

一、题目要求

 将包含加、减、乘、乘方以及括号（其中括号的深度至多为 1 层）的单变量表达式，输出恒等变形展开所有括号后的表达式。

二、架构

我的建模结构如下

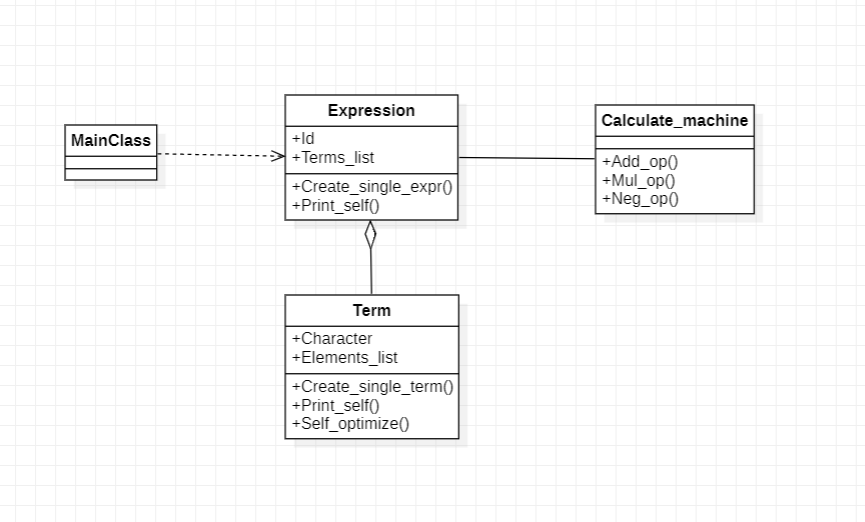
我是用的是预解析模式，对每条运算进行处理。Expression类是运算，存储的基本单元。在存储时，“+”，“-”号将一个表达式分为不同的Term，用一个ArrayList将所有项存起来。每个Term类中，记录该项的符号，并用“*”将数字和x分隔开，用ArrayList将这些存起来。

三、运算

加法

 将参与加法的数字或x转化为表达式。两表达式相加只需将Expression里的Term列表合并即可

减法

 另减数表达式的所有项符号反转，再将两表达式相加即可。

乘法

 将表达式1的每一项与表达式2的每一项两两相乘，项相乘使只需将项的因子列表合并。

四、化简

Term化简

 将所有数字相乘，所有相同的变量记为乘方形式，如 x*x*x 记为 x**3。

Expression化简

 将包含的所有Term化简后合并同类项

五、类复杂度

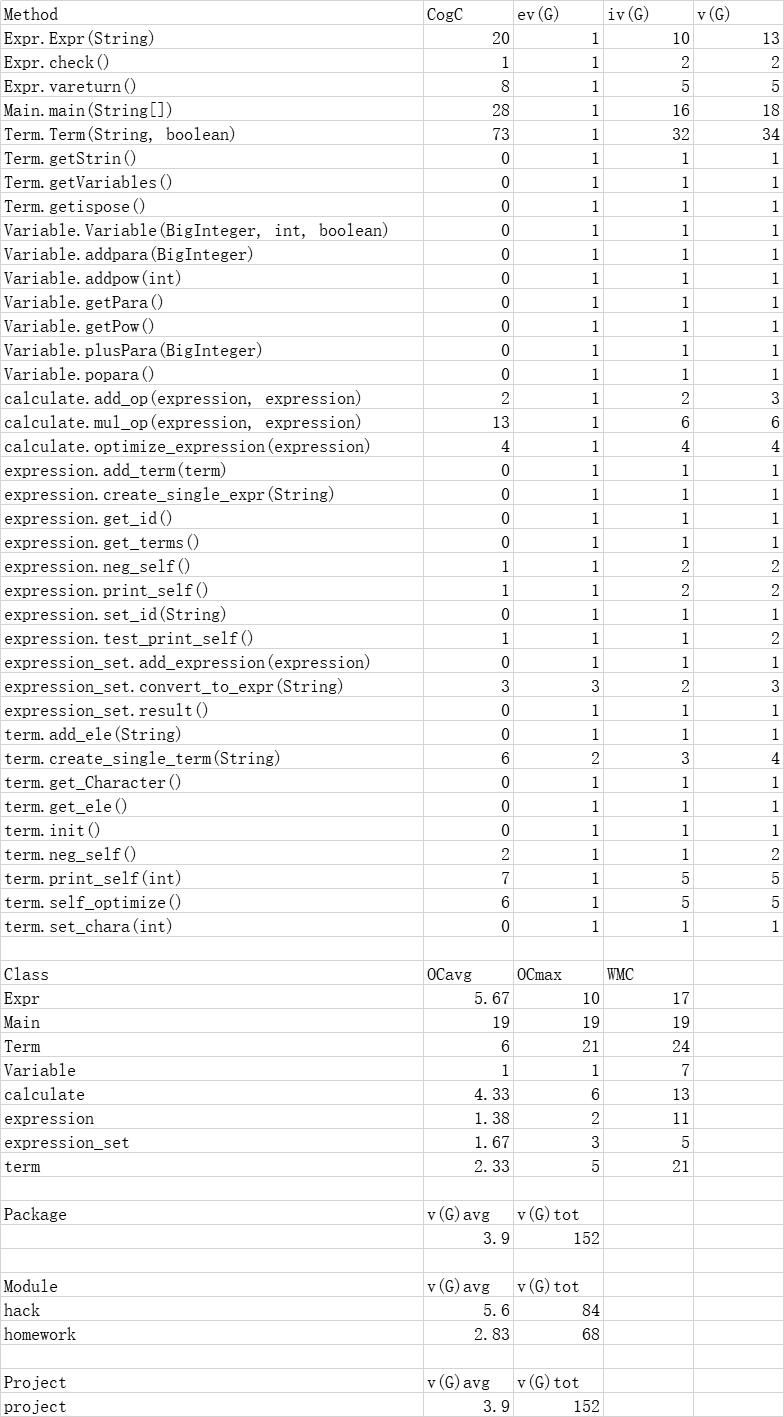
第二次作业

一、题目要求

 读入一系列自定义函数的定义以及一个包含简单幂函数、简单三角函数、简单自定义函数调用以及求和函数的表达式，输出恒等变形展开所有括号后的表达式。

二、迭代策略

 与第一次作业不同的是加入了sin和cos运算。运算存储的框架可保持第一次作业的版本，在此基础上迭代，我的处理思路是先将sin(cos)的式子映射成新变量。由于括号里的表达式只能是数字或x的乘方。只需对这两种情况分别判断后映射。

三、化简

 合并同类项时，每项的变量由x和sin，cos映射后的变量组成，统计他们出现的次数进行同类型合并。

四、圈复杂度

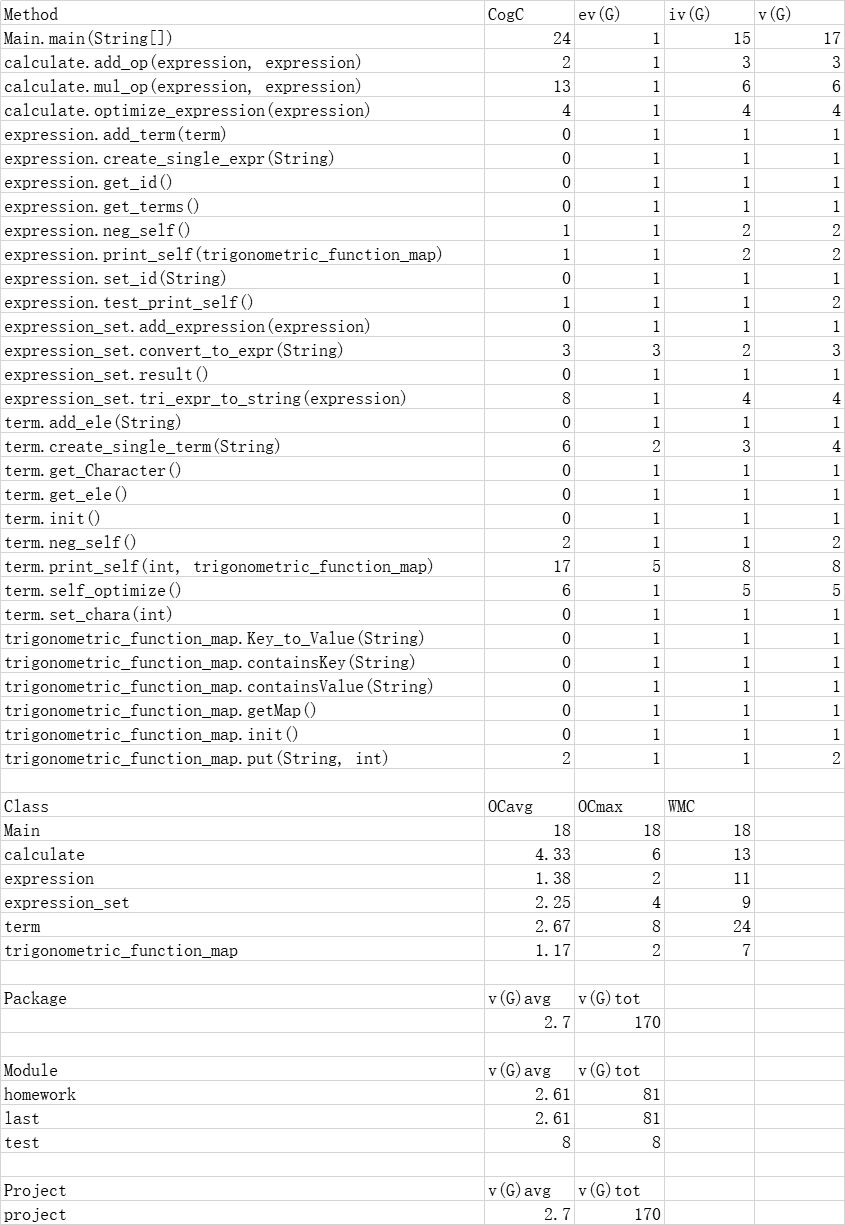
第三次作业

一、题目要求

 读入一系列自定义函数的定义以及一个包含幂函数、三角函数、自定义函数调用以及求和函数的表达式，输出恒等变形展开所有括号后的表达式。

二、迭代策略

 本次作业与第二次不同的是sin和cos括号里的表达式可以是多项式，并可以三角函数嵌套。运算存储的框架可保持第二次作业的版本，在此基础上迭代，我的处理思路是先将sin括号里的表达式按照变量的降幂排列，优先级为x，而后是sin,cos表达式组成的新变量建立的次序。将表达式转化为String，再将整个String用HashMap映射成新变量，用新变量来代替整个sin（cos）的式子。由于表达式被降幂排列所以同一个sin式子能被映射成相同的变量。

三、圈复杂度

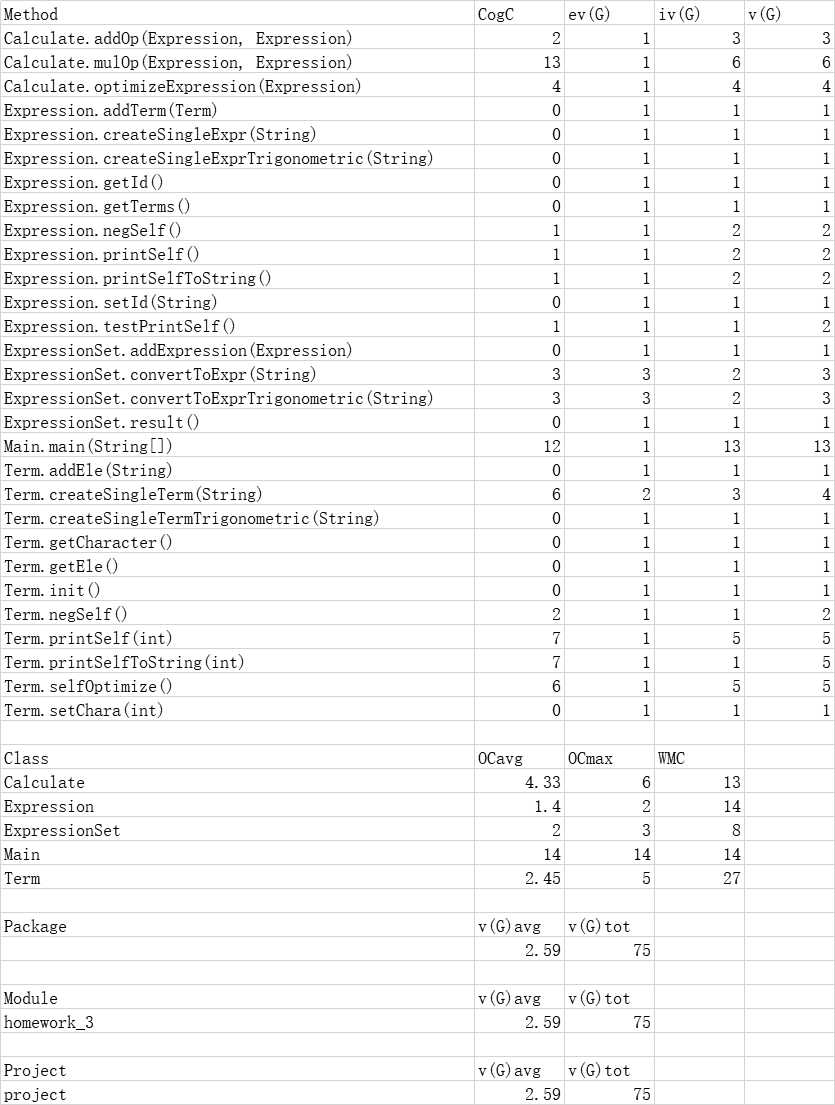
bug修复与分析

 在特判pow的指数时我一开始用了 splitItem[3].equals("0")，带没考虑到 +0 的情况，改后用 Integer.parseInt(splitItem[3]) == 0) 就可以了
 在处理sin（cos）括号里的表达式时没有把新定义的变量翻译成sin（cos）表达式，直接带入的自定义变量导致了错误。改后，在映射前将所有自定义的变量映射回去就修复了。

架构设计

优点：
 代码逻辑清晰。可维护性强。
缺点:
 不能独立处理表达式。耦合度较高。

心得体会

 寒假摸鱼没写pre，导致开学前两周在补寒假的内容，就做了预解析模式。到第三周想做正常模式发现没经验实现不了了。
 对设计模式有了一定了解