codeforces 1194F Crossword Expert

题目链接：https://codeforc.es/contest/1194/problem/F  (中国镜像网站)

题目链接：https://codeforces.com/contest/1194/problem/F

 

题目大意：每个任务会耗时t或者t+1秒。求规定时间会完成任务个数的期望。

PS：碰到好题了，分享一下。

 

思路：可以看出第i任务对答案的期望为(杨辉三角的第i层的前(t-Sum)项的和)/(2的i次方)。Sum是前i个任务规定时间的总和。

0、Sum会越来越大（废话）

1、(t-Sum)<0，该任务对答案没有奉献。(比如样列1的第三个任务。不管怎么样都不会完成这个任务的。）

2、(t-Sum)>=i，该任务一定会发生。比如样列1的第一个任务。

3、(t-Sum)，会越来越小

4、跟据以上三条。发现我们要求的层数是一段连续的层数，并且要求的前(t-Sum)项会越来越少。直到(t-Sum)<0；

证明：概率论的二项式定理看懂了就会了，(杨辉三角的第n层的前k项和)/(2的i次方)等价于抛硬币n次的正面次数不多于k的概率。

 

通过预处理，可以得到n的阶层，n的阶层的逆元。就可以O(1)的求组合函数C(a,b)的值。

所以这个题可以O(n^2)解决了。(通过枚举需要求的第i层的前(t-Sum)项)

PS：比赛是这样写然后超时了。555~~

然后赛后补题发现，组合函数有这个公式。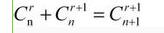

然后，发现，(第n层的前k项和)*2-C(k,n)==(第n+1层的前k项和)。

证明：

 

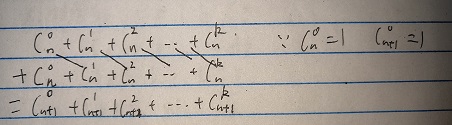
然后就好办了。

1、暴力枚举我们的第一次要求的层数的前(t-Sum)项。

2、根据上述结论算出下一层的前(t-Sum0)项。( (t-Sum0)是上一层的(t-Sum)。加个0以示区别 ）

3、然后减去不这一层不要的后面几项。

4、重复2，3直到结束或者(t-Sum)<0。

 

结束。贴代码。嘻嘻嘻。

#include <bits/stdc++.h>
using namespace std;
#define N 100010
#define int long long
#define mod 1000000007
#define mp make_pair
#define endl '\n'
#define IOS cin.sync_with_stdio(false);cin.tie(0);cout.tie(0);
int A[200010],A_inv[200010];
void init1(){
    int p=mod;
    A_inv[1]=1;
    for(int i=2;i<=200005;++i){
        A_inv[i] = ((p-(p / i)) * A_inv[p % i]%p+p)%p;
    }
    for(int i=2;i<=200005;++i){
        A_inv[i]*= (A_inv[i-1]);
        A_inv[i]%=mod;
    }
    A[0]=1;
    for(int i=1;i<=200005;++i){
        A[i]=A[i-1]*i%mod;
    }
}
int Sum_c;
int Sum_i0;
int C(int n,int i0){
    if(Sum_c==0){
        Sum_c=1;
        for(int i=1;i<=i0;i++){
            Sum_c+=A[n]*A_inv[n-i]%mod*A_inv[i]%mod;
            Sum_c%=mod;
        }
        Sum_i0=i0;
    }
    else{
        int n0=n-1;
        Sum_c=Sum_c*2-A[n0]*A_inv[n0-Sum_i0]%mod*A_inv[Sum_i0]%mod+mod;
        Sum_c%=mod;
        for(;Sum_i0>i0;Sum_i0--){
            Sum_c=Sum_c-A[n]*A_inv[n-Sum_i0]%mod*A_inv[Sum_i0]%mod+mod;
            Sum_c%=mod;
        }
    }
    return Sum_c;
}
int power(int a,int b){
    int ret=1;
    for(int k=a;b;b>>=1,k=k*k%mod){
        if(b&1){
            ret=ret*k%mod;
        }
    }
    return ret;
}
 
signed main(){
init1();IOS;
    int n,t,a;
    cin>>n>>t;
    int Ans=0;
    int rk=1;
    int Sum=0;
    for(int i=1;i<=n;i++){
        rk<<=1;
        rk%=mod;
        cin>>a;
        Sum+=a;
        if(Sum+i<=t){
            Ans++;
            Ans%=mod;
        }
        else if(Sum>t){
            break;
        }
        else{
            Ans+=C(i,t-Sum)*power(rk,mod-2);
            Ans%=mod;
        }
    }
    cout<<Ans;
    return 0;
}
/*
 
*/