Task.1 倾斜的线
题目大意:在平面上有 \(n\) 个点,给定 \(P,Q\),在平面上找到两个点使它们所在直线的斜率数值上最接近 \(\frac{P}{Q}\) 。对于接近程度相同的直线选择较小的斜率。
数据范围:\(2\leq N\leq 2\times 10^5,1\leq P,Q,x,y\leq 10^9\),不存在经过两点的直线斜率为 \(0\) 或正无穷。
在考场想到了一个没那么naive的想法,把坐标系旋转到 \(y\) 轴平行于斜率为 \(\frac{P}{Q}\) 的直线的位置,大概是这样:

算出来每个点在新坐标系中的横坐标是 \(\frac{Px-Qy}{\sqrt{P^2+Q^2}}\),下面非常的恼人,但是和 \(x,y\) 无关,所以让它消失,变成 \(Px-Qy\)。
发现经过横坐标相近的点的直线斜率很接近 \(\frac{P}{Q}\),所以我们按照横坐标排序后去算相邻点在原图中的斜率。
但是这个方法挂了,应该是我写得有问题,其实这个方法已经非常接近正解了,思路上没有什么问题。
我们再把做法变得具体一点:在新坐标系中放许多 \(x=c\) 平行 \(y\) 轴的直线,探讨最优解会在什么地方。
如图:
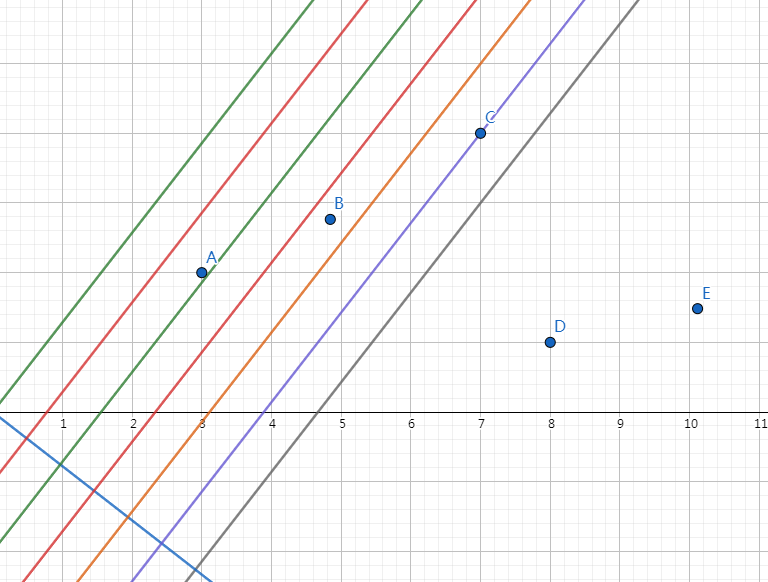
很明显的,对于按 \(x\) 排序后相近的三个点 \(A,B,C\),最优解一定是在 \(AB\) 或 \(BC\) 中取,而不是 \(AC\)(\(B\) 点不管放在过 \(AC\) 直线间的什么位置 \(AC\) 都没有 \(AB,BC\) 优)。
而 \(std\) 给出的做法是每个点以过它本身的斜率为 \(\frac{P}{Q}\) 的直线的截距排序,然后从排序后相邻的点对中计算最优解,正确性的证明与上述过程基本一致。复杂度 \(O(N log N)\)。
实现上的坑点:\(std\) 建议我们写分数类来避免精度误差,但是几乎所有人都是 \(long\ double\) 过去的...
代码:
#include<stdio.h>
#include<string.h>
#include<algorithm>
using namespace std;
template<class T>void read(T &x){
x=0; char c=getchar();
while(c<'0'||'9'<c)c=getchar();
while('0'<=c&&c<='9'){x=(x<<1)+(x<<3)+(c^48); c=getchar();}
}
typedef long long ll;
typedef long double db;
const int N=200050;
const db e=1e-15;
int n;
ll P,Q,p,q;
struct point{ll x,y,c;}a[N];
ll gcd(ll _a,ll _b){return _b==0?_a:gcd(_b,_a%_b);}
ll absl(ll _a){return _a>0?_a:-_a;}
db absd(db _a){return _a>0?_a:-_a;}
bool cmp(point x,point y){return x.c<y.c;}
int main(){
freopen("slope.in","r",stdin);
freopen("slope.out","w",stdout);
read(n); read(P); read(Q);
ll d=gcd(P,Q); P/=d; Q/=d;
for(int i=1,x,y;i<=n;i++){
read(x); read(y);
a[i]=(point){x,y,1ll*Q*y-1ll*P*x};
}
sort(a+1,a+n+1,cmp);
ll tp,tq,p,q;
db r=1e10,t,s=(db)P/(db)Q;
for(int i=1;i<n;i++){
tp=a[i].y-a[i+1].y;
tq=a[i].x-a[i+1].x;
if(tp*tq<0) continue;
tp=absl(tp); tq=absl(tq);
d=gcd(tp,tq); tp/=d; tq/=d;
t=absd((db)tp/(db)tq-s);
if(r-t>e) r=t, p=tp, q=tq;
}
printf("%lld/%lld\n",p,q);
return 0;
}
Task.2 最小值
题目大意:有一个长度为 \(n\) 的序列 \(a\),定义一段区间 \([l,r]\) 的价值为 \(f(min^r_{i=l}a_i)=Ax^3+Bx^2+Cx+D\)。现在需要你把区间分成若干段,求分割后所有区间的价值的最大和。
数据范围:\(1\leq N\leq 2\times 10^5,\forall |f(x)|\leq 10^{13}\),输入的数据均在 \(int\) 范围内。
咋一看式子和求的东西以为是斜率优化?毕竟那个 \(O(N^2)\) 的\(dp\)还是很明显的:\(dp_i=max\{dp_j+f(min^r_{i=l}a_i)\}\)。接下来就是考虑优化它了,变成带 \(log\) 或者线性都会很好。
但是最小值有些棘手,我甚至不知道该怎么描述。但是在转移的过程中,随着 \(i\) 的增加, \(i\) 之前某些区间 \([l,r]\) 内的位置到 \(i\) 的最小值都是相同的,这个时候区间内的最优解一定是 \(dp\) 值最大的那一个。利用这个性质,如果我们能知道哪些区间里的位置到 \(i\) 的最小值相同,我们就能避免一些无用的转移。
这个问题就转化成了求 \(i\) 之前离 \(i\) 最近的位置 \(x\) ,使 \(x\) 之后的位置到 \(i\) 的最小值都是 \(a_x\),再求 \(x\) 之前离 \(x\) 最近的位置 \(y\),使 \(y\) 到 \(x-1\) 的位置到 \(i\) 的最小值都为 \(a_y\) ...... 这个问题就一个经典的单调栈问题,维护一个栈顶到栈底递减的单调栈就可以了。
再利用单调栈来优化转移:当 \(a_i\) 入栈前退栈时,把退栈的位置的最值记录下来,利用退栈的最值更新 \(dp_i\),再把最值也存下来(可以存在栈里)。复杂度 \(O(N)\)。
代码:
#include<stdio.h>
#include<string.h>
#include<algorithm>
using namespace std;
template<class T>void read(T &x){
x=0; bool f=0; char c=getchar();
while(c<'0'||'9'<c){f|=(c=='-'); c=getchar();}
while('0'<=c&&c<='9'){x=(x<<1)+(x<<3)+(c^48); c=getchar();}
x=f?-x:x;
}
typedef long long ll;
const int N=200050;
int n,A,B,C,D;
int a[N],top;
struct node{int i; ll v;}st[N];
ll f[N];
ll F(int x){return 1ll*A*x*x*x+1ll*B*x*x+1ll*C*x+D;}
int main(){
freopen("min.in","r",stdin);
freopen("min.out","w",stdout);
read(n); read(A); read(B); read(C); read(D);
for(int i=1;i<=n;i++) read(a[i]);
ll tmp=0;
for(int i=1;i<=n;i++){
tmp=f[i-1];
while(top&&a[st[top].i]>a[i]) tmp=max(tmp,st[top--].v);
f[i]=tmp+F(a[i]);
if(top) f[i]=max(f[i],f[st[top].i]);
st[++top]=(node){i,tmp};
}
printf("%lld\n",f[n]);
return 0;
}
Task.3 安排
题目大意:给出长度为 \(n\) 的排列 \(A,B\),每次操作可以选择 \(A\) 中的一段区间 \([l,r]\),交换区间内最大值最小值的位置。求一种在 \(345678\) 次内把 \(A\) 变成 \(B\) 的方法。
数据范围:\(1\leq N\leq 4096\)
目前还不会做...
“您能再~讲一遍吗?”

 浙公网安备 33010602011771号
浙公网安备 33010602011771号