Geometry Continuity & Zebra Stripes
Continuity descriptions
A curve or surface can be described as having Gn continuity, n being the increasing measure of smoothness. Consider the segments either side of a point on a curve:
- G0: The curves touch at the join point (position).
- G1: The curves also share a common tangent direction at the join point (tangent).
- G2: The curves also share a common center of curvature at the join point (curvature).
See also: Wikipedia: Geometric continuity
Position (G0)
Position (G0 continuity) measures location only. If the end points of each curve are in the same location in space, the curves are position continuous (G0) at the ends. In other words, the two curves in question touch each other at their end points.
Tangency (G1)
Tangency (G1 continuity) measures position and curve direction at the ends. in other words, the two curves not only touch, but they go the same direction at the point where they touch.
The direction is determined by the first and second point on each curve. If these two points fall on a line, the two curves are tangent at the ends.
The first derivative of the two curves is equal at the point where they touch.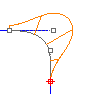
Curvature (G2)
Curvature continuity (G2 continuity) between two curves measures position, direction, and radius of curvature at the ends. If the radius of curvature is the same at the common end point, curves are curvature continuous (G2). In other words, the curves not only go the same direction when they meet, but also have the same radius at that point. This condition is not easy to determine by just looking at where the points are located.
Both the first and second derivatives of the equations are equal at that point.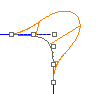
G3
G3 continuity adds a third requirement: planar acceleration. Curves that are G3 continuous touch, go the same direction, have the same radius, and that radius is accelerating at the same rate at a certain point.
G3 continuous curves have equal third derivatives.
G4
G4 continuity is very seldom used, but can be important in certain isolated cases. G4 continuous curves have all the same requirements as G3 curves, but their curvature acceleration is equal in three dimensions.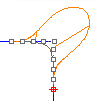
Interpreting the stripes
Position Only (G0)
If the stripes have kinks or jump sideways as they cross the connection from one surface to the next, the surfaces touch, but have a kink or crease at the point where the zebra stripes jag. This indicates G0 (position only) continuity between the surfaces.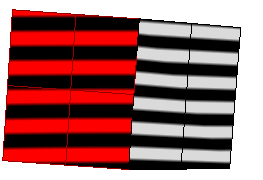
Tangent matches; curvature does not match (G1)
If the stripes line up as they cross the connection but turn sharply at the connection, the position and tangency between the surfaces match. This indicates G1 (position + tangency) continuity between the surfaces. Surfaces that are connected with the FilletSrf command display this behavior.
Position, curvature, and tangency match (G2)
If the stripes match and continue smoothly over the connection, this means that the position, tangency, and curvature between the surfaces match. This matching indicates G2 (position + tangency + curvature) continuity between the surfaces. Surfaces connected with the BlendSrf, MatchSrf, or NetworkSrf commands display this behavior. When you use surface edges as part of the curve network, the NetworkSrf options allow any of these connections.
If, when you use the Zebra command, the selected objects do not already have a surface analysis mesh, an invisible mesh will be created based on the settings in the Polygon Mesh Options dialog box.
The surface analysis meshes save in the Rhino files. These meshes can be large. The RefreshShade command and the Save geometry only option of the Save and SaveAs commands remove any existing surface analysis meshes.
To properly analyze a free-form NURBS surface, the analysis commands generally require a detailed mesh.
https://docs.mcneel.com/rhino/8/help/en-us/popup_moreinformation/continuity_descriptions.htm
https://docs.mcneel.com/rhino/8/help/en-us/commands/zebra.htm
为了方便大家在移动端也能看到我的博文和讨论交流,现已注册微信公众号,欢迎大家扫描下方二维码关注。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号