Logistic 与 softmax
之前写的一篇感觉太 Naive ,这里重新写一篇作为总结。Logistic 与 Softmax 都是一种概率判别模型(PRML p203),Softmax 通常用在 Neural Network 里最后全连接层 ,Logistic 在业界更是普及,因为简单有效、便于并行、计算量小快,适合大规模数据等优点,而且采用 SGD 的 Logistic 相当于直接 Online Learning ,非常方便。本文将对两个模型展开详细介绍,从 exponential family 到 parallel 等都会涉及。
Sigmod Function
Logistic Regression 是用来处理二分类问题的,它与一个函数密切相关,即 sigmod 函数:
\[h(z) = \frac{ e^z}{1+ e^z}= \frac{ 1}{1+ e^{-z}} \]
通过 sigmod 函数可以将函数值映射到 $(0,1)$ 区间,这里 $h$ 即代表了 sigmod 函数,其图形如下: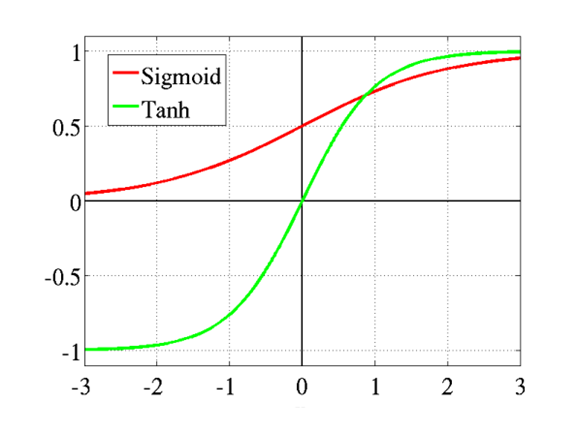
Logistic Regression 正是在线性回归的基础上加了 sigmod 而得到的
对数几率比解释
线性回归中,值域落在 $(-\infty,+\infty)$,然而对于二分类来说只需两种取值 0、1 即可,线性回归中事件发生的几率用 $\frac{p}{1-p}$ 表示的话,其值域为 $[0,\infty)$ ,然而二分类中模型取值落在 $[0,1]$ 之间,还需要满足的是 $w^Tx$ 越大,则事件发生的几率越大,所以使用对数几率比即可:
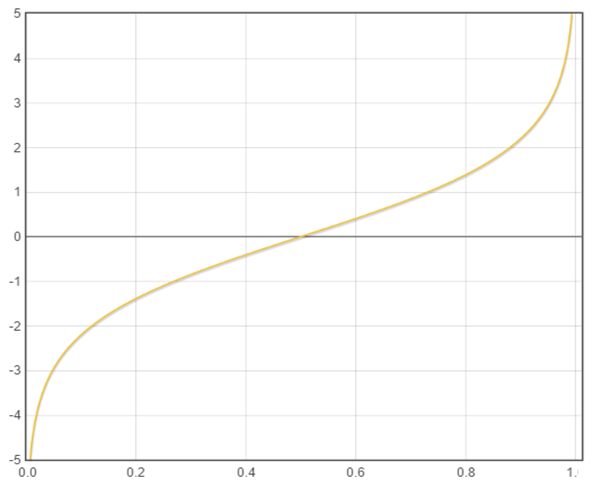
\[\log odds =\log \frac{z}{1-z}\]
\[\log \frac{z}{1- z} = w^Tx\]
综上便得到了 Logistic Regression 的模型, $z$ 便为模型的输出:
\[ z = \frac{e^{w^Tx}}{1+e^{w^Tx}} = \frac{1}{1+e^{-w^Tx}} \]
Generalized Liner Model 解释
从概率概率判别模型的角度来讲,Logistic Regression 是一种广义线性模型。所以需要注意给定自变量 $X$ 之后因变量 $Y$ 的条件期望值 $E(Y|X;w)$ 与变量 $X$ 之间的关系,这个对应关系便为所求解的模型,假设 $y \sim Bernoulli(z)$ ,同时 $y \sim ExponentialFamily(\eta)$,只需把 Bernoulli 化成 exponential family 的形式便可得到 $z$ 与 $\eta$ 的对应关系,这里直接给出结果,具体参考 广义线性模型 GLM :
\[ P(Y =1|X = x) = E[y|x;w] = z = \frac{1}{1+e^{-\eta}} = \frac{1}{1+e^{-w \cdot x}} \]
可见以上两种解释方式都得到了对 $x$ 的线性组合 $w^T \cdot x$ 做 sigmod 映射的形式,这边是模型的假设函数,接下来便可根据假设函数建立损失函数,并且进行参数估计与模型的求解.
参数估计
接下来需要对参数 $w$ 进行估计,方法很多,极大似然估计MLE ,负log损失或者叫做交叉熵损失,先看 MLE ,给定数据集 $\left\{(x_i,y_i)\right\}_{i=1}^N$ ,写出其似然函数 :
\[\prod_ip(y_i|x_i;z_i) = \prod_iz_i^{y_i}(1-z_i)^{1-y_i}\]
其中 $z_i = \frac{1}{1+e^{-w^T x_i}}$,转换为对数似然形式,最终只需极大化以下似然函数即可:
\[L(w) = \sum_iy_ilogz_i+(1-y_i)log(1-z_i)\]
这里来看另一种方法,即用负 log 损失函数来推导出 logistic 的损失函数,负log损失定义为: $L(y,P(Y|X)) = –logP(Y|X)$ ,根\[L(y,P(Y|X)) = \left\{ \begin{aligned}
-logP(Y=1|X=x), \ y=1 \\
-logP(Y=0|X=x), \ y = 0
\end{aligned}\right.\]据
$P(Y= 1| X=x) =z$ 与 $P(Y= 0| X =x) = 1-z$ 写成紧凑的形式:$L(y,z)=-ylogz-(1-y)log(1-z)$.
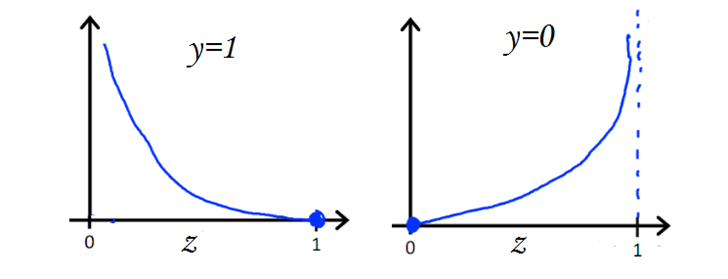
可以看到当$y = 1$时,$z$ 越接近 1 损失越小,当 $y = 0$ 时 , $z$ 越接近 1 损失越大,现在对于整个数据集可得:
\[ L(w) = -\sum_i[y_ilogz_i + (1-y_i)log(1-z_i)] \]
可见极大似然 MLE 正好等于极小化负 log 损失,因此两者是等价的,交叉熵在 2 分类下就是负 log 损失,所以交叉熵在 softmax 里会提到.
得到损失函数之后,为了防止过拟合,当然需要加上正则项了,这里以 $L_2$ 正则为例,加上正则后需要极小化的损失为:
\[ L(w) = –\sum_i[y_iz_i+(1-y_i)(1-z_i)]+ \frac{\lambda}{2}||w||^2\]
接下来直接使用梯度下降的来对 $w$ 进行更新:
\[w:= w – \frac{\partial L(w)}{\partial w}\]
这里对损失函数求导可以得到:
\begin{aligned}
\frac{\partial L(w) }{\partial w}& = \frac{\partial -\sum_i[y_ilogz_i+(1-y_i)log(1-z_i)] + \frac{\lambda}{2}||w||^2 }{ \partial w}\\
&=-\sum_i[y_i\frac{1}{z_i}+(1-y_i)\frac{1}{1-z_i}][z_i(1-z_i)]\frac{\partial w \cdot x_i}{ \partial w} +\lambda w \\
&= -\sum_i[y_i(1-z_i)-(1-y_i)z_i] \frac{\partial w \cdot x_i}{ \partial w}+ \lambda w \\
&= \sum_i(z_i -y_i) x_i + \lambda w \\
\end{aligned}
给出学习速率 $\alpha$ ,最终得到带有正则项的 Logistic Regression 回归的梯度下降算法:
$while$ $iter < iter\_num$ $do$ :
\[w:= w – \alpha \left [\sum_i(z_i -y_i) x_i +\lambda w \right ]\]
Softmax Regression
Softmax Regression 即为一个 K 分类的概率判别模型,就是把 Logistic Regression 推广到 K 分类的版本,把样本 $x$ 属于类别 $k$ 的概率用 $z_k$ 表示,即 $z_k = P(Y = k| X = x)$ ,可以得到 Softmax 的假设函数如下:
\[\left[ \begin{aligned}z_1 \\z_2 \\ ...\\z_K \end{aligned}\right]=\frac{1}{\sum_{j=1}^Ke^{w_j^Tx}}\left[ \begin{aligned}e^{w_1^Tx} \\e^{w_2^Tx} \\ ...\\e^{w_K^Tx} \end{aligned}\right]\]
建立 Softmax 模型的步骤是给定训练数据集 $\left\{(x_i,y_i)\right\}_{i=1}^N$ ,这里 $y_i \in \mathbb{R}^K$ ,假设 $x_i$ 属于类别 $k$ ,则 $y_i$ 的第 $k$ 维为 1 ,其余维度为 0 。Softmax 其实就是 Logistic 的多分类的推广,这里的变量 $Y$ 是服从多项分布的,所以可以通过多项分布极大似然的方式来推导出 Softmax 。
Softmax 参数估计
首先来个单个样本的损失,对于单个服从多项分布的样本,其似然函数为 $\prod_kz_k^{y_k}$ , 极大化该似然函数正好等于极小化以下交叉熵损失:
\[L(w) = -\sum_k y_k \log z_k \]
\[z_k = \frac{e^{w_k^Tx}}{\sum_je^{w_j^Tx}}\]
这里同样需要对损失函数 $L(W)$ 求导,注意这里 $W$ 采用大写,是因为 $W$ 为矩阵,其形式为 $[w_1,w_2,…,w_K]$,因为每个类别需要一组参数,求导前要明确 $z_k$ 对 $w_i$ 与 $w_k$ 的导数:
\begin{aligned}
\frac{\partial z_{k} }{\partial w_i} &= -y_k \cdot y_i \\
\frac{\partial z_{k} }{\partial w_k} &= y_k \cdot (1-y_k) \\
\end{aligned}
这里代表对 $w_k$ 求导代表 $i =k$ 时求导;对 $w_i$ 求导代表对 $i \ne k$ 求导,两个结果是不一样的。首先是 $z_k$ 对 $w_k$ 的导数:
\begin{aligned}
\frac{\partial z_{k} }{\partial w_k} &= \frac{\partial }{\partial w_k}\left ( \frac{e^{w_{k}x}}{\sum_je^{ w_{j}x} }\right) \\
&= [e^{w_{k}x}]_{w_k'}\frac{1}{\sum_je^{ w_{j}x} }+e^{w_{k}x}\left [\frac{1}{\sum_je^{ w_{j}x} } \right ]_{w_k'}\\
&= \frac{\partial w_kx}{\partial w_k}\frac{e^{w_{k}x}}{\sum_je^{ w_{j}x} }-e^{w_{k}x}\frac{e^{w_{k}x}}{\left (\sum_je^{ w_{j}x} \right )^2}\frac{\partial w_kx}{\partial w_k}\\
&=\frac{e^{w_{k}x}}{\sum_je^{ w_{j}x} } \cdot x - \left (\frac{e^{w_{k}x}}{\sum_je^{ w_{j}x} }\right )^2 \cdot x \\
&= z_k(1-z_k)\cdot x
\end{aligned}接下来是 $z_k$ 对 $w_i$ 的导数:
\begin{aligned}
\frac{\partial z_{k} }{\partial w_i}
&= \frac{\partial }{\partial w_i}\left ( \frac{e^{w_{k}x}}{\sum_je^{ w_{j}x} }\right) \\
&= -\frac{e^{w_{k}x}}{\left ( \sum_je^{ w_{j}x} \right)^2 } \frac{\partial \sum_je^{ w_{j}x} }{\partial w_i} \\
&=-\frac{e^{w_{k}x} }{\sum_je^{ w_{j}x} } \cdot \frac{ e^{w_{i}x} }{ \sum_je^{ w_{j}x} }\cdot \frac{\partial w_ix}{\partial w_i} \\
&=-z_k z_i \cdot x
\end{aligned}
因此单个样本损失函数对权重 $w_j$ 求损失,可得:
\begin{aligned}
\frac{\partial \left [-\sum_k y_k \log z_k \right ] }{\partial w_j} &= -\sum_ky_k \cdot \frac{\partial \log z_k}{\partial w_j} \\
&= -\sum_ky_k \frac{1}{z_k} \frac{\partial z_k}{\partial w_j} \\
&= -y_j\frac{1}{z_j}z_j(1-z_j)x - \sum_{k \ne j} y_k \frac{1}{z_k}(-z_j z_k)x \\
&= \left (-y_j +y_jz_j+ \sum_{k \ne j} y_kz_j \right ) \cdot x \\
&= \left (-y_j + z_j\sum_ky_k \right )\cdot x \\
&=\left (z_j-y_j \right )\cdot x
\end{aligned}
得到单个样本的导数之后,接下来结算对于整个训练集 $\left \{(x_i,y_i) \right \}_{i=1}^N$ 的导数,这里记 $y_{ik}$ 为第 $i$ 个样本标签向量的第 $k$ 维度;$z_{ik}$ 代表样本 $x_i$ 属于类别 $k$ 的概率,即 $z_{ik} = P(Y= k | X=x_i)$ ,终可得带有 $L_2$ 正则的损失函数为:
\[L(W) = -\sum_i\sum_k y_{ik} \log z_{ik} + \frac{1}{2} \lambda ||W||^2\]
接下来对权重 $w_k$ 求导,可得:
\[ \frac{\partial L(W)}{\partial w_k} = \sum_i ( z_{ik}- y_{ik})x_i + \lambda w_k \]
综上,给出带有 $L_2$ 正则的 Softmax Regression 的算法:
$while$ $iter < iter\_num$ $do$:
$for$ $k=1 …K$:
\[ w_k := w_k -\sum_i (z_{ik} -y_{ik}) \cdot x_i + \lambda w_k \]
并行化 Logistic
工业界使用 Logistic 一般都是大规模数据,超级高的维度,所以有必要对 Logistic 进行并行化处理,以下给出三种并行方式:
1) data parallelism ,适用于维度适中的样本,分别把数据发送到各个节点,每个节点运行各自的 SGD ,等所有节点运行完成后将结果取平均汇总,若没达到收敛条件,则进行下一次迭代,伪代码如下:

2) data parallelism ,数据分发到各个节点,并获取当前时刻最新的参数 $\theta^t$ ,各个计算完 $\Delta \theta$ 之后(下图中的 $temp^{(i)}$ ),将 $\Delta \theta$ 汇总,用于计算 $\theta^{t+1} = \theta^t - \alpha \sum \Delta \theta$,伪码如下:
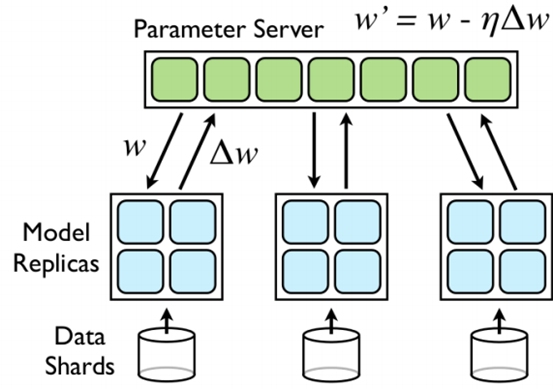
3)将 data parallelism 与 model parallelism 结合,因为 Logistic Regression 中特征的维度通常很高,单机不一定能完成梯度计算,所以有了 Google 实现了一个 DistBelief ,采用 Parameter Server 来同步参数,异步运行,速度杠杠的,这里的 Model Replicas 是一个 Logistic Regression 模型,由几个计算节点组成,如下图所示:
模型的几个主要特点,以下这些特点虽然有些缺乏理论基础,但最后得到的模型效果是相当好的:
1)通过一个共享的 Parameter Server 来共享参数,每次处理一个 Mini-Batch 之前,从 Parameter Server 获取当前的参数 $w$,求得其导数 $\Delta w$ ,并推送到 Parameter Server 进行更新;
2) Model Replicas 是异步执行的,所以省去了同步的时间;
3)每 $n_{fetch}$ 次Mini-Batch 向服务器取一次参数,每 $n_{push}$ 次 Mini –Batch 操作推送一次结果, $n_{fetch}$ 不一定等于 $n_{push}$;
4)一个 Model Replicas 失效,其他的 Model Replicas 仍可以运行,所以鲁棒性很强;
5)每个 Model Replicas 中的节点只需和 Parameter Server 中和该节点有关的模型参数的那部分节点进行通信;
6)每个 Model Replicas 中的 fetch compute push 操作是通过三个线程完成的,类似于流水线机制,大大加快了速度;
7)参数服务器的每个节点更新参数的次数不一定相同,有一定的随机性.
总结
基础好不够扎实,缺乏实践经验,对 MaxEnt 与 Logistic 的关系 与 GLM 理解的不够好,暂时告一段落.有机会继续深入.
参考文献:
Google paper: Large Scale Distributed Deep Networks
书籍: PRML ,MLAPP,统计学习方法
http://tech.meituan.com/intro_to_logistic_regression.html 有一个应用可以参考一下
http://www.cnblogs.com/ooon/p/5577241.html
http://www.cnblogs.com/ooon/p/5340071.html
http://www.cnblogs.com/ooon/p/4934413.html
http://www.cuishilin.com/2015/10/206.html 为什么选用 sigmod 和最大熵的关系
http://fibears.top/2016/04/08/LRModel/
http://blog.csdn.net/buring_/article/details/43342341 softmax 与 maxent 的等价证明



 浙公网安备 33010602011771号
浙公网安备 33010602011771号