（六）6.17 Neurons Networks convolutional neural network（cnn）

之前所讲的图像处理都是小 patchs ，比如28*28或者36*36之类，考虑如下情形，对于一副1000*1000的图像，即10⁶，当隐层也有10⁶节点时，那么W⁽¹⁾的数量将达到10¹²级别，为了减少参数规模，加快训练速度，CNN应运而生。CNN就像辟邪剑谱一样，正常人练得很挫，一旦自宫后，就变得很厉害。CNN有几个重要的点：局部感知、参数共享、池化。

 局部感知

局部感知野。一般认为人对外界的认知是从局部到全局的，而图像的空间联系也是局部的像素联系较为紧密，而距离较远的像素相关性则较弱。因而，每个神经元其实没有必要对全局图像进行感知，只需要对局部进行感知，然后在更高层将局部的信息综合起来就得到了全局的信息。每个隐含单元仅仅连接输入单元的一部分。例如，每个隐含单元仅仅连接输入图像的一小片相邻区域。对于一个输入与隐层均有 $10^6$ 的网络，假设每个隐含单元只与 10*10 的输入区域相连接，这时参数的个数变为 $10 \times 10 \times  $10^6= 10^8$，降低了$10^4$ 个数量级，这样训练起来就没有那么费力了。这一思想主要受启发于生物学里面的视觉系统结构。视觉皮层的神经元就是局部接受信息的（即这些神经元只响应某些特定区域的刺激）,此外图像的像素也是局部时空相关的。

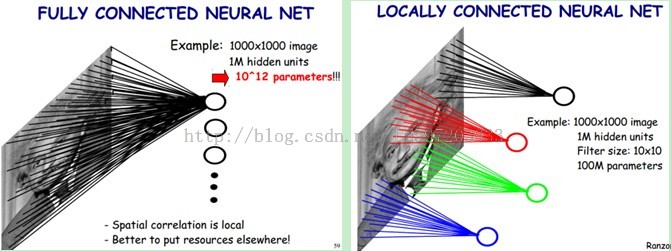
如下图所示，左边就是全连接网络，每个隐藏神经元与每个像素进行连接。右边就是部分连接网络，每个隐神经元只与一部分区域相连接。右边的图进行的便是卷积操作，该操作会生成一副 feature map 。

 参数共享

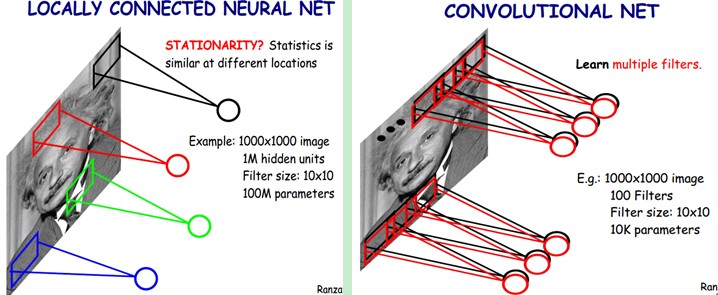
尽管减少了几个数量级，但参数数量依然较多。能不能再进一步减少呢？能！方法就是权值共享。具体做法是，在局部连接中隐藏层的每一个神经元连接的是一个 10×10 的局部图像，因此有10×10 个权值参数，将这 10×10 个权值参数共享给剩下的神经元，也就是说隐藏层中 $10^6$ 个神经元的权值参数相同，那么此时不管隐藏层神经元的数目是多少，需要训练的参数就是这 10×10 个权值参数（也就是卷积核(也称滤波器)的大小），如下图。这样来参数真的是极大的简化了啊！这个思想主要来源于：自然图像有其固有特性，也就是说，图像的一部分的统计特性与其他部分是一样的。这也意味着我们在这一部分学习的特征也能用在另一部分上，所以对于这个图像上的所有位置，我们都能使用同样的学习特征。

单核单通道卷积

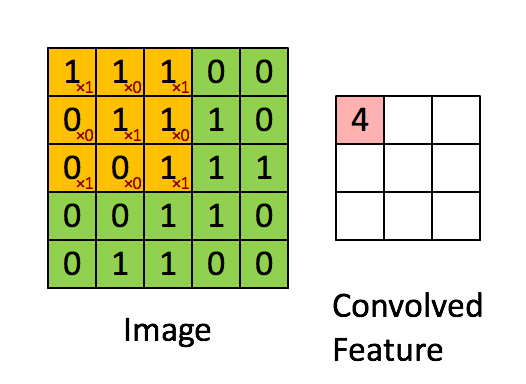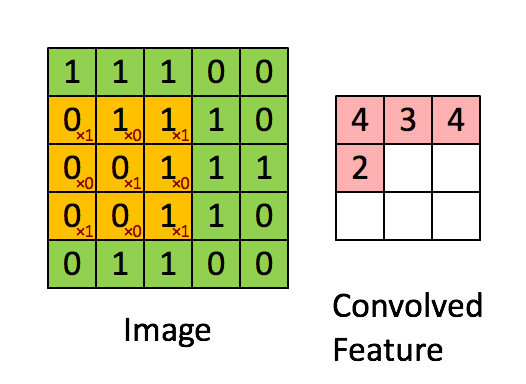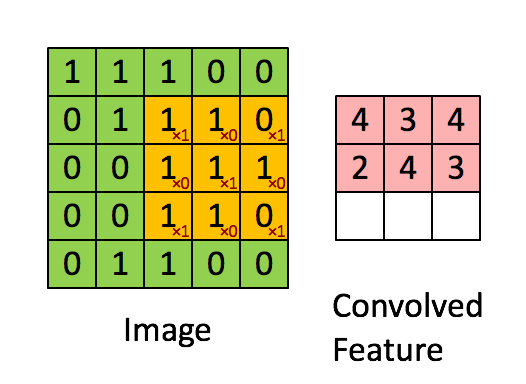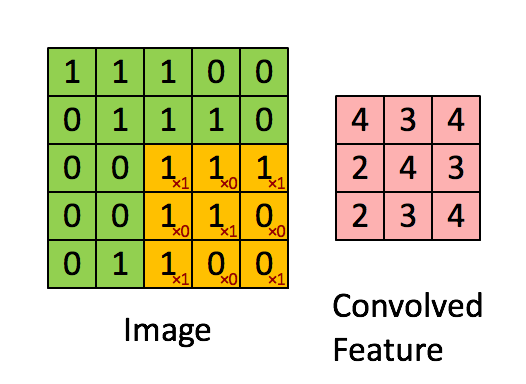
如果隐神经元与其连接的100个输入单元具有相同的100个参数，那么就相当于是一个 10*10 的模板在原始的输入图像上做卷积(当然需要加上一个偏置参数b)，这样相当于得到一个新的图像，新图像的大小为(1000-100+1)*(1000-100+1),因此也得名卷积神经网络。这样的10*10的模板，我们也把它称为一个卷积核。以下为单个卷积核示意图：

多核单通道卷积

CNN中只用一个卷积核提取得到的特征往往是不充分的，只能算作是一种类型的特征(比如某个方向的边缘)，如果我们要提取其它方向的边缘，那就多弄几个卷积核，这样就变成了多卷积核了。假设有k个卷积核，那么可训练的参数的个数就变为了k×10×10。注意没有包含偏置参数。每个卷积核得到一副特征图像也被称为一个Feature Map。卷积的过程也被称为特征提取的过程，多核卷积中，隐层的节点数量为： k×(1000-100+1)×(1000-100+1) ，对于下图的手写数字灰度图，做单通道卷及操作：

多核多通道卷积

当图像为RGB或ARGB（A代表透明度）时，可以在多通道进行卷积操作，或者对于堆叠卷积层来说， pooling 层之后可以继续接下一个 卷积层，对 pooling 层多个 Feature Map 的操作即为多通道卷积，下图为 $w_1,w_2$ 两个卷积核在ARGB四通道上进行卷积操作，在生成 $w_1$ 对应的 Feature Map 时，$w_1$ 这个卷积核对应4个卷积模板，分别用4种不同的颜色表示，Feature Map 对应的位置的值是由四核卷积模板分别作用在4个通道的对应位置处的卷积结果相加然后取激活函数得到的，所以在四通道得到2通道的过程中，参数数目为 4×2×2×2个，其中4表示4个通道，第一个2表示生成2个通道，最后的2×2表示卷积核大小。见下图：

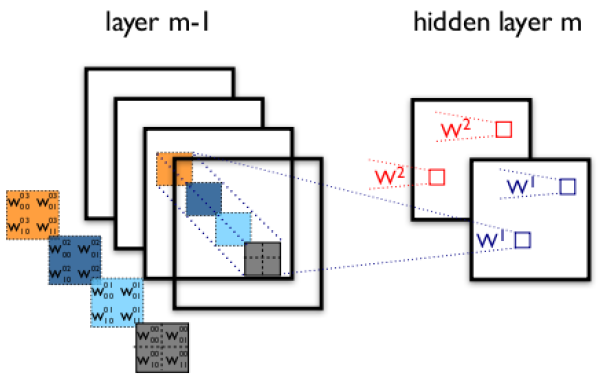
池化 pooling

通过卷积操作获得了特征 (features) 之后，下一步我们要利用这些特征去做分类。可以用所有提取得到的特征去训练分类器，例如用这些特征训练一个 softmax 分类器，对于一个 96X96 像素的图像，假设我们已经学习得到了400个 Feature Map，每个 Feature Map 都定义在 8X8 卷积核上，每一个卷积核和图像卷积都会得到一个 (96 − 8 + 1) * (96 − 8 + 1) = 7921 维的卷积特征，由于有 400 个Feature Map，所以每个训练样例(输入图像) 都会得到一个 7921* 400 = 3,168,400 维的卷积特征向量。学习一个拥有超过 3 百万特征输入的分类器十分不便，并且容易出现过拟合 (over-fitting)。

为了解决这个问题，首先回忆一下，之所以决定使用卷积后的特征是因为图像具有一种“静态性”的属性，这也就意味着在一个图像区域有用的特征极有可能在另一个区域同样适用。因此，处理大图像时，一个很自然的想法就是对不同位置的特征进行聚合统计，比如可以计算图像一个区域上的某个特定特征的平均值 (或最大值)。这些概要统计特征不仅具有低得多的维度 (相比使用所有提取得到的特征)，同时还会改善结果(不容易过拟合)。这种聚合的操作就叫做池化 (pooling)，有时也称为平均池化或者最大池化 (取决于计算池化的方法)。池化的过程通常也被称为特征映射的过程，如下图过程如下所示：

CNN的应用

下面来看 LeNet-5 ，用于实现手写识别的7层CNN（不包含输入层），以下为LeNet-5的示意图：

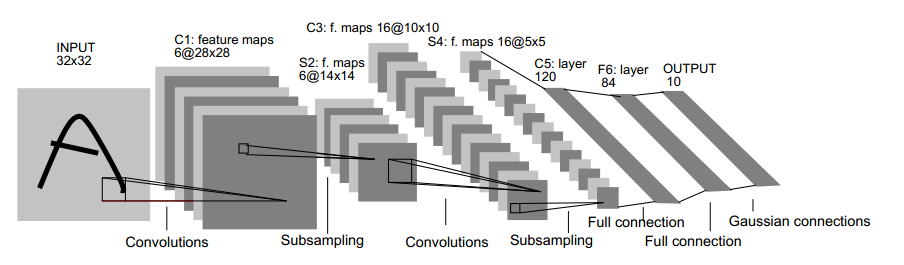
输入原始图像的大小是32×32，卷积层用 $C_x$ 表示，子采样层（pooling）用$S_x$表示，全连接层用$F_x$表示，x 代表层数。

         C1层是卷积层，单通道下用了6个卷积核，这样就得到了6个feature map，其中每个卷积核的大小为5*5，用每个卷积核与原始的输入图像进行卷积，这样feature map的大小为(32-5+1)×(32-5+1)= 28×28，所需要的参数的个数为(5×5+1)×6= 156(其中5×5为卷积模板参数，1为偏置参数)，连接数为(5×5+1)×28×28×6=122304(其中28×28为卷积后图像的大小)。

         S2层为 pooling 层，也可以说是池化或者特征映射的过程，拥有6个 feature map，每个feature map的大小为14*14，每个feature map的隐单元与上一层C1相对应的feature map的 2×2 单元相连接，这里没有重叠。计算过程是：2×2 单元里的值相加然后再乘以训练参数w，再加上一个偏置参数b(每一个feature map共享相同w和b)，然后取sigmoid 值，作为对应的该单元的值。所以S2层中每 feature map 的长宽都是上一层C1的一半。S2层需要2×6=12个参数，连接数为(4+1)×14×14×6 = 5880。注：这里池化的过程与ufldl教程中略有不同。下面为卷积操作与池化的示意图：

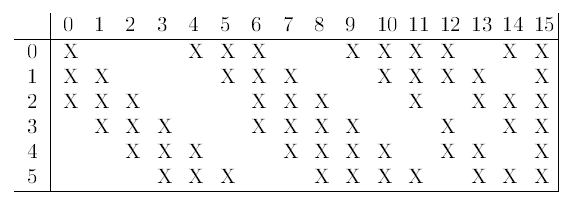
         C3层也是一个卷积层（多通道16核卷积，注意此处C3并不是与S2全连接而是部分连接，见下图），有16个卷积核，卷积模板的大小为5*5，因此具有16个feature maps，每个feature map的大小为(14-5+1×(14-5+1）= 10×10。每个feature map只与上一层S2中部分feature maps相连接，下表给出了16个feature maps与上一层S2的连接方式(行为S2层feature map的标号，列为C3层feature map的标号，第一列表示C3层的第0个feature map只有S2层的第0、1和2这三个feature maps相连接，其它解释类似)。为什么要采用部分连接，而不采用全连接呢？首先就是部分连接，可计算的参数就会比较少，其次更重要的是它能打破对称性，这样就能得到输入的不同特征集合。以第0个feature map描述计算过程：用1个卷积核(对应3个卷积模板，但仍称为一个卷积核，可以认为是三维卷积核)分别与S2层的3个feature maps进行卷积，然后将卷积的结果相加，再加上一个偏置，再取sigmoid就可以得出对应的feature map了。所需要的参数数目为（5×5×3+1)×6 +(5×5×4+1)×9 +5×5×6+1 = 1516(5×5为卷积参数，卷积核分别有 3 4 6 个卷积模板)，连接数为1516*10*10= 151600 (98论文年论文给出的结果是156000，个人认为这是错误的，因为一个卷积核只有一个偏置参数 ？)。

         S4层也是采样层，有16个feature maps，每个feature map的大小为5×5，计算过程和S2类似，需要参数个数为16×2 = 32个，连接数为(4+1)×5×5×16 = 2000.

         C5为卷积层，有120个卷积核，卷积核的大小仍然为5×5，因此有120个feature maps，每个feature map的大小都与上一层S4的所有feature maps进行连接，这样一个卷积核就有16个卷积模板。Feature map的大小为1×1，这样刚好变成了全连接，但是我们不把它写成F5，因为这只是巧合。C5层有120*(5*5*16+1) = 48120(16为上一层所有的feature maps个数)参数，连接数也是这么多。

         F6层有86个神经单元，每个神经单元与C5进行全连接。它的连接数和参数均为 86 × 120 = 10164 。这样F6层就可以得到一个86维特征了。后面可以使用该86维特征进行做分类预测等内容了。注意：这里卷积和池化的计算过程和ufldl教程中的计算略有不同。

 

参考：

1：UFLDL：http://deeplearning.stanford.edu/wiki/index.php/UFLDL_Tutorial

2：论文：Gradient-BasedLearning Applied to Document Recognition

3：http://blog.csdn.net/stdcoutzyx/article/details/41596663

4：http://blog.csdn.net/lu597203933/article/details/46575779