(六)6.4 Neurons Networks Autoencoders and Sparsity
BP算法是适合监督学习的,因为要计算损失函数,计算时y值又是必不可少的,现在假设有一系列的无标签train data: 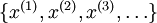 ,其中
,其中 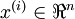 ,autoencoders是一种无监督学习算法,它使用了本身作为标签以此来使用BP算法进行训练,即
,autoencoders是一种无监督学习算法,它使用了本身作为标签以此来使用BP算法进行训练,即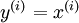 ,见如下示例:
,见如下示例:
自编码器尝试学习一个 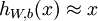 的函数,它尝试逼近一个恒等函数,从而使得输出
的函数,它尝试逼近一个恒等函数,从而使得输出 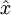 接近于输入
接近于输入  ,这样做的意义在于如果对hidden layer加上一些限制,比如hidden layer的数量限制,就可以从输入数据中发现一些有趣的结构。
,这样做的意义在于如果对hidden layer加上一些限制,比如hidden layer的数量限制,就可以从输入数据中发现一些有趣的结构。
举个栗子:假设网络的输入 是一张
是一张 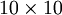 的灰度图像(共100个像素),即input layer 有100个单元,设置 hidden layer有50个单元,且对output layer有
的灰度图像(共100个像素),即input layer 有100个单元,设置 hidden layer有50个单元,且对output layer有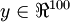 ,这样就会迫使网络学习图像的压缩表示,因为要从这50个隐藏单元中重构出输入的
,这样就会迫使网络学习图像的压缩表示,因为要从这50个隐藏单元中重构出输入的 ,如果输入数据x是完全随机的,即每个
,如果输入数据x是完全随机的,即每个 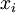 都是一个跟其它特征完全无关的独立同分布高斯随机变量,那么这一压缩表示将会非常难学习。当某些特征之间彼此相关时,那么这一算法就可以发现输入数据中的这些相关性。事实上,这一简单的自编码神经网络通常可以学习出一个跟PCA结果非常相似的输入数据的低维表示。
都是一个跟其它特征完全无关的独立同分布高斯随机变量,那么这一压缩表示将会非常难学习。当某些特征之间彼此相关时,那么这一算法就可以发现输入数据中的这些相关性。事实上,这一简单的自编码神经网络通常可以学习出一个跟PCA结果非常相似的输入数据的低维表示。
以上是隐藏层单元很少的情况,当隐层有很多的单元时(可能多于输入层),仍可以对网络施加一些限制来发现输入数据的结构,比如给网络加上稀疏性限制(假设神经元的激活函数是sigmod函数)稀疏性简单来说就是当网络中某个单元的输出接近1的时候就认为他被激活,而输出接近0的时候则认为他被抑制,那么使得神经元大部分情况下都被抑制的情况称作稀疏性限制,如果使用tanh作为激活函数的话,当神经元输出为-1的时候,我们认为神经元是被抑制的。
三层网络下用 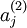 表示隐层神经元
表示隐层神经元  的激活度,对于给定的输入
的激活度,对于给定的输入  ,使用
,使用 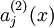 代表给定的输入为
代表给定的输入为  的情况下,自编码神经网络隐藏神经元
的情况下,自编码神经网络隐藏神经元  的激活度。进一步有
的激活度。进一步有
![\begin{align}
\hat\rho_j = \frac{1}{m} \sum_{i=1}^m \left[ a^{(2)}_j(x^{(i)}) \right]
\end{align}](http://ufldl.stanford.edu/wiki/images/math/8/7/2/8728009d101b17918c7ef40a6b1d34bb.png) ,
,
其中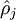 表示隐藏神经元
表示隐藏神经元  的平均活跃度(在训练集上取平均)。我们可以近似的加入一条限制
的平均活跃度(在训练集上取平均)。我们可以近似的加入一条限制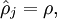 ,其中,
,其中, 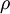 是稀疏性参数,通常是一个接近于0的较小的值(比如
是稀疏性参数,通常是一个接近于0的较小的值(比如 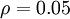 )。换句话说,想让隐藏神经元
)。换句话说,想让隐藏神经元  的平均活跃度接近0.05,隐藏神经元的活跃度必须尽可能接近0才能使
的平均活跃度接近0.05,隐藏神经元的活跃度必须尽可能接近0才能使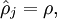 =0.05。
=0.05。
想满足这一限制,在原有的损失函数中加入额外的惩罚因子,惩罚那些 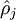 和
和 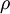 有显著不同的情况,进而使隐层的平均激活度尽可能的 =
有显著不同的情况,进而使隐层的平均激活度尽可能的 = 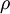 ,惩罚因子的选择很多,本文如下:
,惩罚因子的选择很多,本文如下:
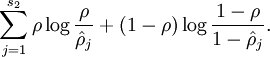
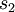 是隐藏层中隐藏神经元的数量,而索引
是隐藏层中隐藏神经元的数量,而索引  依次代表隐藏层中的每一个神经元。这其实是相对熵,,可以表示如下:
依次代表隐藏层中的每一个神经元。这其实是相对熵,,可以表示如下:
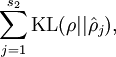
因为 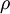 和
和 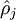 均可以看做服从伯努利, 所以
均可以看做服从伯努利, 所以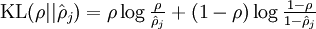 是一个以
是一个以 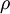 为均值和一个以
为均值和一个以 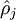 为均值的两个伯努利随机变量之间的相对熵。相对熵是一种标准的用来测量两个分布之间差异的方法。
为均值的两个伯努利随机变量之间的相对熵。相对熵是一种标准的用来测量两个分布之间差异的方法。
这一惩罚因子有如下性质,当 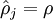 时
时 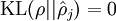 ,并且随着
,并且随着 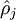 与
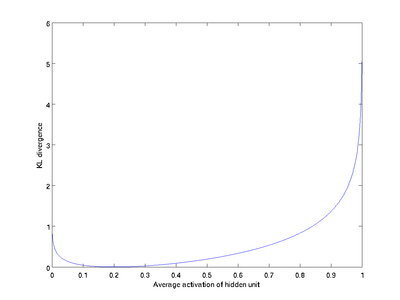
与 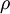 之间的差异增大而单调递增。所以应尽量让KL离散度变小,才能满足稀疏限制,举例来说,在下图中,我们设定
之间的差异增大而单调递增。所以应尽量让KL离散度变小,才能满足稀疏限制,举例来说,在下图中,我们设定 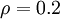 并且画出了相对熵值
并且画出了相对熵值 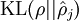 随着
随着 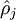 变化的变化。
变化的变化。
我们可以看出,相对熵在 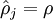 时达到它的最小值0,而当
时达到它的最小值0,而当 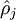 靠近0或者1的时候,相对熵则变得非常大(其实是趋向于
靠近0或者1的时候,相对熵则变得非常大(其实是趋向于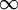 )。所以,最小化这一惩罚因子具有使得
)。所以,最小化这一惩罚因子具有使得 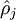 靠近
靠近 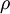 的效果。 现在,我们的总体代价函数可以表示为
的效果。 现在,我们的总体代价函数可以表示为
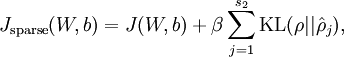
其中 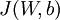 如之前所定义,而
如之前所定义,而 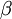 控制稀疏性惩罚因子的权重。
控制稀疏性惩罚因子的权重。 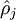 项则也(间接地)取决于
项则也(间接地)取决于 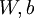 ,因为它是隐藏神经元
,因为它是隐藏神经元  的平均激活度,而隐藏层神经元的激活度取决于
的平均激活度,而隐藏层神经元的激活度取决于 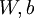 。
。
此处因为损失函数的改动,需要重新计算BP算法中残差项:
由原来的:
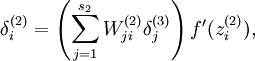
现在我们将其换成
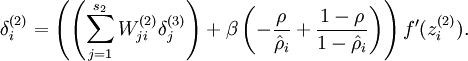
系数项推倒:
对于单个样本稀疏项是关于W(1) b(1)的函数

根据链式求导法则有:

所以单个样本系数项关于参数W(1) b(1)的倒数为:

与J(W,b)合并之后有JSparse(W,b):

其中i代表第二层,j代表第一层,r代表第三层,中间部分即为残差公式。
如上公式,计算残差时需要知道 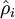 。所以在计算后向传播之前,需要对所有的训练样本计算一遍前向传播,从而获取平均激活度。如果训练样本可以整个存到内存之中(对于编程作业来说,通常如此),便可以方便地在所有的样本上计算前向传播并将得到的激活度存入内存并且计算平均激活度 。然后就可以使用事先计算好的激活度来对所有的训练样本进行后向传播的计算。如果数据量太大,无法全部存入内存,就可以扫过训练样本并计算一次前向传播,然后将获得的结果累积起来并计算平均激活度
。所以在计算后向传播之前,需要对所有的训练样本计算一遍前向传播,从而获取平均激活度。如果训练样本可以整个存到内存之中(对于编程作业来说,通常如此),便可以方便地在所有的样本上计算前向传播并将得到的激活度存入内存并且计算平均激活度 。然后就可以使用事先计算好的激活度来对所有的训练样本进行后向传播的计算。如果数据量太大,无法全部存入内存,就可以扫过训练样本并计算一次前向传播,然后将获得的结果累积起来并计算平均激活度 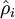 (当某一个前向传播的结果中的激活度
(当某一个前向传播的结果中的激活度 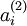 被用于计算平均激活度
被用于计算平均激活度 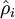 之后就可以将此结果删除)。然后当完成平均激活度
之后就可以将此结果删除)。然后当完成平均激活度 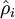 的计算之后,需要重新对每一个训练样本做一次前向传播从而可以对其进行后向传播的计算。对于后一种情况,对每一个训练样本需要计算两次前向传播,所以在计算上的效率会稍低一些。
的计算之后,需要重新对每一个训练样本做一次前向传播从而可以对其进行后向传播的计算。对于后一种情况,对每一个训练样本需要计算两次前向传播,所以在计算上的效率会稍低一些。
如果想要使用经过以上修改的后向传播来实现自编码神经网络,那么就会对目标函数 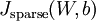 做梯度下降。使用梯度验证方法确保其准确性即可。
做梯度下降。使用梯度验证方法确保其准确性即可。
训练完(稀疏)自编码器之后,可以把学到的函数可视化出来,对于训练10*10的图像,每个隐藏单元进行如下计算:
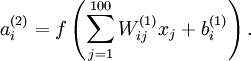
将要可视化的就是上面这个以2D图像为输入,由隐藏单元i计算出来的结果。它是依赖于参数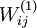 的(暂时忽略偏置项bi),
的(暂时忽略偏置项bi),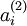 可看作输入
可看作输入 的非线性特征,存在一个问题,什么样的输入图像
的非线性特征,存在一个问题,什么样的输入图像 可让
可让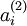 得到最大程度的激励?(通俗一点说,隐藏单元
得到最大程度的激励?(通俗一点说,隐藏单元 要找个什么样的特征?),若假设输入有范数约束
要找个什么样的特征?),若假设输入有范数约束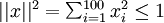 ,则令隐藏单元
,则令隐藏单元 得到最大激励的输入应由下面公式计算的像素
得到最大激励的输入应由下面公式计算的像素 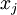 给出(共需计算100个像素,j=1,…,100):
给出(共需计算100个像素,j=1,…,100):
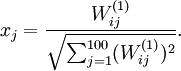
当用上式算出各像素的值、把它们组成一幅图像、并将图像呈现出来,隐藏单元  所寻找的特征的真正含义也渐渐明朗起来。
所寻找的特征的真正含义也渐渐明朗起来。
假如训练的自编码器有100个隐藏单元,可视化结果就会包含100幅这样的图像——每个隐藏单元都对应一幅图像。由这100幅图像可以看出隐藏单元学出来的整体效果如何,当对稀疏自编码器(100个隐藏单元,在10X10像素的输入上训练 )进行上述可视化处理之后,结果如下所示:
上图的每个小方块都给出了一个(带有有界范数 的)输入图像 ,它可使这100个隐藏单元中的某一个获得最大激励。我们可以看到,不同的隐藏单元学会了在图像的不同位置和方向进行边缘检测。
,它可使这100个隐藏单元中的某一个获得最大激励。我们可以看到,不同的隐藏单元学会了在图像的不同位置和方向进行边缘检测。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号