(六) 6.3 Neurons Networks Gradient Checking

BP算法很难调试，一般情况下会隐隐存在一些小问题，比如（off-by-one error），即只有部分层的权重得到训练，或者忘记计算bais unit，这虽然会得到一个正确的结果，但效果差于准确BP得到的结果。

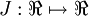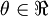有了cost function，目标是求出一组参数W，b，这里以\textstyle \theta表示，cost function 暂且记做\textstyle J(\theta)。假设 \textstyle J : \Re \mapsto \Re，则 \textstyle \theta \in \Re，即一维情况下的Gradient Descent:

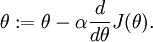
\begin{align} \theta := \theta - \alpha \frac{d}{d\theta}J(\theta). \end{align}

根据6.2中对单个参数单个样本的求导公式：

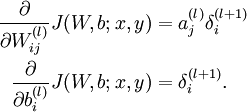
\begin{align} \frac{\partial}{\partial W_{ij}^{(l)}} J(W,b; x, y) &= a^{(l)}_j \delta_i^{(l+1)} \\ \frac{\partial}{\partial b_{i}^{(l)}} J(W,b; x, y) &= \delta_i^{(l+1)}. \end{align}

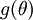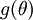可以得到每个参数的偏导数，对所有样本累计求和，可以得到所有训练数据对参数 \textstyle \theta 的偏导数记做 \textstyle g(\theta) ，\textstyle g(\theta) 是靠BP算法求得的，为了验证其正确性，看下图回忆导数公式：

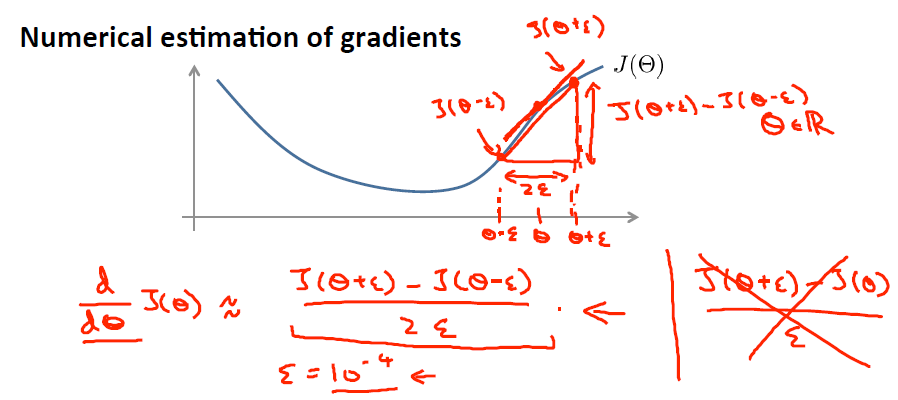
可见有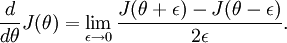：\begin{align} \frac{d}{d\theta}J(\theta) = \lim_{\epsilon \rightarrow 0} \frac{J(\theta+ \epsilon) - J(\theta-\epsilon)}{2 \epsilon}. \end{align}那么对于任意 \textstyle \theta 值，我们都可以对等式左边的导数用：

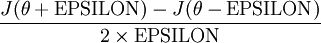\begin{align} \frac{J(\theta+{\rm EPSILON}) - J(\theta-{\rm EPSILON})}{2 \times {\rm EPSILON}} \end{align}来近似。

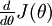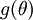给定一个被认为能计算 \textstyle \frac{d}{d\theta}J(\theta) 的函数\textstyle g(\theta)，可以用下面的数值检验公式

\begin{align} g(\theta) \approx \frac{J(\theta+{\rm EPSILON}) - J(\theta-{\rm EPSILON})}{2 \times {\rm EPSILON}}. \end{align}

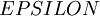应用时，通常把\textstyle EPSILON设置为一个很小的常量，比如在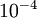\textstyle 10^{-4} 数量级，最好不要太小了，会造成数值的舍入误差。上式两端值的接近程度取决于 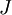\textstyle J 的具体形式。假定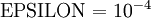\textstyle {\rm EPSILON} = 10^{-4} 的情况下，上式左右两端至少有4位有效数字是一样的（通常会更多）。

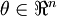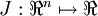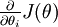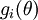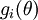当\textstyle \theta \in \Re^n是一个n维向量而不是实数时，且 \textstyle J: \Re^n \mapsto \Re，在 Neorons Network 中，J（W，b）可以想象为 W，b 组合扩展而成的一个长向量 \textstyle \theta，现在又一个计算 \textstyle \frac{\partial}{\partial \theta_i} J(\theta)的函数 \textstyle g_i(\theta)，如何检验\textstyle g_i(\theta)能否输出到正确结果呢，用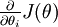\textstyle \frac{\partial}{\partial \theta_i} J(\theta)的取值来检验，对于向量的偏导数：

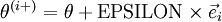根据上图，对 \textstyle \thetai 求导时，只需要在向量的第i维上进行加减操作，然后求值即可，定义 \textstyle \theta^{(i+)} = \theta + {\rm EPSILON} \times \vec{e}_i，其中

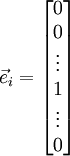
\begin{align} \vec{e}_i = \begin{bmatrix}0 \\ 0 \\ \vdots \\ 1 \\ \vdots \\ 0\end{bmatrix} \end{align}

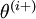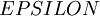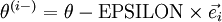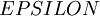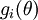\textstyle \theta^{(i+)} 和 \textstyle \theta 几乎相同，除了第 \textstyle i 行元素增加了 \textstyle EPSILON，类似地，\textstyle \theta^{(i-)} = \theta - {\rm EPSILON} \times \vec{e}_i 得到的第 \textstyle i 行减小了 \textstyle EPSILON，然后求导并与\textstyle g_i(\theta)比较：

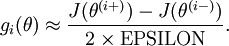
\begin{align} g_i(\theta) \approx \frac{J(\theta^{(i+)}) - J(\theta^{(i-)})}{2 \times {\rm EPSILON}}. \end{align}

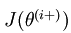中的参数对应的是参数向量中一个分量的细微变化，损失函数J 在不同情况下会有不同的值（比如三层NN 或者 三层autoencoder（需加上稀疏项）），上式中左边为BP算法的结果，右边为真正的梯度，只要两者很接近，说明BP算法是在正确工作，对于梯度下降中的参数是按照如下方式进行更新的：

\begin{align} W^{(l)} &= W^{(l)} - \alpha \left[ \left(\frac{1}{m} \Delta W^{(l)} \right) + \lambda W^{(l)}\right] \\ b^{(l)} &= b^{(l)} - \alpha \left[\frac{1}{m} \Delta b^{(l)}\right] \end{align}

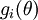即有 \textstyle g_i(\theta) 分别为：

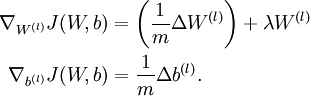
\begin{align} \nabla_{W^{(l)}} J(W,b) &= \left( \frac{1}{m} \Delta W^{(l)} \right) + \lambda W^{(l)} \\ \nabla_{b^{(l)}} J(W,b) &= \frac{1}{m} \Delta b^{(l)}. \end{align}

最后只需总体损失函数J(W，b)的偏导数与上述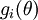\textstyle g_i(\theta) 的值比较即可。

除了梯度下降外，其他的常见的优化算法：1) 自适应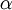\textstyle \alpha的步长，2) BFGS L-BFGS，3) SGD，4) 共轭梯度算法，以后涉及到再看。

posted @ 2016-03-20 10:20  ooon  阅读(440)  评论(0)  编辑  收藏  举报