(六) 6.2 Neurons Networks Backpropagation Algorithm
今天得主题是BP算法。大规模的神经网络可以使用batch gradient descent算法求解,也可以使用 stochastic gradient descent 算法,求解的关键问题在于求得每层中每个参数的偏导数,BP算法正是用来求解网络中参数的偏导数问题的。
先上一张吊炸天的图,可以看到BP的工作原理:
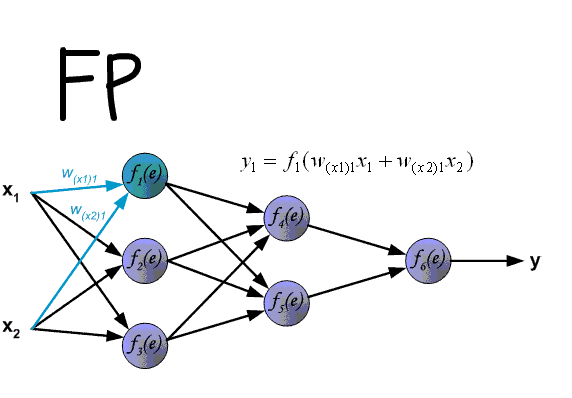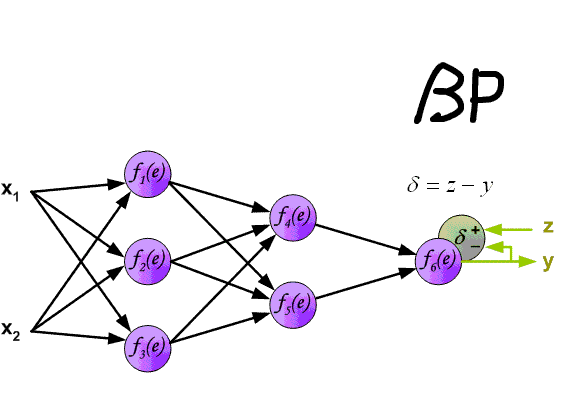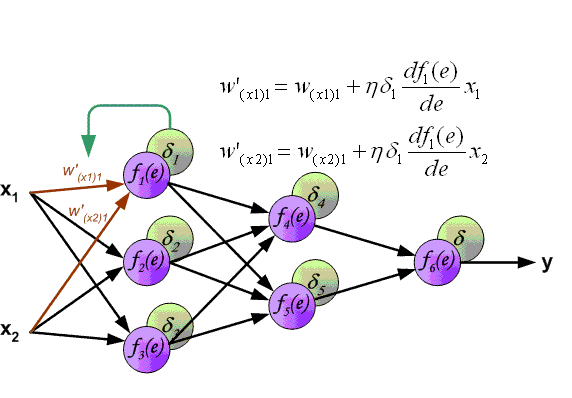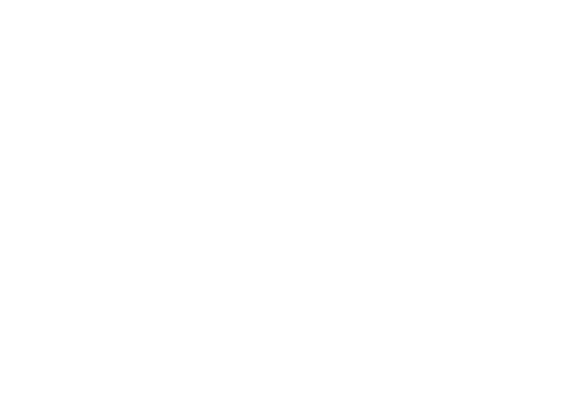
下面来看BP算法,用m个训练样本集合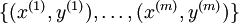 来train一个神经网络,对于该模型,首先需要定义一个代价函数,常见的代价函数有以下几种:
来train一个神经网络,对于该模型,首先需要定义一个代价函数,常见的代价函数有以下几种:
1)0-1损失函数:(0-1 loss function)

2)平方损失函数:(quadratic loss function)
3)绝对值损失函数:(absolute loss function)
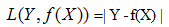
4)负log损失函数(log loss function)
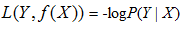
损失函数的意义在于,假设函数(hypothesis function,即模型)的输出与数据标签的值月接近,损失函数越小。反之损失函数越大,这样减小损失函数的值,来求得最优的参数即可,最后将最优的参数带入带假设函数中,即可求得最终的最优的模型。
在Neurons Network中,对于一个样本(x,y),其损失函数可表示为
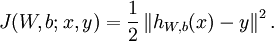
上式这种形式是平方损失函数(注意若采用交叉熵损失则与此损失形式不一样),对于所有的m个样本,对于所有训练数据,总的损失函数为:
![\begin{align}
J(W,b)
&= \left[ \frac{1}{m} \sum_{i=1}^m J(W,b;x^{(i)},y^{(i)}) \right]
+ \frac{\lambda}{2} \sum_{l=1}^{n_l-1} \; \sum_{i=1}^{s_l} \; \sum_{j=1}^{s_{l+1}} \left( W^{(l)}_{ji} \right)^2
\\
&= \left[ \frac{1}{m} \sum_{i=1}^m \left( \frac{1}{2} \left\| h_{W,b}(x^{(i)}) - y^{(i)} \right\|^2 \right) \right]
+ \frac{\lambda}{2} \sum_{l=1}^{n_l-1} \; \sum_{i=1}^{s_l} \; \sum_{j=1}^{s_{l+1}} \left( W^{(l)}_{ji} \right)^2
\end{align}](http://ufldl.stanford.edu/wiki/images/math/4/5/3/4539f5f00edca977011089b902670513.png)
上式中第一项为均方误差项,第二项为正则化项,用来限制权重W的大小,防止over-fitting,也即贝叶斯学派所说的给参数引入一个高斯先验的MAP(极大化后验)方法。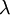 为正则项的参数,用来控制两项的相对重要性, 比如若
为正则项的参数,用来控制两项的相对重要性, 比如若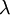 很大时,参数W,b必须很小才能使得最终的损失函数J(W,b) 很小。
很大时,参数W,b必须很小才能使得最终的损失函数J(W,b) 很小。
常见的分类或者回归问题,都可以用这个损失函数,注意分类时标签y是离散值,回归时对于sigmod函数y为(0,1)之间的连续值。对于tanh为(-1,1)之间的值。
BP算法的目标就是求得一组最优的W、b ,使得损失函数 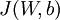 的值最小
的值最小
首先将每个参数 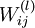 和
和 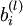 初始化为一个很小的随机值(比如说,使用正态分布
初始化为一个很小的随机值(比如说,使用正态分布 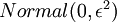 生成的随机值,其中
生成的随机值,其中 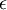 设置为
设置为 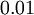 ),然后使用批梯度下降算法来优化
),然后使用批梯度下降算法来优化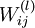 和
和 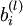 的值,因为
的值,因为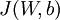 是非凸函数,即存在不止一个极值点,梯度下降算法很可能会收敛到局部极值处,但通常效果很不错(在浅层网络中,比如说三层),需要强调的是要将参数随机初始化,而不是全部置0,如果所有参数都用相同的值作为初始值,那么所有隐藏层单元最终会得到与输入值有关的、相同的函数(也就是说,对于所有hidden unit
是非凸函数,即存在不止一个极值点,梯度下降算法很可能会收敛到局部极值处,但通常效果很不错(在浅层网络中,比如说三层),需要强调的是要将参数随机初始化,而不是全部置0,如果所有参数都用相同的值作为初始值,那么所有隐藏层单元最终会得到与输入值有关的、相同的函数(也就是说,对于所有hidden unit  ,
,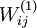 都会取相同的值,那么对于任何输入
都会取相同的值,那么对于任何输入  都会有:
都会有: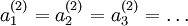 ),随机初始化会消除这种对称效果。
),随机初始化会消除这种对称效果。
批梯度下降算法中,每一次迭代都按照如下公式对参数 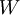 和
和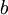 进行更新:
进行更新:
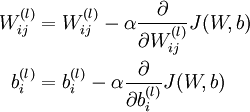
其中J(W,b)包含了所有的样本,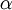 是学习速率,对于多层神经网络,如何计算每一层参数的偏导数是关键问题,BP算法正使用来计算每一项的偏导数的。
是学习速率,对于多层神经网络,如何计算每一层参数的偏导数是关键问题,BP算法正使用来计算每一项的偏导数的。
首先来看对于单个样例,参数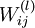 和
和 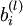 的偏导数分别为
的偏导数分别为 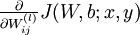 和
和 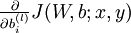
有了单个样例的偏导数后,根据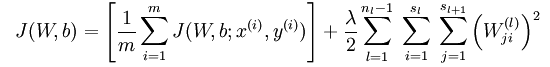 ,就可以很好求出损失函数
,就可以很好求出损失函数 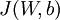 的偏导数:
的偏导数:
![\begin{align}
\frac{\partial}{\partial W_{ij}^{(l)}} J(W,b) &=
\left[ \frac{1}{m} \sum_{i=1}^m \frac{\partial}{\partial W_{ij}^{(l)}} J(W,b; x^{(i)}, y^{(i)}) \right] + \lambda W_{ij}^{(l)} \\
\frac{\partial}{\partial b_{i}^{(l)}} J(W,b) &=
\frac{1}{m}\sum_{i=1}^m \frac{\partial}{\partial b_{i}^{(l)}} J(W,b; x^{(i)}, y^{(i)})
\end{align}](http://ufldl.stanford.edu/wiki/images/math/9/3/3/93367cceb154c392aa7f3e0f5684a495.png)
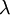 并不作用于bais unit b,所以第二个式子中没有第二项。
并不作用于bais unit b,所以第二个式子中没有第二项。
先看如下的式子,l+1层的输入等于l层的加权输出求和,即
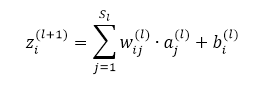
课件hidden layer的输入z为参数的方程,为了求解对每个样本中参数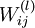 和
和 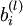 的偏导数,可以用根据链式求导法则有:
的偏导数,可以用根据链式求导法则有:
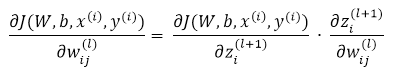

我们把上边的第一项称为残差,有了以上链式求导的思想,为了求得各个参数的偏导数,我们需要求得每一层的每个单元的残差。下面反向传播算法的思路:
1)给定 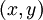 ,我们首先进行“前向传导”,计算出网络中所有的激活值,包括
,我们首先进行“前向传导”,计算出网络中所有的激活值,包括 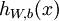 的输出值
的输出值
2)对第  层的每个节点
层的每个节点  ,计算出其“残差”
,计算出其“残差” 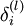 ,该残差表明节点对最终输出值的残差产生多少影响
,该残差表明节点对最终输出值的残差产生多少影响
3)对于最终的输出节点,直接算出网络产生的激活值与实际值之间的差距,将这个差距定义为 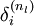
4)对于隐藏单元,将第  层节点的残差的加权平均值计算
层节点的残差的加权平均值计算  ,这些节点以
,这些节点以 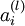 作为输入到
作为输入到  层
层
下面将给出反向传导算法的细节:
1)进行前馈传导计算,利用前向传导公式,得到 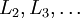 直到输出层
直到输出层 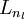 的激活值。
的激活值。
2)对于第 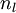 层(输出层)的每个输出单元
层(输出层)的每个输出单元  ,我们根据以下公式计算残差:
,我们根据以下公式计算残差:
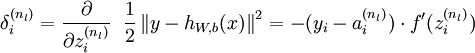
推倒:
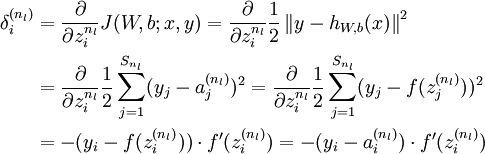
3)对 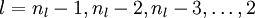 的各个层,第
的各个层,第  层的第
层的第  个节点的残差计算方法如下:
个节点的残差计算方法如下:
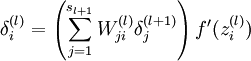
有了最后一层的层差,可以计算前一层的残差:
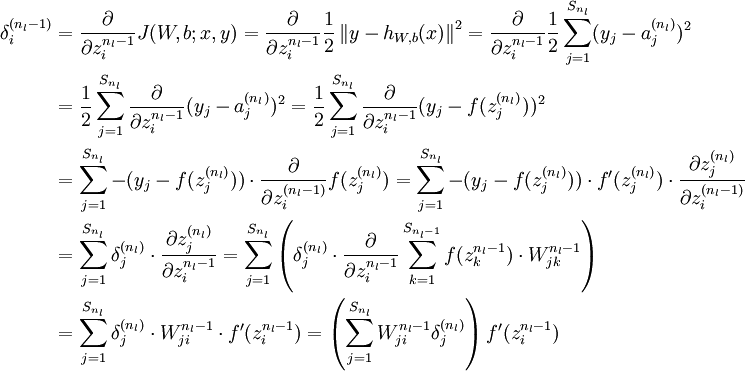
4)将上式中的  与
与 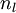 的关系替换为
的关系替换为  与
与  的关系,就可以得到:
的关系,就可以得到:
5)根据链式求导法则,计算方法如下:
![\begin{align}
\frac{\partial}{\partial W_{ij}^{(l)}} J(W,b; x, y) &= a^{(l)}_j \delta_i^{(l+1)} \\
\frac{\partial}{\partial b_{i}^{(l)}} J(W,b; x, y) &= \delta_i^{(l+1)}.
\end{align}]()
- 其中,第二项的计算公式如下:
- 根据
![]() ,有:
,有: ![]()
![]()
概括一下整个算法:
1)进行前馈传导计算,利用前向传导公式,得到 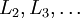 直到输出层
直到输出层 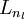 的激活值。
的激活值。
2)对输出层(第 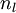 层),计算:
层),计算:
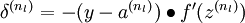
3)对于 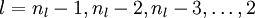 的各层,计算:
的各层,计算:
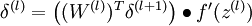
4)计算最终需要的偏导数值:
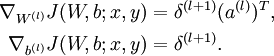
指的注意的是在以上的第2步和第3步中,我们需要为每一个 单元 值计算其
值计算其 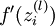 。假设
。假设 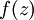 是sigmoid函数,f'(z)=f(z)*(1-f(z)),并且我们已经在前向传导运算中得到了
是sigmoid函数,f'(z)=f(z)*(1-f(z)),并且我们已经在前向传导运算中得到了 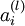 。那么,使用我们早先推导出的
。那么,使用我们早先推导出的 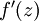 表达式,就可以计算得到
表达式,就可以计算得到 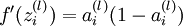 。
。
经过以上步骤,已经可以求出每个参数的偏导数,下一步就是更新参数,即使得参数沿梯度方向下降,下面给出梯度下降算法伪代码:
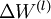 是一个与矩阵
是一个与矩阵 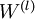 维度相同的矩阵,
维度相同的矩阵,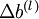 是一个与
是一个与 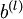 维度相同的向量。注意这里“
维度相同的向量。注意这里“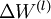 ”是一个矩阵,而不是“
”是一个矩阵,而不是“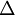 与
与 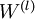 相乘”。下面,我们实现批量梯度下降法中的一次迭代:
相乘”。下面,我们实现批量梯度下降法中的一次迭代:
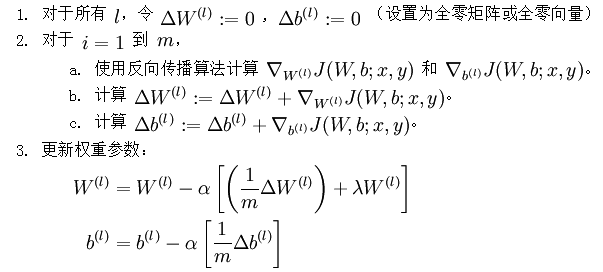
不断更新W,b的值,直到W,b不再变化为止,即网络达到收敛。
有机会再补上代码#24!!

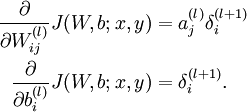
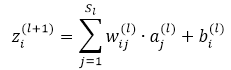 ,有:
,有: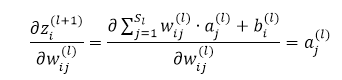


 浙公网安备 33010602011771号
浙公网安备 33010602011771号