D. Apple Tree Traversing
D. Apple Tree Traversing
There is an apple tree with $n$ nodes, initially with one apple at each node. You have a paper with you, initially with nothing written on it.
You are traversing on the apple tree, by doing the following action as long as there is at least one apple left:
- Choose an apple path $(u,v)$. A path $(u,v)$ is called an apple path if and only if for every node on the path $(u,v)$, there's an apple on it.
- Let $d$ be the number of apples on the path, write down three numbers $(d,u,v)$, in this order, on the paper.
- Then remove all the apples on the path $(u,v)$.
Here, the path $(u, v)$ refers to the sequence of vertices on the unique shortest walk from $u$ to $v$.
Let the number sequence on the paper be $a$. Your task is to find the lexicographically largest possible sequence $a$.
Input
Each test contains multiple test cases. The first line contains the number of test cases $t$ ($1 \le t \le 10^4$). The description of the test cases follows.
The first line of each test case contains a number $n$ ($1 \le n \le 1.5 \cdot 10^5$).
The following $n-1$ lines of each test case contain two numbers $u,v$ ($1 \le u,v \le n$). It's guaranteed that the input forms a tree.
It is guaranteed that the sum of $n$ over all test cases does not exceed $1.5 \cdot 10^5$.
Output
For each test case, output the lexicographically largest sequence possible $a_1, a_2, \ldots, a_{|a|}$. It can be shown that $|a| \le 3 \cdot n$.
Example
Input
6
4
1 2
1 3
1 4
4
2 1
2 4
2 3
5
1 2
2 3
3 4
4 5
1
8
6 3
3 5
5 4
4 2
5 1
1 8
3 7
6
3 2
2 6
2 5
5 4
4 1Output
3 4 3 1 2 2
3 4 3 1 1 1
5 5 1
1 1 1
5 8 7 2 4 2 1 6 6
5 6 1 1 3 3 Note
In the first test case, we do the following steps:
- Choose the apple path $(4, 3)$. This path consists of the nodes $4, 1, 3$, and each of them have an apple (so it is a valid apple path). $d = 3$ as there are $3$ apples on this path. Append $3, 4, 3$ in that order to our sequence $a$. Now, remove the apples from these $3$ vertices.
- Only node $2$ has an apple left. Choose the apple path $(2, 2)$. This path only consists of the single node $2$. $d = 1$ as there is $1$ apple on this path. Append $1, 2, 2$ in that order to our sequence $a$ and remove the apple from $2$.
The final sequence is thus $[3, 4, 3, 1, 2, 2]$. It can be shown this is the lexicographically largest sequence possible.
解题思路
直接暴力找直径然后递归处理挂在直径上的子树,只要敢交就过了。实际上这题的难点在于证明这个做法的复杂度。
首先解释一下为什么要找直径。对于初始的 $n$ 个节点的树,假设其直径长度为 $d$(直径上的节点个数),对应的两个字典序最大的端点分别为 $u$ 和 $v$($u > v$)。如果我们随便找一条长度小于 $d$ 的路径 $(d',u',v') < (d,u,v)$,显然不如直径的字典序大。而对于初始树的直径对应的 $(d,u,v)$ 是所有可能的三元组中字典序最大的(后面会证明挂在这条直径的子树的直径严格小于 $d$),因此我们必然选择该直径。
把这条直径拉直,就会发现初始的树变成一条链上挂着若干个子树的形式,如下图(直径由颜色标出):
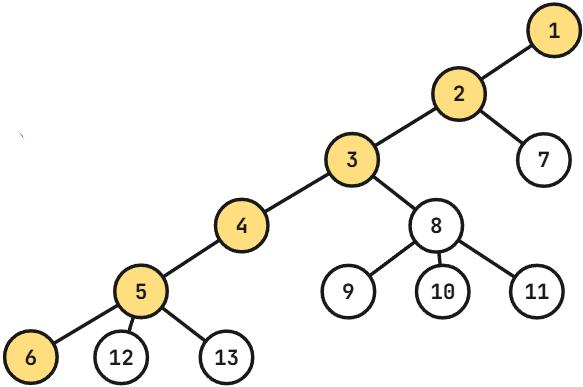
当删除这条直径后,这些子树就会相互独立,形成森林。可以用归纳法证明,对于森林中的每棵树应该优先选择两个字典序最大端点的直径。
先不考虑复杂度的问题,想到上述贪心的思路后就可以暴力地递归解决了。
- 定义森林 $S$ 里面有若干棵独立的树。我们用每棵树的根节点 $r_i$ 来表示这棵树,因此有 $r_i \in S$。初始时 $S := \{1\}$(取决于选择哪个节点作为初始树的根)。
- 依次枚举 $S$ 中的每棵树。对于每棵树,先通过两遍 dfs 找到树的直径(包括直径长度、两个字典序最大的直径端点以及整条直径上的节点)。再标记直径上的每个节点(表示删除该节点)。最后再次枚举直径上的每个节点,对于每个节点枚举其邻接点,如果邻接点 $v$ 没被标记过则说明找到挂在直径上的某棵子树,直接用 $v$ 表示该子树的根,并加入到集合 $T$ 中。
- 令 $S:=T$,如果 $S$ 不为空则重复步骤 $2$。
实际上上述做法的时间复杂度为 $O(n \sqrt{n})$,下面来证明。
如上图所示当删除直径后,会得到若干棵独立的树,容易知道每棵树的直径不超过 $d$。那是否会存在直径也等于 $d$ 的树呢?答案是不存在的,每棵树的直径实际上严格小于 $d$。证明参考下面折叠的内容。
证明
性质:对于一棵树中的两条直径,至少经过一个公共节点。
证明:反证法,设两条没有公共节点的直径分别为 $a_1, a_2, \ldots a_d$ 和 $b_1, b_2, \ldots b_d$。考虑这两条直径中最近的两个点,假设为 $a_i$ 和 $b_j$,由前面假设知道路径 $(a_i, b_j)$ 不经过两条直径的其余节点。定义 $dist(a_i, b_j)$ 表示路径 $(a_i, b_j)$ 的长度(路径上的节点数量),容易知道 $dist(a_i, b_j) \geq 2$。考虑以下四种情况:
- $i \geq \frac{d+1}{2},\, j \geq \frac{d+1}{2}$。$dist(a_1,b_1) = i-1 + dist(a_i, b_j) + j-1 \geq d+1$,与直径长度为 $d$ 矛盾。
- $i \geq \frac{d+1}{2},\, j < \frac{d+1}{2}$。$dist(a_1, b_d) = i-1 + dist(a_i, b_j) + d-j \geq d+1$,与直径长度为 $d$ 矛盾。
- $i < \frac{d+1}{2},\, j \geq \frac{d+1}{2}$。$dist(a_d, b_1) = d-i + dist(a_i, b_j) + j-1 \geq d+1$,与直径长度为 $d$ 矛盾。
- $i < \frac{d+1}{2},\, j < \frac{d+1}{2}$。$dist(a_d, b_d) = d-i + dist(a_i, b_j) + d-j \geq d+1$,与直径长度为 $d$ 矛盾。
因此一棵树中的任意两条直径至少经过一个公共节点。
在该性质的基础上,对于一棵删除直径后得到的子树,如果其直径长度为 $d$,说明与被删除的直径有至少一个公共节点。但公共节点只可能是被删除直径上的节点,而现在直径被删除,意味着不可能有公共节点,因此矛盾。所以子树的直径严格小于 $d$。
这意味着在每一轮的步骤 $2$ 中,找到的最大直径是严格单调递减的,进而得出步骤 $2$ 至多执行 $O(\sqrt{n})$ 轮。这是一个经典问题,有 $d_1 + d_2 + \cdots + d_m \leq n$,其中 $d_i > 0$ 且 $d_{i} < d_{i+1}$,问 $m$ 最大能取多少。显然我们应该贪心地依次取 $1, 2, \ldots m$,有 $\frac{m(1+m)}{2} \leq n \Rightarrow m \leq \sqrt{2n}$。我们把每个 $d_i$ 看作是第 $i$ 轮的步骤 $2$ 找到的最大直径长度,因此可以发现步骤 $2$ 最多执行 $O(\sqrt{n})$ 轮,而每轮我们都要遍历集合 $S$ 中的每棵树,总的复杂度可以粗略看作 $O(n)$,因此上述做法的时间复杂度为 $O(n \sqrt{n})$。
AC 代码如下,时间复杂度为 $O(n\sqrt{n})$:
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 1.5e5 + 5, M = N * 2;
int h[N], e[M], ne[M], idx;
int d[N], f[N];
bool vis[N];
vector<int> g;
void add(int u, int v) {
e[idx] = v, ne[idx] = h[u], h[u] = idx++;
}
void dfs(int u, int p) {
d[u] = d[p] + 1;
f[u] = p;
g.push_back(u);
for (int i = h[u]; i != -1; i = ne[i]) {
int v = e[i];
if (v == p || vis[v]) continue;
dfs(v, u);
}
}
void solve() {
int n;
cin >> n;
idx = 0;
memset(h, -1, n + 1 << 2);
for (int i = 0; i < n - 1; i++) {
int u, v;
cin >> u >> v;
add(u, v), add(v, u);
}
vector<array<int, 3>> ans;
queue<int> q({1});
memset(vis, 0, n + 1);
while (!q.empty()) {
int u = q.front();
q.pop();
g.clear();
dfs(u, 0);
auto cmp = [&](int i, int j) {
if (d[i] != d[j]) return d[i] < d[j];
return i < j;
};
int x = *max_element(g.begin(), g.end(), cmp);
g.clear();
dfs(x, 0);
int y = *max_element(g.begin(), g.end(), cmp);
ans.push_back({d[y], max(x, y), min(x, y)});
for (int i = y; i; i = f[i]) {
vis[i] = true;
}
for (int i = y; i; i = f[i]) {
for (int j = h[i]; j != -1; j = ne[j]) {
int v = e[j];
if (!vis[v]) q.push(v);
}
}
}
sort(ans.begin(), ans.end(), greater<array<int, 3>>());
for (auto &[d, x, y] : ans) {
cout << d << ' ' << x << ' ' << y << ' ';
}
cout << '\n';
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int t;
cin >> t;
while (t--) {
solve();
}
return 0;
}
参考资料
Codeforces Round 1023 (Div 2) Editorial:https://codeforces.com/blog/entry/142642
本文来自博客园,作者:onlyblues,转载请注明原文链接:https://www.cnblogs.com/onlyblues/p/18868469



 浙公网安备 33010602011771号
浙公网安备 33010602011771号