Path Existence Queries in a Graph II

Path Existence Queries in a Graph II

You are given an integer n representing the number of nodes in a graph, labeled from 0 to n - 1.

You are also given an integer array nums of length n and an integer maxDiff.

An undirected edge exists between nodes i and j if the absolute difference between nums[i] and nums[j] is at most maxDiff (i.e., |nums[i] - nums[j]| <= maxDiff).

You are also given a 2D integer array queries. For each queries[i] = [ui, vi], find the minimum distance between nodes ui and v_i. If no path exists between the two nodes, return -1 for that query.

Return an array answer, where answer[i] is the result of the ith query.

Note: The edges between the nodes are unweighted.

 

Example 1:

Input: n = 5, nums = [1,8,3,4,2], maxDiff = 3, queries = [[0,3],[2,4]]

Output: [1,1]

Explanation:

The resulting graph is:

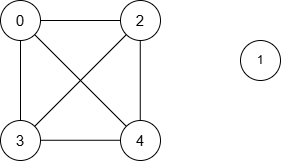
Query	Shortest Path	Minimum Distance
[0, 3]	0 → 3	1
[2, 4]	2 → 4	1

Thus, the output is [1, 1].

Example 2:

Input: n = 5, nums = [5,3,1,9,10], maxDiff = 2, queries = [[0,1],[0,2],[2,3],[4,3]]

Output: [1,2,-1,1]

Explanation:

The resulting graph is:

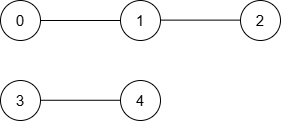
Query	Shortest Path	Minimum Distance
[0, 1]	0 → 1	1
[0, 2]	0 → 1 → 2	2
[2, 3]	None	-1
[4, 3]	3 → 4	1

Thus, the output is [1, 2, -1, 1].

Example 3:

Input: n = 3, nums = [3,6,1], maxDiff = 1, queries = [[0,0],[0,1],[1,2]]

Output: [0,-1,-1]

Explanation:

There are no edges between any two nodes because:

• Nodes 0 and 1: |nums[0] - nums[1]| = |3 - 6| = 3 > 1
• Nodes 0 and 2: |nums[0] - nums[2]| = |3 - 1| = 2 > 1
• Nodes 1 and 2: |nums[1] - nums[2]| = |6 - 1| = 5 > 1

Thus, no node can reach any other node, and the output is [0, -1, -1].

 

Constraints:

• 1 <= n == nums.length <= 105
• 0 <= nums[i] <= 105
• 0 <= maxDiff <= 105
• 1 <= queries.length <= 105
• queries[i] == [ui, vi]
• 0 <= ui, vi < n

 

解题思路

  这场早上去看医生没打，补一下题。

  假设 nums 数组是非递减排序的（可以通过值绑定下标排序得到），那么对于每个点 $i$，其可以向前面某段连续区间的点 $(k \in [j, i-1] \, (1 \leq j < i, )$ nums[i] - nums[k] < maxDiff$)$ 连边。对于询问 $(a,b)$，不失一般性假设 $a \geq b$，考虑从 $a$ 往左到达 $b$ 的最短距离。显然 $a$ 应该往编号小的点走，假设 $a$ 与前面区间 $[j, a-1]$ 内的点连边。如果 $ j \leq b < a$，直接从 $a$ 走到 $b$ 即可。否则 $a$ 应该尽可能往左走到 $j$。假设在最优解中这一步选择的是 $k \in [j+1,a-1]$，然后从 $k$ 又往前走到某个点 $u$，而 $j$ 也可以走到 $u$，这是因为 nums[k] - nums[u] <= nums[j] - nums[u] <= maxDiff。因此可以通过调整将 $k$ 换成 $j$，最优解仍成立。这是本题最关键的地方。

  因此对于每个点，我们可以先通过双指针找到其往左最远能直接到达到的点。然后对于每个询问 $(a,b)$，我们可以从 $a$ 开始不断的往最左边能到达的点跳，但这个过程容易被卡到 $O(n)$ 的复杂度。此时我们可以考虑倍增，即维护从每个点 $i$ 开始往左跳 $2^j$ 步能到达的点，定义为 $fa[i][j]$。从 $j= \left\lfloor\log{n}\right\rfloor$ 开始往小枚举到 $0$，如果 $fa[a][j] > b$，意味着从 $a$ 跳到 $fa[a][i]$ 还没到达 $b$，此时则往左跳 $2^j$ 步，有 $a \gets fa[a][i]$（原理类似 lca）。最后再判断往左跳 $1$ 步能否恰好达到 $b$，不能的话说明无解。

  AC 代码如下，时间复杂度为 $O(n \log{n})$：

class Solution {
public:
    vector<int> pathExistenceQueries(int n, vector<int>& nums, int maxDiff, vector<vector<int>>& queries) {
        vector<int> p(n);
        iota(p.begin(), p.end(), 0);
        sort(p.begin(), p.end(), [&](int i, int j) {
            return nums[i] < nums[j];
        });
        vector<vector<int>> fa(n, vector<int>(17));
        for (int i = 0, j = 0; i < n; i++) {
            while (nums[p[i]] - nums[p[j]] > maxDiff) {
                j++;
            }
            fa[i][0] = j;
            for (int j = 1; j <= 16; j++) {
                fa[i][j] = fa[fa[i][j - 1]][j - 1];
            }
        }
        vector<int> mp(n);
        for (int i = 0; i < n; i++) {
            mp[p[i]] = i;
        }
        vector<int> ans;
        for (auto &q : queries) {
            int a = mp[q[0]], b = mp[q[1]];
            if (a < b) swap(a, b);
            int s = 0;
            for (int i = 16; i >= 0; i--) {
                if (fa[a][i] > b) {
                    a = fa[a][i];
                    s |= 1 << i;
                }
            }
            if (fa[a][0] > b) s = -1;
            else if (a != b) s++;
            ans.push_back(s);
        }
        return ans;
    }
};

 

参考资料

  3534. 针对图的路径存在性查询 II - 力扣（LeetCode）：https://leetcode.cn/problems/path-existence-queries-in-a-graph-ii/solutions/3663255/tan-xin-bei-zeng-by-tsreaper-vygl/