G. Game With Triangles: Season 2

G. Game With Triangles: Season 2

There is a regular polygon with $n$ sides ($n \ge 3$). The vertices are indexed as $1,2,\ldots,n$ in clockwise order. On each vertex $i$, the pink soldiers have written a positive integer $a_i$. With this regular polygon, you will play a game defined as follows.

Initially, your score is $0$. Then, you perform the following operation any number of times to increase your score.

• Select $3$ different vertices $i$, $j$, $k$ that you have not chosen before, and draw the triangle formed by the three vertices.
  • Then, your score increases by $a_i \cdot a_j \cdot a_k$.
  • However, you can not perform this operation if the triangle shares a positive common area with any of the triangles drawn previously.

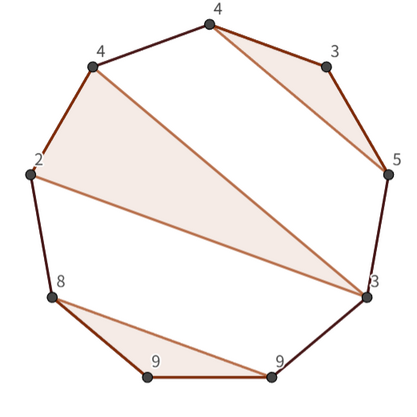
An example of a state after two operations is on the left. The state on the right is impossible as the two triangles share a positive common area.

Your objective is to maximize the score. Please find the maximum score you can get from this game.

Input

Each test contains multiple test cases. The first line contains the number of test cases $t$ ($1 \le t \le 10^4$). The description of the test cases follows.

The first line of each test case contains a single integer $n$ — the number of vertices ($3 \le n \le 400$).

The second line of each test case contains $a_1,a_2,\ldots,a_n$ — the integers written on vertices ($1 \le a_i \le 1000$).

It is guaranteed that the sum of $n^3$ over all test cases does not exceed $400^3$.

Output

For each test case, output the maximum score you can get on a separate line.

Example

Input

6
3
1 2 3
4
2 1 3 4
6
2 1 2 1 1 1
6
1 2 1 3 1 5
9
9 9 8 2 4 4 3 5 3
9
9 9 3 2 4 4 8 5 3

Output

6
24
5
30
732
696

Note

On the first test case, you can draw only one triangle. The maximum score $6$ is found by drawing the triangle with $i=1$, $j=2$, $k=3$.

On the second test case, you can draw only one triangle. The maximum score $24$ is found by drawing the triangle with $i=1$, $j=3$, $k=4$.

On the third test case, you can draw two triangles. There is a series of two operations that leads to the score $5$, which is the maximum.

On the fourth test case, you can draw two triangles. However, drawing two triangles leads to a score of either $6+5=11$, $15+2=17$, or $10+3=13$. The maximum score $30$ is found by drawing only one triangle with $i=2$, $j=4$, $k=6$.

On the fifth test case, you can draw three triangles. The maximum score $732$ is found by drawing three triangles as follows.

 

解题思路

  做法是区间 dp。怎么想到的呢？假设有一个 $n$ 个顶点的多边形，我们随机选择 $3$ 个不同的顶点 $x,y,z \, (x < y < z)$ 来构成三角形，由于之后选择的三角形不能与当前三角形有任何交集，因此由三条边 $xy$，$yz$，$zx$ 划分出来的三个部分节点，每个部分的节点只能在其各自内部选择。即 $x+1$ 到 $y-1$ 的节点只能在 $x+1$ 到 $y-1$ 中选择，同理 $y+1$ 到 $z-1$ 的节点，$z+1$ 到 $x-1$ 的节点（编号超过 $n$ 的节点从 $1$ 开始重新计数）。我们可以将每部分的节点重新看作相应的多边形来求解，这相当于是一个更小的子问题，因此考虑用 dp。

  定义状态 $f(l,r)$ 表示由顶点 $l$ 到 $r$ 顺时针构成的多边形中，所有合法划分方案（即不同顶点构成没有交集的三角形）的最大值。实际上困难的地方在于状态转移，不好想或漏掉某些情况。

  我们可以将所有的合法划分方案根据是否选择顶点 $l$，$r$ 分成以下 $4$ 类：

• 选择 $l$ 不选择 $r$，此时直觉上容易看作状态 $f(l,r-1)$。实际上这并不完全正确，根据定义 $f(l,r-1)$ 对应由顶点 $l$ 到 $r-1$ 顺时针构成的多边形的方案，确实不包含顶点 $r$，但顶点 $l$ 可以选或不选。应该说 $f(l,r-1)$ 包含了选择 $l$ 不选择 $r$ 的情况，由于也包含了不选择 $l$ 不选择 $r$ 的情况，因此不能说就等于 $f(l,r-1)$ 这个状态。由于不选择 $l$ 不选择 $r$ 的情况也属于 $f(l,r)$ 表示的状态，每个状态求的是最大值，因此有重复方案并不影响结果的正确性。
• 不选择 $l$ 选择 $r$，可以用状态 $f(l+1,r)$ 来表示（正确的分析同上）。
• 不选择 $l$ 不选择 $r$，可以用状态 $f(l+1,r-1)$ 来表示。实际上状态 $f(l,r-1)$ 和 $f(l+1,r)$ 都包含了状态 $f(l+1,r-1)$，因此可以不选（在代码中就没有考虑）。
• 选择 $l$ 选择 $r$。此时又分成两种情况：
  • $l$ 和 $r$ 是同一个三角形的顶点，此时我们可以枚举另外一个顶点 $k \, (l < k < r)$，那么能取得的最大值就是 $\max\limits_{l<k<r}\{ f(l,k-1) + f(k+1,r) + a_l \cdot a_k \cdot a_r \}$。
  • $l$ 和 $r$ 不是同一个三角形的顶点，意味着 $l$ 和 $r$ 分别属于两个不同的三角形，那么我们考虑分界点 $k \, (l \leq k < r)$ 把多边形分成两个部分，能取得的最大值就是 $\max\limits_{l \leq k<r}\{ f(l,k) + f(k+1,r)\}$。

  因此状态转移方程就是

$$f(l,r) = \max\left\{ f(l,r-1), \, f(l+1, r), \, f(l+1,r-1), \, \max\limits_{l<k<r}\{ f(l,k-1) + f(k+1,r) + a_l \cdot a_k \cdot a_r \}, \, \max\limits_{l \leq k<r}\{ f(l,k) + f(k+1,r) \} \right\}$$

  最后答案就是 $\max\limits_{1 \leq i < n}\{f(i,i+n-1)\}$。

  AC 代码如下，时间复杂度为 $O\left(n^3\right)$：

#include <bits/stdc++.h>
using namespace std;

typedef long long LL;

const int N = 805;

int a[N];
LL f[N][N];

void solve() {
    int n;
    cin >> n;
    for (int i = 0; i < n; i++) {
        cin >> a[i];
        a[i + n] = a[i];
    }
    for (int len = 3; len <= n; len++) {
        for (int i = 0; i + len - 1 < n << 1; i++) {
            int j = i + len - 1;
            f[i][j] = max(f[i + 1][j], f[i][j - 1]);
            for (int k = i + 1; k < j; k++) {
                f[i][j] = max(f[i][j], f[i + 1][k - 1] + f[k + 1][j - 1] + 1ll * a[i] * a[k] * a[j]);
                f[i][j] = max(f[i][j], f[i][k] + f[k + 1][j]);
            }
        }
    }
    LL ret = 0;
    for (int i = 0; i < n; i++) {
        ret = max(ret, f[i][i + n - 1]);
    }
    cout << ret << '\n';
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int t;
    cin >> t;
    while (t--) {
        solve();
    }
    
    return 0;
}

 

参考资料

  Codeforces Round 1009 (Div. 3) — Editorial：https://codeforces.com/blog/entry/140540

  Codeforces Round 1009 (Div. 3)：https://www.cnblogs.com/maburb/p/18766581