【专题】计数问题（排列组合，容斥原理，Prufer序列）

【容斥原理】

对于统计指定排列方案数的问题，一个方案是空间中的一个元素。

定义集合x是满足排列中第x个数的限定条件的方案集合，设排列长度为S，则一共S个集合。

容斥原理的本质是考虑[集合交 或 集合交的补集]和[集合并 或 集合并的补集]之间相互转化的问题。

定义目标函数为f(m)，已知函数g(T)。（例如已知集合并，则T表示所有T个集合的集合并，通常g(T)=C(n,T)*T个集合的集合并）

当两者都不是补集或两者都是补集时，有f(S)=Σ(-1)^|T|-1g(T)，其中T为S的非空子集，即奇加偶减。

当两者中有且仅有一者是补集时，有f(S)=Σ(-1)^|T|g(T)，其中T为S的子集，要把空集的补集（即全集）算入。

要特别注意补集的情况下，g(T)表示T的补集，记住无论如何原集从小到大。

例如已知集合并，求解集合交，容斥原理就是将所有集合组合方案的集合并乘以由集合个数决定的容斥系数，得到S个集合的集合交。

莫比乌斯函数μ相关的容斥：对于统计指定数字数量的问题，一个数字是空间中的一个元素，定义集合x（x是素数）是含有素因子x的数字集合。

那么枚举所有数字就是枚举集合交，μ就是(-1)^k（k是素因子个数）即容斥系数。

最后，当限制条件取反时，交集变成并集的补集，并集变成交集的补集。

★自带容斥：可以省略系数的计算，对每个数计算【集合减去内部所有包含的交集】，然后求和即可。

具体见：【CodeForces】585 E. Present for Vitalik the Philatelist

【SRM20】数学场 T2

看到计数想容斥。

 

例题：

1.对一个n*m的棋盘染色，每格可以是黑色或白色，要求每行每列都有黑格。

定义一个集合为指定行列含有黑格，则题目要求集合交。

只有集合并的补集可以计算，即一些行一些列全是白格（是一些行一些列有黑格的补集），枚举行列，则选出i行j列的方案数是C(n,i)C(m,j)，这i行j列全是白格的方案数是2^(n-i)(m-j)。

所以答案就是Σ(-1)^i+jC(n,i)C(m,j)2^(n-i)(m-j)，0<=i<n，0<=j<m。

2.对一个n*m的棋盘染色，每格可以是黑色或白色，要求存在一行或一列全是黑格。

定义一个集合为指定行列含有白格，则题目要求集合交的补集，仍然用集合并的补集求解。

ans=Σ(-1)^i+j-1C(n,i)C(m,j)2^(n-i)(m-j)（状态(0,1)和(1,0)）。

3.对一个n*m的棋盘染色，每格可以是黑色或白色，要求存在一行和一列全是黑格。

定义一个集合为指定行列含白格，则题目要求两个集合交的补集。

需要满足的条件是：（A）存在一行都是黑格。（B）存在一列都是黑格。

先对A用容斥原理，答案为Σ(-1)^i-1C(n,i)*(有i行都是黑格且满足B的方案数)。（暂将B作为全局约束）

再对B用容斥原理，答案为Σ(-1)^i-1C(n,i)*Σ(-1)^j-1C(m,j)*(有i行j列都是黑格的方案数)。

化简一下就是Σ(-1)^i+jC(n,i)C(m,j)2^(n-i)(m-j)，其中i,j>=1。

4.倍数相关的容斥，莫比乌斯函数μ可以作为系数。

5.错排问题：一种排列错排为1，不错排为0，求解集合交，已知集合并的补集，即ans=Σ(-1)^i*C(n,i)*(n-i)!。

 

【排列组合】

<加法原理>做一件事情有n个方法，第i个方法有pi种方案，则一共有p1+p2+...+pn种方案。

<乘法原理>做一件事件有n个步骤，第i个步骤有pi种方案，则一共有p1p2...pn种方案。

乘法原理是加法原理的特殊情况，加法原理的关键是不重不漏地分类，若有重复可以考虑容斥原理。

<排列>A(n,m)表示在n个数中选m个的排列数（n为下标，m为上标）

由乘法原理，每个步骤选择一个数，则分别有n,n-1,...n-m+1种选择，则可以简单地表示为：

A(n,m)=n*(n-1)*...*(n-m+1)即

A(n,m)=n!/(n-m)!

特别地，n个数的全排列是A(n,n)=n!

<组合>C(n,m)表示在n个数中选m个的组合数（n为下标，m为上标）

首先选出m个数的组合，然后把这m个数进行全排列。由乘法原理知A(n,m)=C(n,m)*A(m,m)，即C(n,m)=A(n,m)/A(m,m)=n!/((n-m)!m!)。

C(n,m)=n!/((n-m)!m!)

<组合数性质>

1.C(n,0)=C(n,n)=1

2.核心性质一：C(n,k)=C(n,n-k)　　组合的对称性！

3.核心性质二：C(n+1,k+1)=C(n,k)+C(n,k+1)　　组合数的递推公式（杨辉三角）。

证明：n+1个数里面选择k+1个数有两类方法，若选择第一个数则转化为C(n,k)，否则转化为C(n,k+1)。

4.C(n,k+1)=C(n,k)*(n-k)/(k+1)　　组合数同下标递推公式

　　直接利用公式变换：

　　　　C(n,k+1)=n(n-1)...(n-k+1)(n-k)/(k+1)!

　　　　C(n,k)=n(n-1)...(n-k+1)/k!

　　两式相除得C(n,k+1)/C(n,k)=(n-k)/(k+1)

此性质可用于二项式定理(后面介绍)的预处理过程。

★性质：ΣC(n,0~n)=2^n。

5.重复元素问题：排列组合往往不是简单的C和A公式一写就可以解决的，因为有大量的重复元素，需要做大量去重工作。

　　(1)有重复元素的全排列。

　　　　有k个元素，其中第i个元素有n_i个，求全排列个数。

　　　　令总数为n，设答案为x。对于答案中的每个排列，对相同元素标号后，相同元素内部可以再进行全排列，所以：

　　　　n₁!n₂!n₃!...n_k!x=n!得到x=n!/(n₁!n₂!n₃!...n_k!)

　　　　这里和组合数的推导一样，从而得到结论：加上m个数的标号就是乘m个数的全排列，去除m个数的标号就是除以m个数的全排列。

　　(2)★可重复选择的组合。

　　　　问题：n个数中取k个，每个数可以取多次，求组合。

　　　　　试着反过来考虑，把k个1划分成n段的方案数。

　　　　　问题转化为求解x1+x2+...+xn=k的非负整数解个数，由于0很麻烦，所以令xi=xi+1，则转化为：

　　　　　求解x1+x2+...+xn=k+n的正整数解的个数。

　　　　　想象有k+n个“1”排成一排，则问题等价于把这些“1”分成n个部分的方法数。

　　　　　隔板法：重复问题中常转化为x1+x2...+xn=X的形式，然后可以想象为在X-1个间隔中放置n-1个隔板。当隔出区间可能为0时，整体+1。

　　　　　那么在k+n-1个间隔中选n-1个，即ans=C(k+n-1,n-1)=C(n+k-1,k)。

6.正难则反的思想（补集思想），在这类数学问题中尤其常用，而且往往十分隐蔽、不易发现。

#include<cstdio>
#include<cstring>
#include<cctype>
#include<cmath>
#include<algorithm>
#define ll long long
using namespace std;
int read(){
    char c;int s=0,t=1;
    while(!isdigit(c=getchar()))if(c=='-')t=-1;
    do{s=s*10+c-'0';}while(isdigit(c=getchar()));
    return s*t;
}
int min(int a,int b){return a<b?a:b;}
int max(int a,int b){return a<b?b:a;}
int abs(int x){return x>0?x:-x;}
void mins(int &a,int b){if(a>b)a=b;}
void maxs(int &a,int b){if(a<b)a=b;}
//void insert(int u,int v){tot++;e[tot].v=v;e[tot].from=first[u];first[u]=tot;}
/*------------------------------------------------------------*/
const int inf=0x3f3f3f3f,MOD=1000000007;
ll n;

void gcd(ll a,ll b,ll& d,ll& x,ll& y){
    if(!b){d=a;x=1;y=0;}
     else{gcd(b,a%b,d,y,x);y-=x*(a/b);}
}
ll inv(ll a,ll n){
    ll d,x,y;
    gcd(a,n,d,x,y);
    return (x%n+n)%n;
}
ll fac[1010],fav[1010];
ll C(ll n,ll m){return fac[n]*fav[m]%MOD*fav[n-m]%MOD;}
int main(){
    fac[0]=1;fav[0]=1;
    for(int i=1;i<=1001;i++)fac[i]=fac[i-1]*i%MOD;
    for(int i=1;i<=1001;i++)fav[i]=inv(fac[i],MOD);
    
    return 0;
}

 

例题：

1.n个数字的和不超过m的的方案数。

若是等于m，则求C(n+m-1,n-1)即(n+m-1,m)。

转化为求ΣC(n+i-1,i)，由组合数递推公式C(n,m)=C(n-1,m-1)+C(n-1,m)得

C(n-1,0)+C(n,1)+C(n+1,2)+C(n+2,3)+...+C(n+m-1,m)

=C(n,0)+C(n,1)+C(n+1,2)+C(n+2,3)+...+C(n+m-1,m)

=C(n+m,m)　　两两一步一步凑剩一个数字。

2.袋球模型

①n个不同的球和m个不同的袋子

每个球都有m中选择，ans=m^n。

②n个相同的球和m个不同的袋子

视为将n+m个'1'分成m段，所以ans=C(n+m-1,m-1)。

③n个不同的球和m个相同的袋子——将1~n划分成m份的方案数

设f[i][j]表示将1~i划分成j份（每份不为0）的方案数，考虑数字 i 可以新开一个袋子，或放到之前的袋子。（强制不为0是因为从0变成1时不会重复）

所以f[i][j]=f[i-1][j-1]+f[i-1][j]*j。然后再统计Σf[n][i]。

④n个相同的球和m个相同的袋子——将n划分成m个非负整数的方案数

设f[i][j]表示将 i 划分成 j 个非负整数的方案数，如果方案有0则依赖于f[i][j-1]，否则整体-1依赖于f[i-j][j]。

所以f[i][j] = f[i][j-1] + f[i-j][j] 。

 

<二项式定理>

观察杨辉三角可以发现，它的第i行的数字是C(i-1,0),C(i-1,1)...C(i-1,i-1)，即同一行同下标，上标从0开始递增。

由杨辉三角也可以发现组合数的两大核心性质（同行左右对称，每个数等于上面和上面左边两数之和）。

另一方面，把(a+b)^n展开的多项式系数和杨辉三角一致，由此可得

★二项式定理：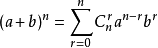

其中组合数对应杨辉三角也对应系数，后边对应项的内容。

也可以理解为n个括号，多少个选a，多少个选b出来的结果。

而求解系数可以使用组合数性质4。

 

【卡特兰数】算法专题：卡特兰数（计数数列）——onion_cyc

 

【集合划分数】【算法专题】集合划分数（斯特林数与贝尔数）

【Prufer序列】带标号无根树计数

参考：树的计数 + prufer序列与Cayley公式 学习笔记

Matrix67: The Aha Moments

一、构造Prufer序列：对于一棵带标号无根树，定义度为1的节点为“叶子节点”，每次找到编号最小的叶子节点删除，并将其邻点加入Prufer序列，重复直至剩余两个点为止（故Prufer序列的长度为n-2）。

构造过程用堆维护叶子节点即可，复杂度O(n log n)。

二、还原无根树：对于点集{1,2,...,n}，每次选择最小的不在Prufer序列中的编号x，以及Prufer序列的第一个数字y（最早加入的），将x和y连边，然后从点集种删除x，从Prufer序列中删除y。重复以上过程直至Prufer序为空，此时将点集中剩余的两个编号连边即可。

证明：还原的思路是通过Prufer序列依次找到原来的删除点。最开始的时候，在Prufer序列中的点说明度不为1（邻点删除会将其加入Prufer序），所以不在Prufer序中的编号最小的节点就是最先删除的“编号最小的叶子节点”，将这个点和Prufer序的第一个数连边（其邻点）连边。然后从点集中删除就是该点已经不能再删，从Prufer序中删除就是将度-1。

这也很容易看出，点x在Prufer序中的出现次数=点x的度-1。

还原过程先将不在Prufer序中的节点加入堆，过程中维护这个堆即可，复杂度O(n log n)。

三、推广：

① Cayley公式：由于由数字1~n构成的长度为n-2的Prufer序列和n个点的无根树一一对应，故n个点的无根树数量为$n^{n-2}$（Prufer序的每一位可以是1~n），这也是n个点的完全图的生成树个数。

②指定点度的无根树计数：如果要求点度序列是$D_1,D_2,...,D_n$（有解必须满足和为2n-2和除非n=1否则度不为0），那相当于把n-2个数排列后进行消序，即$\frac{(n-2)!}{(D_1-1)!...(D_n-1)!}$。

例题：BZOJ 1211: [HNOI2004]树的计数（这题要注意中间答案可能爆，要分解素因数上下减然后再乘起来）

例题：BZOJ 1005 明明的烦恼。（n个点指定度数，m个点未知。先将剩余度数视为同一个数，然后内部再任意分配m^left）