新年的新航线
statement
舒克和贝塔成立了一家航空公司。因为新年的来临,舒克贝塔打算重新规划航空路线。
舒克和贝塔的航空公司控制了 \(n\) 个机场,这 \(n\) 个机场的位置在地图上可看做一个正 \(n\) 边形的 \(n\) 个顶点,按顺时针依次编号为 \(1, \dots, n\)。
舒克和贝塔的航空公司掌握着这 \(n\) 个机场间的 \(2n-3\) 条双向航线,且他们恰好构成了这个正 \(n\) 边形的所有边和一个三角剖分。也即,如果把机场作为点,航线作为线画在地图上,那么我们可以看到这些航线只可能在端点处相交,且最外围的航线构成了那个正 \(n\) 边形的边,而正 \(n\) 边形内部被其他航线完全分成了一个个三角形。
新年来了,航空公司人员纷纷放假,所以舒克希望新规范的航线图,航线尽量少,但要保证乘客能从原来的航线图的任何两个地方往返(也就是说你希望找一棵原图的生成树)。
同时,为了提高运力,贝塔希望新规范的航线图,不存在一个机场恰好能和两个机场直接通过航线相连(也就是说任何一个节点的度数不为 \(2\))。
此外,受到航空管制的影响,你不能额外申请航线,只能取消部分航线。
现在它们找到了跳蚤,希望能帮助它们找出一个合法的方案。
sol
为什么三角剖分图里面是 \(n - 3\) 条边?
假设是 \(x\) 条边,思考一条一条加入的过程可知图里面有 \(x + 1\) 个三角形。
依据边数「算两次」列出方程:\(3(x + 1) = 2x + n\)。
所以 \(x = n - 3\)。
注意到:
假设是 \(x\) 条边,思考一条一条加入的过程可知图里面有 \(x + 1\) 个三角形。
所以其实三角剖分作为平面图的对偶图是树,并且是二叉树。
构建这棵树需要不断删掉二度点,实际上本题可以不显式建树。
构造
Part1
下图结构为原图的部分,\((5, 6)\) 是树上的边,实际不存在,其中 \(6\) 是树的叶子。
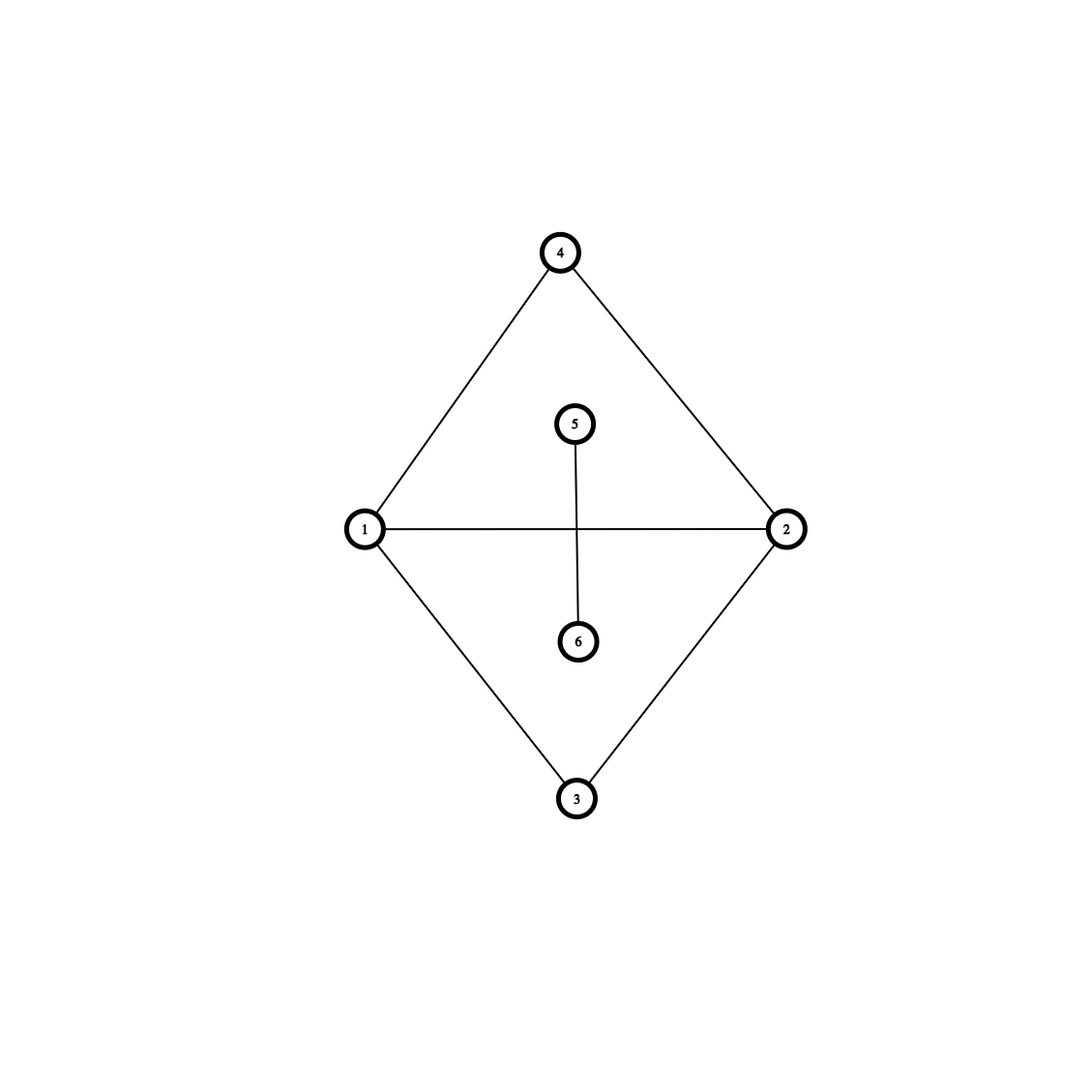
考虑删掉点 \(3\) 和 \(2\),如下构造,选择 \((1, 3)\) 和 \((1, 2)\) 作为生成树的边。
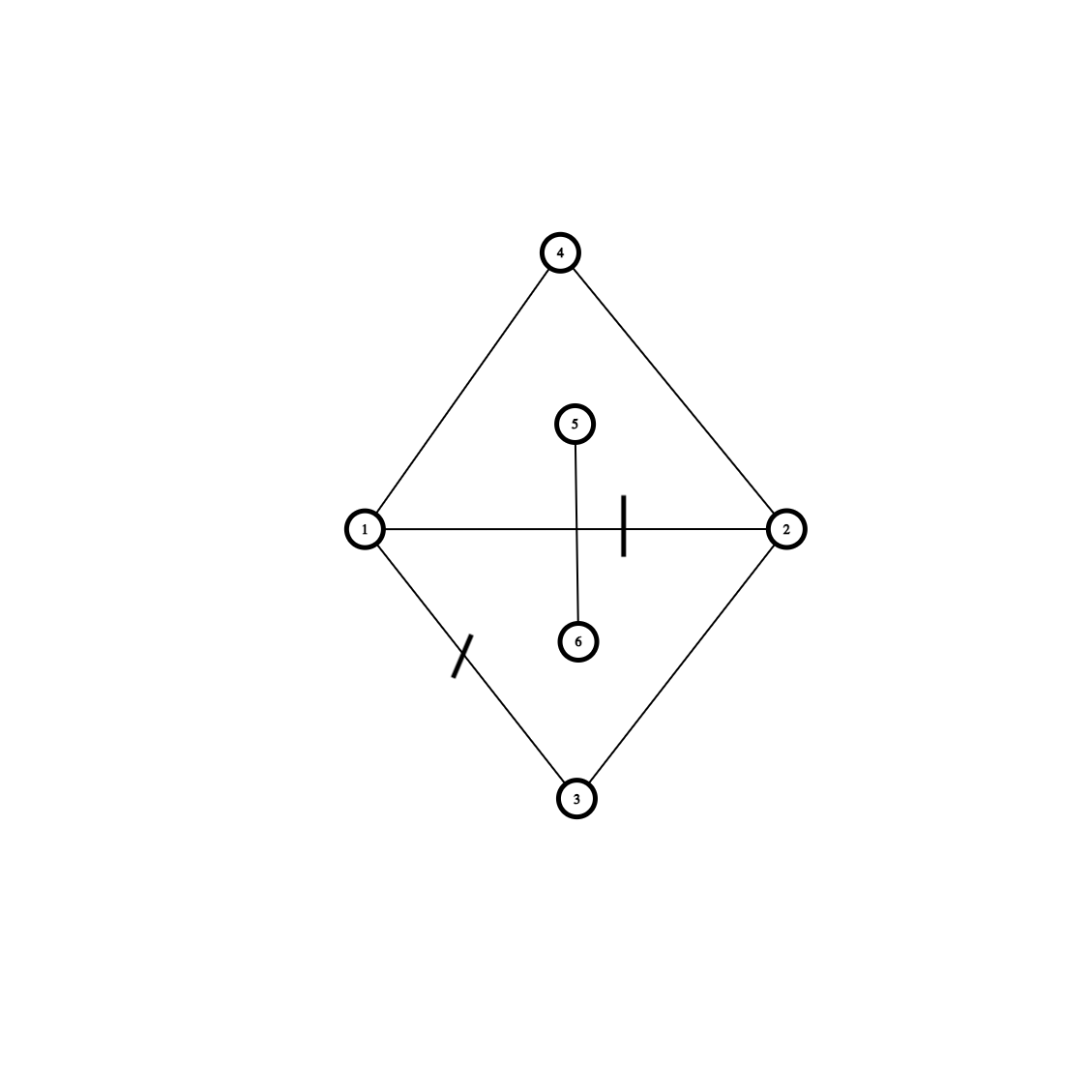
删去 \(3\) 和 \(2\) 后剩下的图中 \(1\) 和 \(4\) 度数都是大于 \(1\) 但不为 \(2\) 的,同时保证了 \(3\) 和 \(2\) 的度数合法,故这是可行的。
Part2
下图是另一结构,\(6, 7, 8\) 是树上的点,且 \(6, 7\) 是叶子。
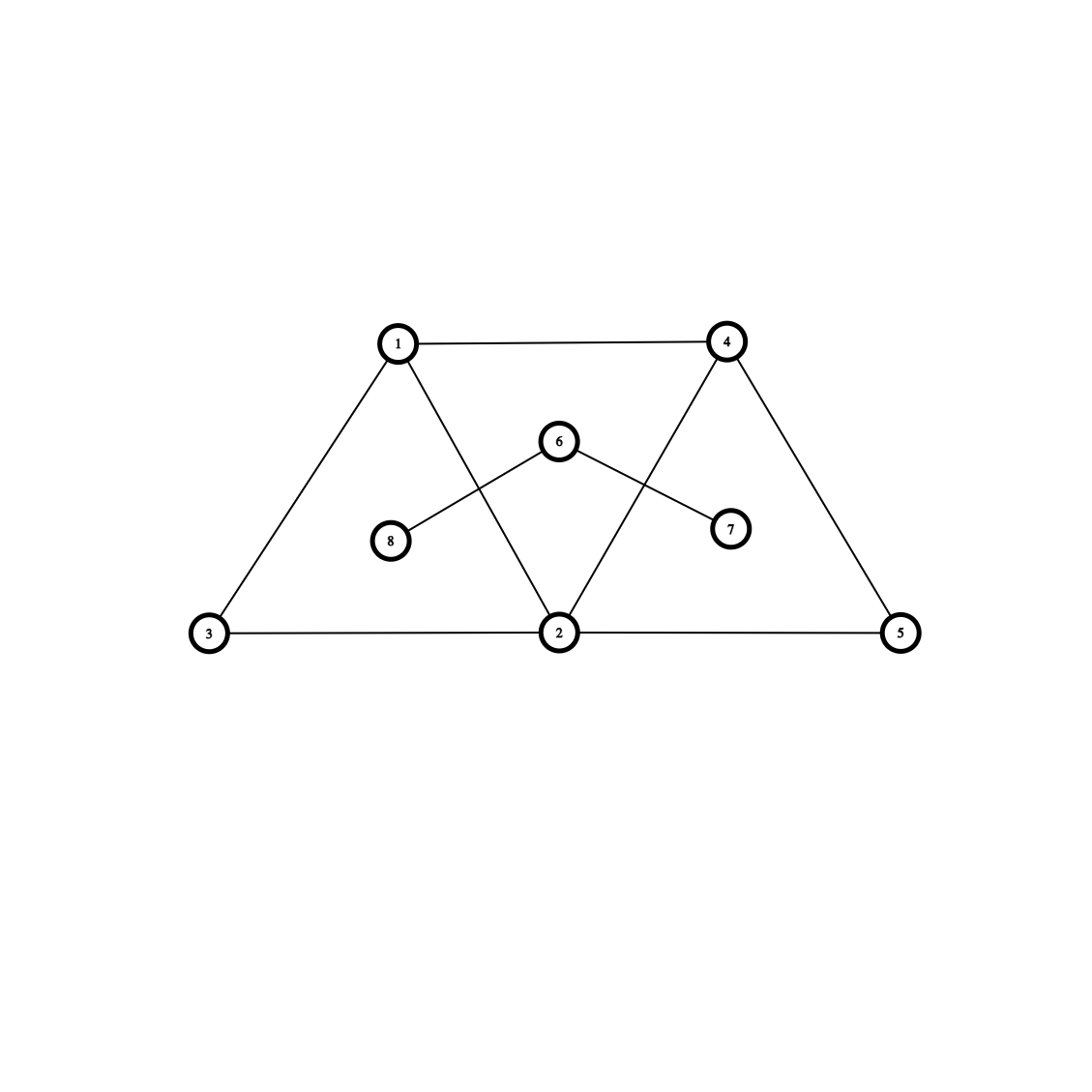
考虑删掉 \(3, 5\),如下构造,选择 \((3, 2)\) 和 \((2, 5)\) 即可。

容易检验构造的合法性,每个点最终都不是二度的。
Part3
最后如何实现删点,一个简单的做法是每次删叶子。
- 如果当前叶子两侧没有缩起来的三角形,就把改叶子对应的三角形缩起来。
- 如果当前叶子一侧没有缩起来的三角形,如 Part1 构造可以删去。
- 如果当前叶子两侧都有缩起来的三角形,如 Part2 构造,先删去两侧的三角形再回到第一种情况。
注意到边界情况是 \(4\) 个点的图,此时删二度点没有意义,因为无法把未满足限制的点交给下一次删点处理。
因为点数少,爆搜或讨论即可。
容易知道 \(n = 3\) 时恰好无解,其余的均有解,事实上边界情况是一定有解的。
构造本身说明正确性。
dp
原理简单明了,做树形 dp,记录点的度数信息转移,输出方案容易得到。
转移讨论 \(2\) 选 \(1\) 作为生成树的边。
注意边界情况是根的转移要选 \(2\) 条边。
实现
构造
#include <bits/stdc++.h>
using namespace std;
constexpr int N = 5e5 + 5;
int n;
set<int> e[N];
vector<int> ans[N];
map<int, int> tag[N];
queue<int> Q;
void link(int u, int v) {
e[u].insert(v);
e[v].insert(u);
}
void cut(int u, int v) {
e[u].erase(v);
e[v].erase(u);
}
void update(int u) {
if (e[u].size() == 2) {
Q.push(u);
}
}
void mark(int u, int v, int w) {
tag[u][v] = tag[v][u] = w;
}
void clear(int u, int v) {
tag[u][v] = tag[v][u] = 0;
}
void fixed(int u, int v) {
ans[u].push_back(v);
ans[v].push_back(u);
}
struct Dsu {
int cnt;
vector<int> fa;
Dsu(int n, int x) {
init(n, x);
}
void init(int n, int x) {
cnt = x;
fa.assign(n + 5, 0);
for (int i = 1; i <= n; i++) {
fa[i] = i;
}
}
int find(int x) {
if (x == fa[x]) {
return x;
} else {
return fa[x] = find(fa[x]);
}
}
bool merge(int x, int y) {
if (find(x) == find(y)) {
return 0;
}
fa[find(x)] = find(y);
cnt--;
return 1;
}
};
int main() {
cin >> n;
for (int i = 1; i < n; i++) {
link(i, i + 1);
}
link(n, 1);
for (int i = 1; i <= n - 3; i++) {
int u, v;
cin >> u >> v;
link(u, v);
}
if (n == 3) {
cout << "-1\n";
return 0;
}
for (int i = 1; i <= n; i++) {
if (e[i].size() == 2) {
Q.push(i);
}
}
for (int T = 1; T <= n - 4; T++) {
int u = Q.front();
Q.pop();
int i = *e[u].begin(), j = *next(e[u].begin());
int k = tag[u][i], l = tag[u][j];
if (k == 0 && l != 0) {
swap(i, j), swap(k, l);
}
if (k == 0 && l == 0) {
mark(i, j, u);
} else if (k != 0 && l == 0) {
fixed(k, i), fixed(u, i);
} else {
fixed(u, k), fixed(u, l);
mark(i, j, u);
}
cut(u, i), cut(u, j);
clear(u, i), clear(u, j);
update(i), update(j);
}
vector<pair<int, int>> edge;
for (int i = 1; i <= n; i++) {
for (int j : e[i]) {
if (i < j) {
edge.emplace_back(i, j);
}
}
for (auto [j, k] : tag[i]) {
if (i < j && k != 0) {
edge.emplace_back(i, k);
edge.emplace_back(j, k);
}
}
}
int m = edge.size();
int cnt = 0;
set<int> tmp;
for (int i = 0; i < m; i++) {
tmp.insert(edge[i].first);
tmp.insert(edge[i].second);
}
cnt = tmp.size();
for (int i = 0; i < 1 << m; i++) {
Dsu dsu(n, cnt);
bool flag = 1;
vector<int> deg(n + 5, 0);
for (int j = 0; j < m && flag; j++) {
if (i >> j & 1) {
if (dsu.merge(edge[j].first, edge[j].second)) {
deg[edge[j].first]++;
deg[edge[j].second]++;
} else {
flag = 0;
}
}
}
if (dsu.cnt != 1) {
flag = 0;
}
for (int i = 1; i <= n && flag; i++) {
if (deg[i] == 2) {
flag = 0;
}
}
if (flag) {
for (int j = 0; j < m; j++) {
if (i >> j & 1) {
fixed(edge[j].first, edge[j].second);
}
}
break;
}
}
for (int i = 1; i <= n; i++) {
for (int j : ans[i]) {
if (i < j) {
cout << i << " " << j << "\n";
}
}
}
return 0;
}
dp
见 yxh。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号