P2154 [SDOI2009]虔诚的墓主人
$ \color{#0066ff}{ 题目描述 }$
小W是一片新造公墓的管理人。公墓可以看成一块N×M的矩形,矩形的每个格点,要么种着一棵常青树,要么是一块还没有归属的墓地。
当地的居民都是非常虔诚的基督徒,他们愿意提前为自己找一块合适墓地。为了体现自己对主的真诚,他们希望自己的墓地拥有着较高的虔诚度。
一块墓地的虔诚度是指以这块墓地为中心的十字架的数目。一个十字架可以看成中间是墓地,墓地的正上、正下、正左、正右都有恰好k棵常青树。
小W希望知道他所管理的这片公墓中所有墓地的虔诚度总和是多少。
\(\color{#0066ff}{输入格式}\)
输入文件religious.in的第一行包含两个用空格分隔的正整数N和M,表示公墓的宽和长,因此这个矩形公墓共有(N+1) ×(M+1)个格点,左下角的坐标为(0, 0),右上角的坐标为(N, M)。
第二行包含一个正整数W,表示公墓中常青树的个数。
第三行起共W行,每行包含两个用空格分隔的非负整数xi和yi,表示一棵常青树的坐标。输入保证没有两棵常青树拥有相同的坐标。
最后一行包含一个正整数k,意义如题目所示。
\(\color{#0066ff}{输出格式}\)
输出文件religious.out仅包含一个非负整数,表示这片公墓中所有墓地的虔诚度总和。为了方便起见,答案对2,147,483,648取模。
\(\color{#0066ff}{输入样例}\)
5 6
13
0 2
0 3
1 2
1 3
2 0
2 1
2 4
2 5
2 6
3 2
3 3
4 3
5 2
2
\(\color{#0066ff}{输出样例}\)
6
\(\color{#0066ff}{数据范围与提示}\)
6
说明
图中,以墓地(2, 2)和(2, 3)为中心的十字架各有3个,即它们的虔诚度均为3。其他墓
地的虔诚度为0。
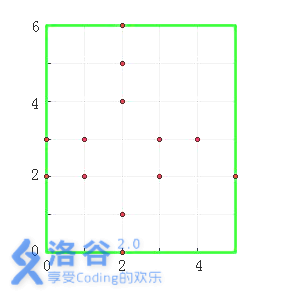
对于30%的数据,满足1 ≤ N, M ≤ 1,000。
对于60%的数据,满足1 ≤ N, M ≤ 1,000,000。
对于100%的数据,满足1 ≤ N, M ≤ 1,000,000,000,0 ≤ xi ≤ N,0 ≤ yi ≤ M,1 ≤ W ≤ 100,000,1 ≤ k ≤ 10。
存在50%的数据,满足1 ≤ k ≤ 2。
存在25%的数据,满足1 ≤ W ≤ 10000。
\(\color{#0066ff}{题解}\)
一个点的贡献是\(C_{上面点的个数}^k*C_{下面点的个数}^k*C_{左面点的个数}^k*C_{右面点的个数}^k\)
把所有点按x为第一关键字,y为第二关键字从大到小排序
然后枚举x,对于两个x相同的y,直接的贡献中,上下的那部分是不变的
我们只需统计中间这些点中的左右贡献之和即可
而贡献取决于点数,所以在按顺序扫的时候,我们可以开一个map动态知道左右两边的点数
然后用一个动态开点的权值线段树,支持区间查询单点修改,即可解决本题
发现k极小,可以把组合数暴力预处理(模拟约分)
// luogu-judger-enable-o2
#include<bits/stdc++.h>
#define LL long long
LL in() {
char ch; LL x = 0, f = 1;
while(!isdigit(ch = getchar()))(ch == '-') && (f = -f);
for(x = ch ^ 48; isdigit(ch = getchar()); x = (x << 1) + (x << 3) + (ch ^ 48));
return x * f;
}
const LL mod = 2147483648;
const int maxn = 1e5 + 10;
LL w, k, n, m;
LL c[maxn];
std::map<LL, LL> pre, nxt;
std::pair<LL, LL> mp[maxn];
struct Tree {
protected:
struct node {
node *ch[2];
LL val;
node(LL val = 0): val(val) { ch[0] = ch[1] = NULL; }
void upd() { val = ((ch[0]? ch[0]->val : 0) + (ch[1]? ch[1]->val : 0)) % mod; }
}*root, *tail, pool[maxn << 2];
void add(node *&o, int l, int r, int pos, LL k) {
if(!o) o = new(tail++) node();
if(l == r) return (void)(o->val = k);
int mid = (l + r) >> 1;
if(pos <= mid) add(o->ch[0], l, mid, pos, k);
else add(o->ch[1], mid + 1, r, pos, k);
o->upd();
}
LL query(node *o, int l, int r, int x, int y) {
if(!o) return 0;
if(x <= l && r <= y) return o->val;
int mid = (l + r) >> 1;
LL ans = 0;
if(x <= mid) (ans += query(o->ch[0], l, mid, x, y)) %= mod;
if(y > mid) (ans += query(o->ch[1], mid + 1, r, x, y)) %= mod;
return ans;
}
public:
Tree() { tail = pool; }
void add(int pos, LL k) { add(root, 0, m, pos, k); }
LL query(int l, int r) { return query(root, 0, m, l, r); }
}s;
LL gcd(LL x, LL y) { return y? gcd(y, x % y) : x; }
void getC() {
static LL b[22];
for(int i = k; i <= w; i++) {
c[i] = 1;
for(int a = 1; a <= k; a++) b[a] = a;
for(int a = i - k + 1; a <= i; a++) {
int now = a;
for(int v = 2; v <= k; v++) {
int gc = gcd(b[v], now);
now /= gc;
b[v] /= gc;
}
c[i] = (1LL * c[i] * now) % mod;
}
}
}
void work() {
LL ans = 0;
getC();
std::sort(mp + 1, mp + w + 1);
for(int i = w; i >= 1; i--) nxt[mp[i].second]++;
for(int i = 1; i <= w; i++) {
int pos = i;
while(pos <= w && mp[pos].first == mp[i].first) pos++;
pos--;
for(int j = i; j < pos; j++) (ans += c[j - i + 1] * c[pos - j] % mod * s.query(mp[j].second + 1, mp[j + 1].second - 1) % mod) %= mod;
for(int j = i; j <= pos; j++) {
nxt[mp[j].second]--;
pre[mp[j].second]++;
s.add(mp[j].second, 1LL * c[pre[mp[j].second]] * c[nxt[mp[j].second]] % mod);
}
i = pos;
}
printf("%lld", ans);
}
signed main() {
n = in(), m = in(), w = in();
LL x, y;
for(int i = 1; i <= w; i++) x = in(), y = in(), mp[i] = std::make_pair(x, y);
k = in();
work();
return 0;
}
----olinr


 浙公网安备 33010602011771号
浙公网安备 33010602011771号